Trang chủ Toán 11

Bài tập 3 trang 97 SGK Đại số & Giải tích 11

Lý thuyết18 Trắc nghiệm

5 BT SGK

28 FAQ

Giải bài 3 tr 97 sách GK Toán ĐS & GT lớp 11

Trong các bài toán về cấp số cộng, ta thường gặp năm đại lượng \(u_1, n, d, u_n, S_n.\)

a) Hãy viết các hệ thức liên hệ giữa các đại lượng để có thể tìm được các đại lượng còn lại?

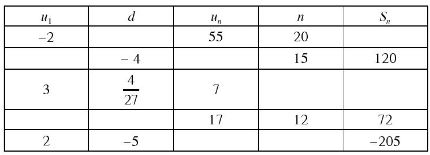
b) Lập bảng theo mẫu sau và điền vào chỗ trống thích hợp:

 

Hướng dẫn giải chi tiết bài 3

Câu a:

Các hệ thức liên hệ giữa các đại lượng u1, d, n, un, Sn.

\(u_n=u_1+(n-1)d\) với \(n\geq 2\)

\(S_n=\frac{n(n_1+u_n)}{2}=nu_1+\frac{n(n-1)}{2}d\)

Phải biết ít nhất ba đại lượng trong năm đại lượng nói trên để tính được các đại lượng còn lại.

Câu b:

Thực chất đây là năm bài tập nhỏ, mỗi bài ứng với các dữ liệu ở một dòng. Học sinh phải giải từng bài nhỏ rồi mới điền kết quả.

Hàng 1: Biết u1 = -2, un = 55, n = 20. Tìm d, Sn    

Áp dụng công thức \(d=\frac{u_n-u_1}{n-1}\),\(S_n=\frac{(u_1+u_n).n}{2}\)

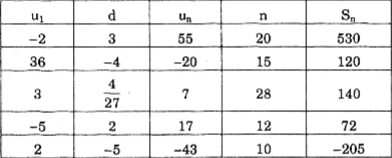
Đáp số: d = 3, S20 = 530.

Hàng 2: Biết d = -4, n = 15, Sn = 120. Tìm u1, un

Áp dụng công thức un = u1 + (n - 1)d và \(S_n=\frac{(u_1+u_n).n}{2}\),

ta có: 

Giải hệ trên, ta được u1 = 36, u15 = - 20.

Tuy nhiên, nếu sử dụng công thức 

thì S15 = 120 = 15u1 + .

Từ đó ta có u1 = 36 và tìm được u15 = - 20.

Hàng 3: Áp dụng công thức un = u1 + (n - 1)d, từ đây ta tìm được n; tiếp theo áp dụng công thức \(S_n=\frac{(u_1+u_n).n}{2}\). Đáp số: n = 28, Sn = 140.

Hàng 4: Áp dụng công thức \(S_n=\frac{(u_1+u_n).n}{2}\), từ đây tìm được n, tiếp theo áp dụng công thức un = u1 + (n - 1)d. Đáp số: u1 = -5, d= 2.

Hàng 5: Áp dụng công thức \(S_n=\frac{\left [ 2u_1+(2-1)d \right ].n}{2}\), từ đây tìm được n, tiếp theo áp dụng công thức un = u1 + (n - 1)d. Đáp số: n = 10, un = -43

-- Mod Toán 11 HỌC247

Video hướng dẫn giải bài 3 SGK

Nếu bạn thấy hướng dẫn giải Bài tập 3 trang 97 SGK Đại số & Giải tích 11 HAY thì click chia sẻ 

Để luyện tập thêm dạng bài tương tự như Bài tập 3 trang 97 trong SGK các em làm thêm câu hỏi trắc nghiệm sau để cũng cố kỹ năng làm dạng bài.

  • Câu 1:

    Cho các cấp số cộng có các số hạng lần lượt là 5;9;13;17;... Khi đó un được tính theo biểu thức nào dưới đây?

    • A. un=5n+1
    • B. un=5n-1
    • C. un=4n+1
    • D. un=4n-1

Được đề xuất cho bạn