Bài tập 20 trang 114 SGK Toán 11 NC
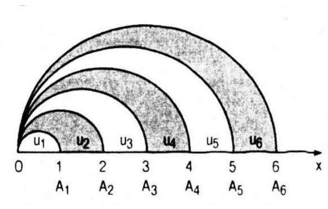
Trên tia Ox lấy ác điểm A1, A2, …, An,… sao cho mỗi số nguyên dương n, OAn = n. Trong cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia Ox, vẽ các nửa đường tròn đường kính OAn, n= 1,2,… Kí hiệu là diện tích của nửa hình tròn đường kính OA1 và với mỗi n ≥ 2, kí hiệu un là diện tích của hình giới hạn bởi nửa đường tròn đường kính OAn -1 , nửa đường tròn đường kính OAn và tia Ox. Chứng minh rằng dãy số (un) là một cấp số cộng. Hãy xác định công sai của cấp số cộng đó.
Hướng dẫn giải chi tiết
Với \(n \ge 2\), ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
{u_n} = \frac{1}{2}\left( {\pi \frac{{OA_n^2}}{4} - \pi \frac{{OA_{n - 1}^2}}{4}} \right)\\
= \frac{1}{2}\pi \left[ {\left( {{n^2} - {{\left( {n - 1} \right)}^2}} \right)} \right]\\
= \frac{{\left( {2n - 1} \right)\pi }}{8}\left( {n \ge 2} \right)
\end{array}\\
\begin{array}{l}
\Rightarrow {u_{n + 1}} - {u_n} = \frac{{2n + 1}}{8}\pi - \frac{{\left( {2n - 1} \right)}}{8}\pi \\
= \frac{\pi }{4},\forall n \ge 2
\end{array}
\end{array}\)
Mặt khác:
\({u_2} - {u_1} = \frac{{3\pi }}{8} - \frac{\pi }{8} = \frac{\pi }{4}\)
Vậy \({u_{n + 1}} - {u_n} = \frac{\pi }{4},\forall n \in {N^*}\)
Do đó \(\left( {{u_n}} \right)\) là cấp số cộng với công sai \(d = \frac{\pi }{4}\).
-- Mod Toán 11 HỌC247
-


Tìm u1 và d biết u3+u5+u7=45 và (u4)^2-(u2)^2=108
bởi Kiều Oanh
 15/12/2019
Giúp hộ mình với ạ
15/12/2019
Giúp hộ mình với ạ Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 Cấp số cộng và xác suất biến cố
Cấp số cộng và xác suất biến cố Theo dõi (1) 6 Trả lời
Theo dõi (1) 6 Trả lời -


Tìm u1 và d biết u2=1/4 và u5=16
bởi Honnun Bùi
 12/12/2019
U2=1/4 và u5=16.tìm u1 và d giải thích robràng vớiTheo dõi (1) 3 Trả lời
12/12/2019
U2=1/4 và u5=16.tìm u1 và d giải thích robràng vớiTheo dõi (1) 3 Trả lời -


Nêu cách tìm d trong cấp số cộng
bởi Trung Hậu
 12/12/2019
Cách tìm d trong cấp số cộngTheo dõi (0) 2 Trả lời
12/12/2019
Cách tìm d trong cấp số cộngTheo dõi (0) 2 Trả lời -

 Khi d>0. Ta được cấp số cộng là1 dãy số như thế nàoTheo dõi (0) 0 Trả lời
Khi d>0. Ta được cấp số cộng là1 dãy số như thế nàoTheo dõi (0) 0 Trả lời -


Tính xác suất 3 lần gieo con súc sắc đều mặt lẻ
bởi Thanh Pham
 10/12/2019
Giải tu luan ra nha
10/12/2019
Giải tu luan ra nha Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời