Giải bài 5 tr 98 sách GK Toán Hình lớp 11
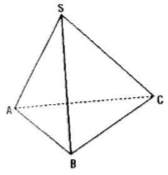
Cho hình chóp tam giác S.ABC có SA = SB = SC và có \(\widehat{ABC}= \widehat{BSC}=\widehat{CSA}.\) Chứng minh rằng SA ⊥ BC, SB ⊥ AC, SC ⊥ AB.
Hướng dẫn giải chi tiết bài 5
\(\overrightarrow{SA}.\overrightarrow{BC}=\overrightarrow{SA}.(\overrightarrow{SC}-\overrightarrow{SB})\)
\(=\overrightarrow{SA}.\overrightarrow{SC}-\overrightarrow{SA}.\overrightarrow{SB}\)
\(= SA.SC.\cos\widehat{ASC} - SA.SB.\cos\widehat{ASB} = 0\)
Vậy \(SA ⊥ BC\).
\(\overrightarrow{SB}.\overrightarrow{AC}=\overrightarrow{SB}.(\overrightarrow{SC}-\overrightarrow{SA})\)
\(=\overrightarrow{SB}.\overrightarrow{SC}-\overrightarrow{SB}.\overrightarrow{SA}\)
\(= SB.SC.\cos\widehat{BSC} - SB.SA.\cos\widehat{ASB} = 0\)
Vậy \(SB ⊥ AC\).
\(\overrightarrow{SC}.\overrightarrow{AB}=\overrightarrow{SC}.(\overrightarrow{SB}-\overrightarrow{SA})\)
\(=\overrightarrow{SC}.\overrightarrow{SB}-\overrightarrow{SC}.\overrightarrow{SA}\)
\(= SC.SB.\cos\widehat{BSC} - SC.SA.\cos\widehat{ASC} = 0\)
Vậy \(SC ⊥ AB\)
-- Mod Toán 11 HỌC247
Video hướng dẫn giải bài 5 SGK
-


Cho hình chóp SABCD có đáy ABCD là hình chữ nhật, có SA vuông góc AD. a) Cm CD vuông góc SD
bởi Đặng Cẩm Vân
 06/02/2021
06/02/2021
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật, có SA vuông góc AD
a) Cm CD vuông góc SD
b) Cm CB vuông góc SB
c) Cho AH vuông góc SD, AK vuông góc SB. Cm SC vuông góc HK
Theo dõi (0) 0 Trả lời -


Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a với SA = SB = SC = 2a, gọi O = AC giao BD. tính góc giữa SA và BC, tính góc giữa SA và CD. gọi M là trung điểm của BC tính góc giữa BM và AD. chứng minh SO vuông góc với AB tính góc giữa SD và AC
bởi Thiệu Bảo Quân
 29/01/2021
29/01/2021
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


A. Nếu a // b và b // c thì a //c.
B. Nếu a vuông góc với b ; b vuông góc với c thì a // c.
C. Cho a // b. Nếu a vuông góc với c thì b vuông góc với c.
D. Hai đường thẳng vuông góc với nhau thì tích vô hướng của hai vecto chỉ phương của hai đường thẳng đó bằng 0.
Theo dõi (0) 1 Trả lời -


A. Song song với nhau
B. Vuông góc với nhau.
C. Chéo nhau
D. Tất cả sai.
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 3 trang 97 SGK Hình học 11
Bài tập 4 trang 98 SGK Hình học 11
Bài tập 6 trang 98 SGK Hình học 11
Bài tập 7 trang 98 SGK Hình học 11
Bài tập 8 trang 98 SGK Hình học 11
Bài tập 3.8 trang 138 SBT Hình học 11
Bài tập 3.9 trang 138 SBT Hình học 11
Bài tập 3.10 trang 138 SBT Hình học 11
Bài tập 3.11 trang 139 SBT Hình học 11
Bài tập 3.12 trang 139 SBT Hình học 11
Bài tập 3.13 trang 139 SBT Hình học 11
Bài tập 3.14 trang 139 SBT Hình học 11
Bài tập 3.15 trang 139 SBT Hình học 11
Bài tập 7 trang 95 SGK Hình học 11 NC
Bài tập 8 trang 95 SGK Hình học 11 NC
Bài tập 9 trang 96 SGK Hình học 11 NC






