Giải bài 3.8 tr 138 SBT Hình học 11
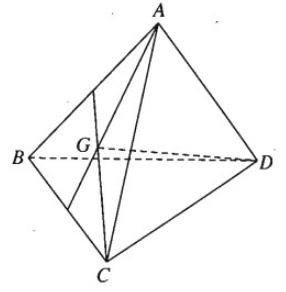
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng:
\(\overrightarrow {GD} .\overrightarrow {GA} + \overrightarrow {GD} .\overrightarrow {GB} + \overrightarrow {GD} .\overrightarrow {GC} = 0\)
Hướng dẫn giải chi tiết
Ta có:
\(\overrightarrow {GD} .\overrightarrow {GA} + \overrightarrow {GD} .\overrightarrow {GB} + \overrightarrow {GD} .\overrightarrow {GC} = \overrightarrow {GD} \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) = \overrightarrow {GD} .\overrightarrow 0 = 0\)
(Vì G là trọng tâm của tam giác ABCD nên \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \))
-- Mod Toán 11 HỌC247
-
Chứng minh \(HK \bot BC\)?
bởi Trần Thị Vi
05/06/2020
giải toán hình
Theo dõi (0) 0 Trả lời -
Góc giữa AM và BD bằng?
bởi Trang Minh
03/06/2020
Cho hình chóp SABCD có ABCD là hình vuông cạnh a cạnh bên SA vuông gics với mặt phẳng đáy SA=a gọi M là trung điểm của SB góc giữa AM, BD
Theo dõi (0) 0 Trả lời -
Tính góc giữa MN và (SAC)?
bởi Bích Dung
29/05/2020
Bài 6
Theo dõi (0) 0 Trả lời -
Chứng minh AH vuông góc (BCD)?
bởi Trần Thu Hải
20/05/2020
Làm giúp mình câu 9 với ạ
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 7 trang 98 SGK Hình học 11
Bài tập 8 trang 98 SGK Hình học 11
Bài tập 3.9 trang 138 SBT Hình học 11
Bài tập 3.10 trang 138 SBT Hình học 11
Bài tập 3.11 trang 139 SBT Hình học 11
Bài tập 3.12 trang 139 SBT Hình học 11
Bài tập 3.13 trang 139 SBT Hình học 11
Bài tập 3.14 trang 139 SBT Hình học 11
Bài tập 3.15 trang 139 SBT Hình học 11
Bài tập 7 trang 95 SGK Hình học 11 NC
Bài tập 8 trang 95 SGK Hình học 11 NC
Bài tập 9 trang 96 SGK Hình học 11 NC
