Giải bài 3.10 tr 138 SBT Hình học 11
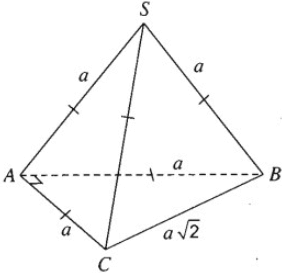
Cho hình chóp tam giác S.ABC có SA = SB = SC = AB = AC = a và \(BC = a\sqrt 2 \). Tính góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {SC} \).
Hướng dẫn giải chi tiết
Ta tính côsin của góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {SC} \). Ta có
\(\begin{array}{l}
\cos \left( {\overrightarrow {SC} ,\overrightarrow {AB} } \right) = \frac{{\overrightarrow {SC} .\overrightarrow {AB} }}{{\left| {\overrightarrow {SC} } \right|.\left| {\overrightarrow {AB} } \right|}} = \frac{{\left( {\overrightarrow {SA} + \overrightarrow {AC} } \right).\overrightarrow {AB} }}{{{a^2}}}\\
= \frac{{\overrightarrow {SA} .\overrightarrow {AB} + \overrightarrow {AC} .\overrightarrow {AB} }}{{{a^2}}}
\end{array}\)
Theo giả thiết ta suy ra hình chóp có các tam giác đều là SAB, SAC và các tam giác vuông là ABC vuông tại A và SBC vuông tại S.
Do đó \(\overrightarrow {SA} .\overrightarrow {AB} = a.a.\cos {120^0} = - \frac{{{a^2}}}{2}\) và \({\overrightarrow {AC} .\overrightarrow {AB} = 0}\)
Vậy \(\cos \left( {\overrightarrow {SC} ,\overrightarrow {AB} } \right) = - \frac{1}{2}\) hay \(\left( {\overrightarrow {SC} ,\overrightarrow {AB} } \right) = {120^0}\)
Vậy góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {SC} \) bằng 120o.
-- Mod Toán 11 HỌC247
-


Tính cos góc hợp bởi SC và (SBD) biết hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông với (ABCD), AB=a, SA=a căn3, BC=a căn2
bởi anhdaden
 04/04/2020
Cho hình chóp S.ABCD có đáy là hình chữ nhật. SA vuông với (ABCD), AB=a, SA=a căn3, BC=a căn2. Tính cos góc hợp bởi SC và (SBD)Theo dõi (0) 0 Trả lời
04/04/2020
Cho hình chóp S.ABCD có đáy là hình chữ nhật. SA vuông với (ABCD), AB=a, SA=a căn3, BC=a căn2. Tính cos góc hợp bởi SC và (SBD)Theo dõi (0) 0 Trả lời -


Tính cos góc hợp bởi SC và (SBD) biết hình chóp S.ABCD có đáy là hình chữ nhật
bởi anhdaden
 04/04/2020
Cho hình chóp S.ABCD có đáy là hình chữ nhật. SA vuông với (ABCD), AB=a, SA=a căn3, BC=a căn2. Tính cos góc hợp bởi SC và (SBD)Theo dõi (0) 0 Trả lời
04/04/2020
Cho hình chóp S.ABCD có đáy là hình chữ nhật. SA vuông với (ABCD), AB=a, SA=a căn3, BC=a căn2. Tính cos góc hợp bởi SC và (SBD)Theo dõi (0) 0 Trả lời -


Cho tứ diện ABCD, với AB vuông góc AC, AB vuông góc BD. Gọi P, Q lần lượt là trung điểm của AB và CD. Góc giữa PQ và AB là ?
bởi Ben Ben
 02/04/2020
02/04/2020
 Theo dõi (0) 7 Trả lời
Theo dõi (0) 7 Trả lời -


Cho tứ diện đều SABC và M, N, P lần lượt là trung điểm của BC, SA, SB. Tính góc giữa SM và BN, góc giữa SM và AP.
bởi Trương Thế Vinh
 28/03/2020
28/03/2020
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời
Bài tập SGK khác
Bài tập 3.8 trang 138 SBT Hình học 11
Bài tập 3.9 trang 138 SBT Hình học 11
Bài tập 3.11 trang 139 SBT Hình học 11
Bài tập 3.12 trang 139 SBT Hình học 11
Bài tập 3.13 trang 139 SBT Hình học 11
Bài tập 3.14 trang 139 SBT Hình học 11
Bài tập 3.15 trang 139 SBT Hình học 11
Bài tập 7 trang 95 SGK Hình học 11 NC
Bài tập 8 trang 95 SGK Hình học 11 NC
Bài tập 9 trang 96 SGK Hình học 11 NC