Giải bài 8 tr 98 sách GK Toán Hình lớp 11
Cho tứ diện ABCD có AB = AC = AD và \(\widehat{BAC}=\widehat{BAD}=60^{0}.\) Chứng minh rằng:
a) AB ⊥ CD;
b) Nếu M, N lần lượt là trung điểm của AB và CD thì MN ⊥ AB và MN ⊥ CD.
Hướng dẫn giải chi tiết bài 8
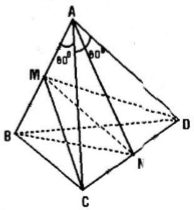
Câu a:
Xét tích vô hướng:
\(\overrightarrow{AB}.\overrightarrow{CD}= \overrightarrow{AB}.(\overrightarrow{AD}-\overrightarrow{AC})\)
\(=\overrightarrow{AB}.\overrightarrow{AD}- \overrightarrow{AB}.\overrightarrow{AC}\)
\(=\left |\overrightarrow{AB} \right |.\left |\overrightarrow{AD} \right |.cos\widehat{BAD} - \left |\overrightarrow{AB} \right |.\left |\overrightarrow{AC} \right |.cos \widehat{BAC}\)
\(=AB.AD.cos60^0-AB.AC.cos60^0 =0\) (Vì AB = AC = AD)
\(\Rightarrow AB\perp CD\) (đpcm).
Câu b:
Nhận thấy: tam giá ABC có AB = AC và \(\widehat{BAC}=60^0\Rightarrow\) tam giác ABC là tam giác đều ⇒ AB = BC = AC.
Tương tự cũng có tam giác ABD đều ⇒ AB = AD = BD.
\(\Rightarrow \Delta ACD=\Delta BCD\) (c.c.c) ⇒ các trung tuyến BN và AN bằng nhau.
\(\Rightarrow \Delta NAB\) cần đỉnh N mà M là tam giác cân đỉnh M mà N là trung điểm CD \(\Rightarrow MN\perp CD\)
Vậy \(MN\perp AB\) và \(MN\perp CD\) (đpcm).
-- Mod Toán 11 HỌC247
Video hướng dẫn giải bài 8 SGK
-
Mệnh đề nào đúng?
bởi Như Quỳnh
08/04/2020
Giúp mình giải bài này nha. Mình đang cần gấp. (Ghi rõ cách giải giúp mình nha)
Theo dõi (2) 1 Trả lời -
Tính cos góc hợp bởi SC và (SBD) biết hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông với (ABCD), AB=a, SA=a căn3, BC=a căn2
bởi anhdaden
04/04/2020
Cho hình chóp S.ABCD có đáy là hình chữ nhật. SA vuông với (ABCD), AB=a, SA=a căn3, BC=a căn2. Tính cos góc hợp bởi SC và (SBD)Theo dõi (0) 0 Trả lời -
Tính cos góc hợp bởi SC và (SBD) biết hình chóp S.ABCD có đáy là hình chữ nhật
bởi anhdaden
04/04/2020
Cho hình chóp S.ABCD có đáy là hình chữ nhật. SA vuông với (ABCD), AB=a, SA=a căn3, BC=a căn2. Tính cos góc hợp bởi SC và (SBD)Theo dõi (0) 0 Trả lời
