Bài tập 43 trang 47 SGK Toán 11 NC
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ?
a. Các hàm số y = sinx, y = cosx có cùng tập xác định.
b. Các hàm số y = tanx, y = cotx có cùng tập xác định.
c. Các hàm số y = sinx, y = tanx là những hàm số lẻ.
d. Các hàm số y = cosx, y = cotx là những hàm số chẵn.
e. Các hàm số y = sinx, y = cosx cùng nghịch biến trên khoảng \(\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\)
f. Hàm số y = cosx nghịch biến trên khoảng \(\left( { - 2\pi ; - \pi } \right)\)
g. Trên mỗi khoảng mà hàm số y = tanx đồng biến thì hàm số y = cotx nghịch biến.
Hướng dẫn giải chi tiết
a) Đúng vì hàm số y = sinx, y = cosx có cùng tập xác định D = R
b) Sai vì y = tanx xác định \(\forall x \ne \frac{\pi }{2} + k\pi \) còn y = cotx xác định ∀x ≠ kπ
c) Đúng
d) Sai vì y = cotx là hàm số lẻ.
e) Sai vì y = cosx không nghịch biến trên khoảng \(\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\)
f) Đúng
g) Sai vì trên khoảng \(\left( { - 2\pi ; - \pi } \right)\) hàm số y = tanx đồng biến nhưng hàm số y = cotx không nghịch biến.
-- Mod Toán 11 HỌC247
-


Tìm tất cả các giá trị thực của tham số m để phương trình cos2x – (2m + 1)cosx + m + 1 = 0 có nghiệm trên khoảng (π/2,3π/2).
bởi Suong dem
 24/01/2021
24/01/2021
A. -1 < m < 1.
B. -1 ≤ m <0.
C. -1 < m < 0.
D. -1 < m < 0.5.
Theo dõi (0) 1 Trả lời -


Tìm tất cả các giá trị thực của tham số m để phương trình tanx + mcotx = 8 có nghiệm.
bởi Nguyễn Trà Giang
 24/01/2021
24/01/2021
A. m > 16
B. m < 16
C. m = 16
D. m ≤ 16
Theo dõi (0) 1 Trả lời -


Tìm min, max của hàm số y=3/cosx 5?
bởi Bùi Đức Nam
 15/09/2020
y=3/cosx 5Theo dõi (0) 0 Trả lời
15/09/2020
y=3/cosx 5Theo dõi (0) 0 Trả lời -

 gtln và gtnn của hàm số lần lượt là y=1-4sin( x/2 pi/3 )Theo dõi (0) 0 Trả lời
gtln và gtnn của hàm số lần lượt là y=1-4sin( x/2 pi/3 )Theo dõi (0) 0 Trả lời -


Giải phương trình: cos2xsin2xcos4x=0
bởi viẹt phùng đình
 07/09/2020
Cos2xsin2xcos4x=0 có nghiệm làTheo dõi (0) 1 Trả lời
07/09/2020
Cos2xsin2xcos4x=0 có nghiệm làTheo dõi (0) 1 Trả lời -


Giải phương trình: cos4x = (√2 2cosx) (cos2x - sin2x)?
bởi Nguyễn Vi
 02/09/2020
Giải phương trình: cos4x = (√2 2cosx) (cos2x - sin2x)Theo dõi (0) 0 Trả lời
02/09/2020
Giải phương trình: cos4x = (√2 2cosx) (cos2x - sin2x)Theo dõi (0) 0 Trả lời -


Giải phương trình \(\sin 19x.\cos 21x=\sin 9x . \cos 11x\)?
bởi Kimie
 26/08/2020
26/08/2020
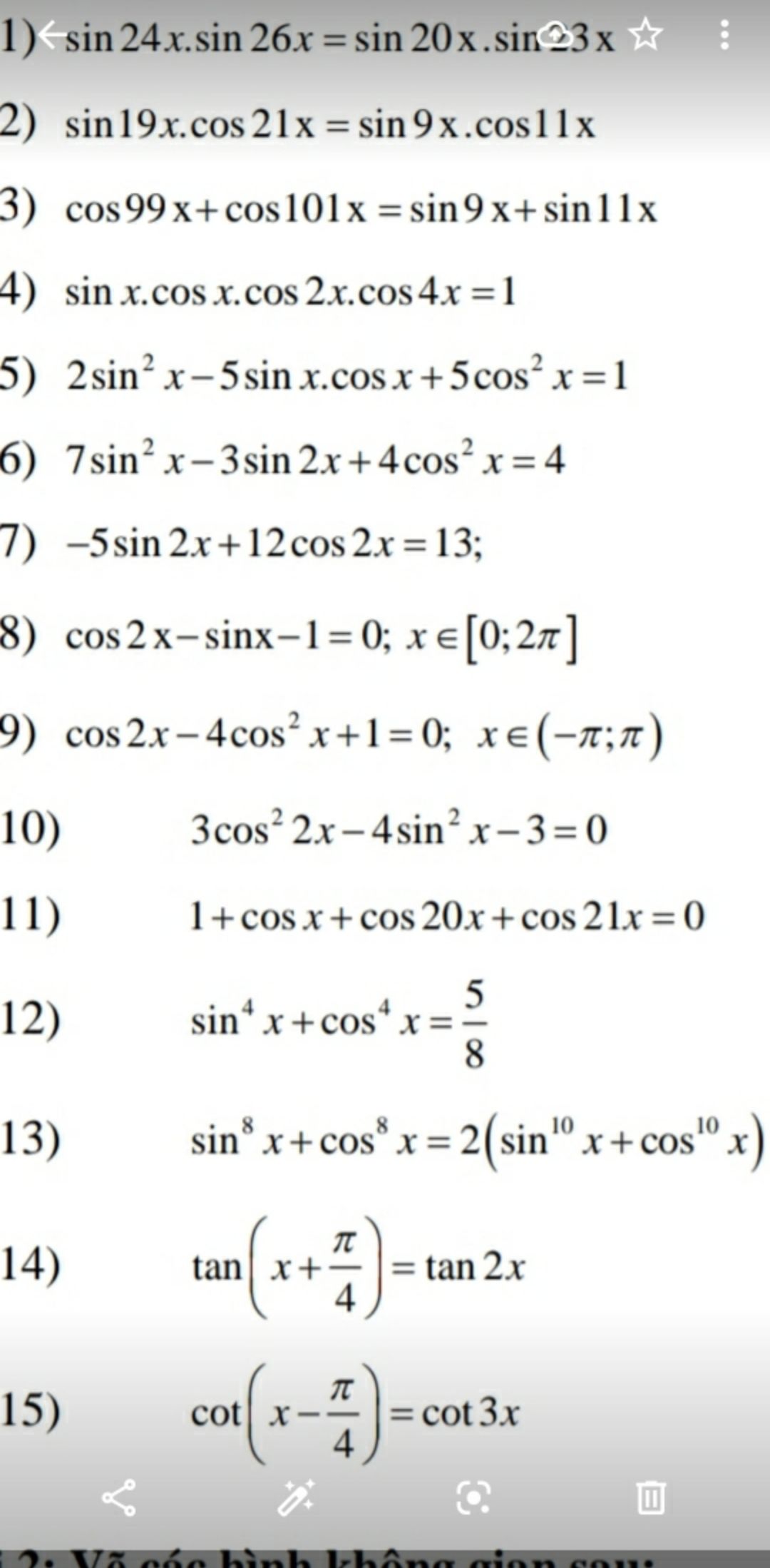 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình \({\sin ^3}x + {\rm{co}}{{\rm{s}}^3}x = \sin x - \cos x\)?
bởi Trần Thị Phương Thảo
 19/08/2020
19/08/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình \(\sin 2x-\cos 2x =\sqrt 2 \sin 3x \) với \( - \frac{\pi }{2} < x < \frac{{5\pi }}{2}\)?
bởi Trần Hùng Sơn
 18/08/2020
18/08/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 1.57 trang 41 SBT Toán 11
Bài tập 1.58 trang 41 SBT Toán 11
Bài tập 44 trang 47 SGK Toán 11 NC
Bài tập 45 trang 47 SGK Toán 11 NC
Bài tập 46 trang 48 SGK Toán 11 NC
Bài tập 47 trang 48 SGK Toán 11 NC
Bài tập 48 trang 48 SGK Toán 11 NC
Bài tập 49 trang 48 SGK Toán 11 NC
Bài tập 50 trang 48 SGK Toán 11 NC
Bài tập 51 trang 48 SGK Toán 11 NC
Bài tập 52 trang 48 SGK Toán 11 NC
Bài tập 53 trang 49 SGK Toán 11 NC
Bài tập 54 trang 49 SGK Toán 11 NC
Bài tập 55 trang 49 SBT Toán 11 NC
Bài tập 56 trang 49 SGK Toán 11 NC
Bài tập 57 trang 49 SGK Toán 11 NC
Bài tập 58 trang 49 SGK Toán 11 NC
Bài tập 59 trang 49 SGK Toán 11 NC
Bài tập 60 trang 49 SGK Toán 11 NC
Bài tập 61 trang 49 SGK Toán 11 NC





