Giải bài 3 tr 71 sách GK Toán Hình lớp 11
Cho hình hộp ABCD.A'B'C'D'
a) Chứng minh rằng hai mặt phẳng (BDA') và (B'D'C) song song với nhau.
b) Chứng minh rằng đường chéo AC' đi qua trọng tâm \({G_{1}, {G_{2}}^{}}^{}\) của hai tam giác BDA' và B'D'C
c) Chứng minh \({G_{1}, {G_{2}}^{}}^{}\) chia đoạn AC' thành ba phần bằng nhau.
d) Gọi O và I lần lượt là tâm của các hình bình hành ABCD và AA'C'C. Xác định thiết diện của mặt phẳng (A'IO) với hình hộp đã cho.
Hướng dẫn giải chi tiết bài 3
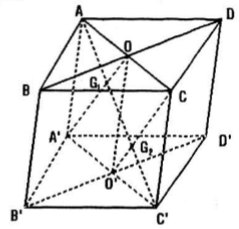
Câu a:
Ta có:
BB'D'D và A'B'CD là các hình bình hành nên:
BD // B'D' và DA' // B'C
⇒ Hai mặt phẳng (BDA') và (B'D'C) có các cặp đường thẳng cắt nhau và song song với nhau từng đôi một.
⇒ (BDA') // (B'D'C)
Câu b:
Gọi O, O' lần lượt là tâm của hình bình hành ABCD và A'B'C'D'.
Trong mặt phẳng (AA'C'C), gọi G1, G2 lần lượt là trọng tâm của AC' với A'O và O'C.
Ta chứng minh G1, G2 lần lượt là trọng tâm của tam giác A'BD và tam giác CB'D'.
Thật vậy ta có: \(\Delta G_1OA\sim G_1A'C'\) (vì AC // A'C')
\(\frac{G_1O}{G_1A'}=\frac{OA}{A'C'}=\frac{1}{2}\Rightarrow \frac{AG_1}{A'O}=\frac{2}{3}\Rightarrow G_1\) là trọng tâm của tam giác A'BD.
Tương tự G2 là trọng tâm của \(\Delta CB'D'.\)
Vậy AC' đi qua G1, G2 là trọng tâm của hai tam giác BDA' và B'D'C.
Câu c:
Theo câu b) ta có:
\(\frac{AG_1}{G_1C'}=\frac{AO}{A'C'}=\frac{1}{2} \ (vi \ \Delta G_1OA\sim \Delta G_1A'C')\)
\(\Rightarrow AG_1=\frac{1}{3}AC' \ (1)\)
Tương tự:
\(\frac{C'G_2}{G_2A}=\frac{C'O'}{CA}=\frac{1}{2}\) (vì \(\Delta G_2C'O' \sim \Delta G_2AC\))
\(\Rightarrow C'G_2=\frac{1}{3}AC'(2)\)
Từ (1) và (2) \(\Rightarrow AG_1=G_1G_2=G_2C'\)
Vậy \(G_1, G_2\) chia đoạn AC' thành 3 phần bằng nhau.
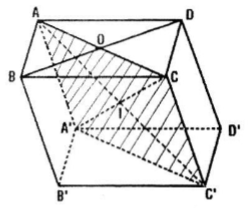
Câu d:
Ta có:
\(O\in AC\Rightarrow O\in (ACC'A')\)
\(I \in (ACC'A')\) và \(A' \in (ACC'A')\)
⇒ Hai mặt phẳng (A'IO) và (ACC'A') trùng nhau.
⇒ Thiết diện của mặt phẳng (A'IO) với hình hộp là hình bình hành ACC'A'.
-- Mod Toán 11 HỌC247
-


Cho hai mặt phẳng song song (α) và (β). Đường thẳng d nằm trong (α) (h.2.47). Hỏi d và (β) có điểm chung không?
bởi Nguyễn Lệ Diễm
 25/02/2021
25/02/2021
.png) Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho hình lăng trụ ABC.A’B’C’. gọi I. J. K lần lượt là trọng tâm của các tam giác ABC, ACC’, A’B’C’. Mặt phẳng nào sau đây song song với (IJK)
bởi Nguyễn Minh Minh
 21/01/2021
21/01/2021
A. (AA’B’)
B. (AA’C’)
C. (A’B’C’)
D. (BB’C’)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 1 trang 71 SGK Hình học 11
Bài tập 2 trang 71 SGK Hình học 11
Bài tập 4 trang 71 SGK Hình học 11
Bài tập 2.22 trang 76 SBT Hình học 11
Bài tập 2.23 trang 76 SBT Hình học 11
Bài tập 2.24 trang 77 SBT Hình học 11
Bài tập 2.25 trang 77 SBT Hình học 11
Bài tập 2.26 trang 77 SBT Hình học 11
Bài tập 2.27 trang 77 SBT Hình học 11
Bài tập 2.28 trang 77 SBT Hình học 11
Bài tập 2.29 trang 77 SBT Hình học 11
Bài tập 2.30 trang 78 SBT Hình học 11
Bài tập 2.31 trang 78 SBT Hình học 11
Bài tập 29 trang 67 SGK Hình học 11 NC
Bài tập 30 trang 67 SGK Hình học 11 NC
Bài tập 31 trang 68 SGK Hình học 11 NC
Bài tập 32 trang 68 SGK Hình học 11 NC
Bài tập 33 trang 68 SGK Hình học 11 NC
Bài tập 34 trang 68 SGK Hình học 11 NC
Bài tập 35 trang 68 SGK Hình học 11 NC
Bài tập 36 trang 68 SGK Hình học 11 NC
Bài tập 37 trang 68 SGK Hình học 11 NC





