Giải bài 1 tr 71 sách GK Toán Hình lớp 11
Trong mặt phẳng \((\alpha )\) cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường thẳng a,b,c,d song song với nhau và không nằm trên \((\alpha )\). Trên a, b, c lần lượt lấy ba điểm A', B', C' tùy ý:
a) Hãy xác định giao điểm D' của đường thẳng d với mặt phẳng (A'B'C').
b) Chứng minh A'B'C'D' là hình bình hành.
Hướng dẫn giải chi tiết bài 1
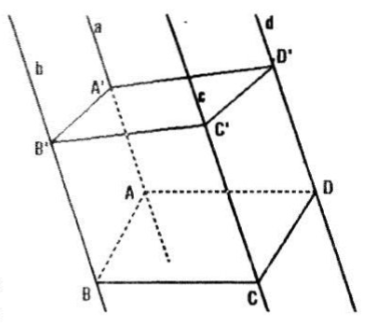
Câu a:
Ta có:
\(\left.\begin{matrix} a // b\\ AD // BC\\ a\cap AD= A \end{matrix}\right\}\Rightarrow (a,d) // (b, c)\)
Tương tự ta có: (a, b) // (c, d).
Vì hai mặt phẳng (a, b) và (c, d) song song với nhau nên mp(A'B'C) cắt 2 mặt phẳng này lần lượt theo 2 giao tuyến A'B' và C'D' song song với nhau.
⇒ D' là giao điểm của đường thẳng qua C' và song song với A'B'.
Câu b:
Theo câu a) ta có:
A'B' // C'D'
Tương tự vì (a, b) // (c, d) ⇒ A'D' // B'C'
Vậy tứ giác A'B'C'D' là hình bình hành.
-- Mod Toán 11 HỌC247
-


Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của AD, BC, SA. Chứng minh (MNP) // (SCD).
bởi Châu Lê Ngọc
 26/11/2021
26/11/2021
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của AD, BC, SA.
- Chứng minh (MNP) // (SCD).
- (MNP) cắt SB tại Q. Chứng minh: Q là trung điểm SB.
- MP và NQ cắt nhau tại I. Chứng minh: SI song song với AD và BC.
Theo dõi (0) 0 Trả lời -


Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60°. Tính độ dài đường cao chủa hình chóp đã cho.
bởi Vũ Thị Thanh Hương
 19/04/2021
Toán hình lớp 11Theo dõi (0) 0 Trả lời
19/04/2021
Toán hình lớp 11Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 2 trang 71 SGK Hình học 11
Bài tập 3 trang 71 SGK Hình học 11
Bài tập 4 trang 71 SGK Hình học 11
Bài tập 2.22 trang 76 SBT Hình học 11
Bài tập 2.23 trang 76 SBT Hình học 11
Bài tập 2.24 trang 77 SBT Hình học 11
Bài tập 2.25 trang 77 SBT Hình học 11
Bài tập 2.26 trang 77 SBT Hình học 11
Bài tập 2.27 trang 77 SBT Hình học 11
Bài tập 2.28 trang 77 SBT Hình học 11
Bài tập 2.29 trang 77 SBT Hình học 11
Bài tập 2.30 trang 78 SBT Hình học 11
Bài tập 2.31 trang 78 SBT Hình học 11
Bài tập 29 trang 67 SGK Hình học 11 NC
Bài tập 30 trang 67 SGK Hình học 11 NC
Bài tập 31 trang 68 SGK Hình học 11 NC
Bài tập 32 trang 68 SGK Hình học 11 NC
Bài tập 33 trang 68 SGK Hình học 11 NC
Bài tập 34 trang 68 SGK Hình học 11 NC
Bài tập 35 trang 68 SGK Hình học 11 NC
Bài tập 36 trang 68 SGK Hình học 11 NC
Bài tập 37 trang 68 SGK Hình học 11 NC





