Giải bài 4 tr 71 sách GK Toán Hình lớp 11
Cho hình chóp S.ABCD. Gọi \({A_{1}}^{}\) là trung điểm của cạnh SA và \({A_{2}}^{}\) là trung điểm của đoạn \(A{A_{1}}^{}\). Gọi \((\alpha )\) và \((\beta )\)là hai mặt phẳng song song với mặt phẳng (ABCD) và lần lượt đi qua \({A_{1}}^{}\), \({A_{2}}^{}\). Mặt phẳng \((\alpha )\) cắt các cạnh SB, SC, SD lần lượt tại \({B_{1}, {C_{1}, {D_{1}}^{}}^{}}^{}\). Mặt phẳng \((\beta )\) cắt các cạnh SB, SC, SD lần lượt tại \({B_{2}, {C_{2},{D_{2}}^{}}^{}}^{}\). Chứng minh:
a) \({B_{1}, {C_{1}, {D_{1}}^{}}^{}}^{}\) lần lượt là trung điểm của các cạnh SB, SC, SD
b) \({B_1}{B_2} = {B_2}B,\,\,{C_1}{C_2} = {C_2}C,\,\,{D_1}{D_2} = {D_2}D\)
c) Chỉ ra các hình chóp cụt có một đáy là tứ giác ABCD.
Hướng dẫn giải chi tiết bài 4
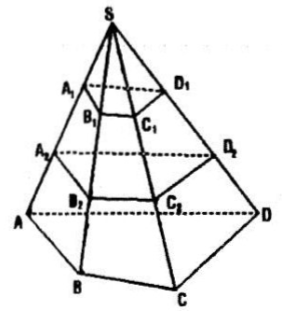
Câu a:
Vì mặt phẳng (SAB) cắt hai mặt phẳng song song \((\alpha )\) và (ABCD) theo hai giao tuyến lần lượt A1B1 và AB.
⇒ A1B1 // AB.
⇒ A1B1 là đường trung bình của tam giác SAB.
⇒ B1 là trung điểm của SB.
Tương tự ta có:
B1C1 là đường trung bình của tam giác SBC.
⇒ C1 là trung bình của SC.
C1D1 là đường trung bình của tam giác SCD.
⇒ D1 là trung điểm của SD.
Câu b:
Vì mp(SAB) cắt hai mặt phẳng song song \((\beta )\) và (ABCD) theo 2 giao tuyến lần lượt là A2B2 và AB.
⇒ A2B2 // AB
⇒ A2B2 là trung bình của hình thang A1B1BA
⇒ B1B2 = B2B
Tương tự: B2C2 là đường trung bình của hình thang B1C1CB
⇒ C1C2 = C2C
C2D2 là đường trung bình của hình thang C1D1DC
⇒ D1D2 = D2D
Câu c:
Có 2 hình chóp cụt có đáy là tứ giác ABCD đó là: A1B1C1D1.ABCD và A2B2C2D2.ABCD.
-- Mod Toán 11 HỌC247
-


Cho hình bình hành ABCD. Gọi Bx, Cy, Dz là các đường thẳng đi qua B, C, D và song song với nhau. Mặt phẳng (∝) đi qua A và cắt Bx, Cy, Dz lần lượt tại A’, C’, D’ với BB’ = 2, DD’ = 4. Khi đó CC’ bằng:
bởi Nguyen Ngoc
 22/01/2021
22/01/2021
A. 3
B. 4
C. 5
D. 6
Theo dõi (0) 1 Trả lời -


Cho tứ diện đều S.ABC. Gọi I là trung điểm của AB, M là một điểm lưu động trên đoạn AI. Qua M vẽ mặt phẳng (∝) //(SIC). Khi đó thiết diện của mặt phẳng (∝) và tứ diện S.ABC là:
bởi My Van
 21/01/2021
21/01/2021
A. tam giác cân tại M
B. tam giác đều
C. hình bình hành
D. hình thoi
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 2 trang 71 SGK Hình học 11
Bài tập 3 trang 71 SGK Hình học 11
Bài tập 2.22 trang 76 SBT Hình học 11
Bài tập 2.23 trang 76 SBT Hình học 11
Bài tập 2.24 trang 77 SBT Hình học 11
Bài tập 2.25 trang 77 SBT Hình học 11
Bài tập 2.26 trang 77 SBT Hình học 11
Bài tập 2.27 trang 77 SBT Hình học 11
Bài tập 2.28 trang 77 SBT Hình học 11
Bài tập 2.29 trang 77 SBT Hình học 11
Bài tập 2.30 trang 78 SBT Hình học 11
Bài tập 2.31 trang 78 SBT Hình học 11
Bài tập 29 trang 67 SGK Hình học 11 NC
Bài tập 30 trang 67 SGK Hình học 11 NC
Bài tập 31 trang 68 SGK Hình học 11 NC
Bài tập 32 trang 68 SGK Hình học 11 NC
Bài tập 33 trang 68 SGK Hình học 11 NC
Bài tập 34 trang 68 SGK Hình học 11 NC
Bài tập 35 trang 68 SGK Hình học 11 NC
Bài tập 36 trang 68 SGK Hình học 11 NC
Bài tập 37 trang 68 SGK Hình học 11 NC





