Giải bài 2.47 tr 85 SBT Toán 11
Một tổ có 7 nam và 3 nữ. Chọn ngẫu nhiên hai người. Tìm xác suất sao cho trong hai người đó:
a) Cả hai đều là nữ;
b) Không có nữ nào;
c) Ít nhất một người là nữ;
d) Có đúng một người là nữ.
Hướng dẫn giải chi tiết
a) Chọn ngẫu nhiên 2 người của một tổ 10 người nên số phần tử của không gian mẫu là \(n({\rm{\Omega }}) = C_{10}^2\).
Kí hiệu A2 là biến cố: "Hai người đã chọn đều là nữ".
Biến cố A2 là chọn 2 người nữ trong 3 người nữ nên số phần tử của biến cố là \(n({A_2}) = C_3^2\)
Vậy xác suất sao cho hai người được chọn đều là nữ là \(P\left( {{A_2}} \right) = \frac{{n\left( {{A_2}} \right)}}{{n\left( {\rm{\Omega }} \right)}} = \frac{{C_3^2}}{{C_{10}^2}} = \frac{3}{{45}} = \frac{1}{{15}}\).
b) Kí hiệu A0 là biến cố: "Trong hai người đã chọn không có nữ nào".
Biến cố A0 là chọn 2 người nam trong 7 người nam.
Khi đó số phần tử của biến cố \(n({A_0}) = C_7^2\)
Vậy xác suất sao cho trong hai người được chọn không có nữ là \(P({A_0}) = \frac{{n({A_0})}}{{n(\Omega )}} = \frac{{C_7^2}}{{C_{20}^2}} = \frac{{21}}{{45}} = \frac{7}{{15}}\)
c) Biến cố trong 2 người được chọn có ít nhất một người là nữ là biến cố đối của biến cố A0 không có người nữ nào.
Do đó theo hệ quả với mọi biến cố A ta có \(P\left( {\bar A} \right) = 1 - P(A)\)
Ta có \(P\left( {\overline {{A_0}} } \right) = 1 - P\left( {{A_0}} \right) = 1 - \frac{7}{{15}} = \frac{8}{{15}}\)
d) Kí hiệu A1 là biến cố: "Trong hai người có một nữ".
Biến cố A1 là chọn 1 nữ trong 3 nữ và chọn 1 bạn nam trong 7 bạn nam.
Nên số phần tử của biến cố là: \(n({A_1}) = C_7^1.C_3^1\)
Vậy xác suất sao cho trong hai người được chọn có một nữ là
\(P\left( {{A_1}} \right) = \frac{{n({A_1})}}{{n({\rm{\Omega }})}} = \frac{{C_7^1C_3^1}}{{C_{10}^2}} = \frac{{21}}{{45}} = \frac{7}{{15}}\)
-- Mod Toán 11 HỌC247
-

 Tính số cách sắp xếpTheo dõi (0) 4 Trả lời
Tính số cách sắp xếpTheo dõi (0) 4 Trả lời -


Tính xác suất để số chấm xuất hiện ở hai lần gieo có đúng một lần là bội của 2
bởi dương VĂN TUẤN
 02/01/2020
02/01/2020
Gieo một con súc sắc cân đối và đồng chất 2 lần lien tiếp.
- Tính xác suất để số chấm xuất hiện ở hai lần gieo có đúng một lần là bội của 2.
Theo dõi (0) 2 Trả lời -


Tính xác suất để trong số đó luôn xuất hiện 3 chữ số 2, các chữ số còn lại đôi một khác nhau
bởi Anh lê
 01/01/2020
01/01/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính xác suất để chọn được 2 số có tích là một số lẻ
bởi Anh lê
 01/01/2020
01/01/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tính xác xuất 3 quả lấy ra đủ 3 màu biết hộp có 12 quả cầu gồm 3 quả cầu xanh 4 quả cầu đỏ 5 cầu vàng
bởi Dương Hoa
 27/12/2019
Giải bài toán giúp em ạTheo dõi (0) 4 Trả lời
27/12/2019
Giải bài toán giúp em ạTheo dõi (0) 4 Trả lời -


Tìm xác suất để trong 3 bi lấy ra sau có 2 bi trắng biết hộp 1 đựng 8 bi trắng và 2 bi đen, hộp 2 đựng 9 bi trắng và 1 bi đen
bởi Trần Hoàng Thiên
 26/12/2019
Có 2 hộp, hộp 1 đựng 8 bi trắng và 2 bi đen; hộp 2 đựng 9 bi trắng và 1 bi đen. Lấy ngẫu nhiên 2 viên bi từ hộp 1 bỏ sang hộp 2 rồi sau đó lấy ngẫu nhiên 3 bi từ hộp 2. Tìm xác suất để trong 3 bi lấy ra sau có 2 bi trắng.Theo dõi (0) 1 Trả lời
26/12/2019
Có 2 hộp, hộp 1 đựng 8 bi trắng và 2 bi đen; hộp 2 đựng 9 bi trắng và 1 bi đen. Lấy ngẫu nhiên 2 viên bi từ hộp 1 bỏ sang hộp 2 rồi sau đó lấy ngẫu nhiên 3 bi từ hộp 2. Tìm xác suất để trong 3 bi lấy ra sau có 2 bi trắng.Theo dõi (0) 1 Trả lời -


Tìm xác xuất để số đó chọn có tổng cấc chữ số bằng 10
bởi 姮阮
 26/12/2019
Cho tập hớp a12345 gọi s la tập hớp tất cách các số tự nhiên có ít nhất 3 chữ số các chữ số đôi 1 khác nhau đc thành lập từ các chữ số thuộc tập A chon ngâu nhiên 1 số từ s tim xác xuất p để số đó chọn có tổng các shuwx số bằng 10Theo dõi (0) 0 Trả lời
26/12/2019
Cho tập hớp a12345 gọi s la tập hớp tất cách các số tự nhiên có ít nhất 3 chữ số các chữ số đôi 1 khác nhau đc thành lập từ các chữ số thuộc tập A chon ngâu nhiên 1 số từ s tim xác xuất p để số đó chọn có tổng các shuwx số bằng 10Theo dõi (0) 0 Trả lời -

 Ôn tập
Ôn tập Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Ném ngẫu nhiên 1 đồng xu 3 lần, xác suất để có đúng 2 lần xuất hiện mặt ngửa là?
bởi Trần Trân
 23/12/2019
Ném ngẫu nhiên 1 đồng xu 3 lần. Xác suất để có đúng 2 lần xuất hiện mặt ngửa là ?Theo dõi (0) 1 Trả lời
23/12/2019
Ném ngẫu nhiên 1 đồng xu 3 lần. Xác suất để có đúng 2 lần xuất hiện mặt ngửa là ?Theo dõi (0) 1 Trả lời -


Chọn ngẫu nhiên một số nguyên dương không quá 20, xác suất để số được chọn là số nguyên tố là ?
bởi Trần Trân
 23/12/2019
Chọn ngẫu nhiên một số nguyên dương không quá 20. Xác suất để số được chọn là số nguyên tố là ?Theo dõi (0) 1 Trả lời
23/12/2019
Chọn ngẫu nhiên một số nguyên dương không quá 20. Xác suất để số được chọn là số nguyên tố là ?Theo dõi (0) 1 Trả lời -


Tính xác xuất để chọn được số luôn có mặt số 0 và số 1 đồng thời hai số này không đứng cạnh nhau
bởi Nguyễn Phương Lan
 22/12/2019
22/12/2019
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính xác suất lấy được 3 thẻ có tích các số ghi trên thẻ là một số chia hết cho 3
bởi Lậpp Trung
 20/12/2019
20/12/2019
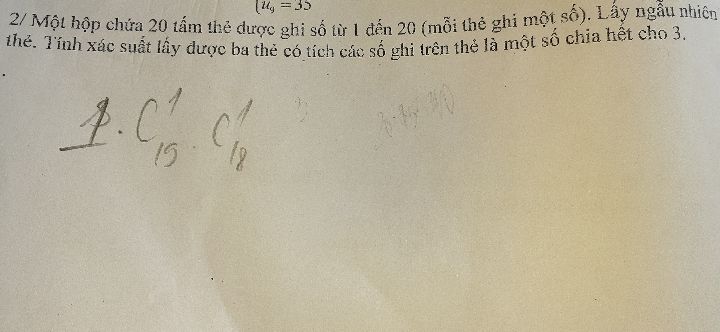 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 6 trang 74 SGK Đại số & Giải tích 11
Bài tập 7 trang 75 SGK Đại số & Giải tích 11
Bài tập 2.48 trang 85 SBT Toán 11
Bài tập 2.49 trang 85 SBT Toán 11
Bài tập 2.50 trang 85 SBT Toán 11
Bài tập 2.51 trang 85 SBT Toán 11
Bài tập 2.52 trang 86 SBT Toán 11
Bài tập 2.53 trang 86 SBT Toán 11
Bài tập 2.54 trang 86 SBT Toán 11
Bài tập 2.55 trang 86 SBT Toán 11
Bài tập 2.56 trang 86 SBT Toán 11
Bài tập 25 trang 75 SGK Toán 11 NC
Bài tập 26 trang 75 SGK Toán 11 NC
Bài tập 27 trang 75 SGK Toán 11 NC
Bài tập 28 trang 76 SGK Toán 11 NC
Bài tập 29 trang 76 SGK Toán 11 NC
Bài tập 30 trang 76 SGK Toán 11 NC
Bài tập 31 trang 76 SGK Toán 11 NC
Bài tập 32 trang 76 SGK Toán 11 NC
Bài tập 33 trang 76 SGK Toán 11 NC
Bài tập 34 trang 83 SGK Toán 11 NC
Bài tập 35 trang 83 SGK Toán 11
Bài tập 36 trang 83 SGK Toán 11 NC
Bài tập 37 trang 83 SGK Toán 11 NC
Bài tập 38 trang 85 SGK Toán 11 NC
Bài tập 39 trang 85 SGK Toán 11 NC
Bài tập 40 trang 85 SGK Toán 11 NC





