Cho hình chóp tứ giác đều S.ABCD. Gọi A', B', C', D' theo thứ tự là trung điểm của AB, BC, CD, DA.

Ta thấy 2 hình chóp S.ABCD và S.A'B'C'D'. Có chung chiều cao kẻ từ đỉnh S xuống đáy. Vậy để đi tìm tỉ số khoảng cách thì chúng ta chỉ cần tìm tỉ số diện tích 2 đáy mà ta có hình vẽ như sau:

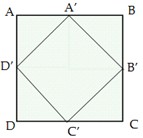
Ta thấy:

\({S_{A'B'C'D'}} = A'D'.A'B' = {\left( {\frac{{a\sqrt 2 }}{2}} \right)^2} = \frac{{{a^2}}}{2} = \frac{1}{2}{S_{ABCD}}\)

\(\Rightarrow \frac{{{V_{A'B'C'D'}}}}{{{V_{ABCD}}}} = \frac{1}{2}\) => Đáp án A.