Phương pháp giải bài toán liên quan đến chiều dài của lò xo và thời gian lò xo nén, dãn

1.1. Bài toán liên quan đến chiều dài của lò xo

Xét trường hợp vật ở dưới.

+ Tại VTCB: \({{\ell }_{CB}}={{\ell }_{0}}+\Delta {{\ell }_{0}}\)

+ Tại vị trí li độ x: 

\(\ell = {\ell _{CB}} + x\left\{ \begin{array}{l} {\ell _{\max }} = {\ell _{CB}} + A\\ {\ell _{\min }} = {\ell _{CB}} - A \end{array} \right.\)

+ Nếu \(A\le \Delta \ell \) thì khi dao động lò xo luôn luôn bị dãn:

+ Dãn ít nhất (khi vật cao nhất): \(\Delta {{\ell }_{0}}-A\)

+ Dãn nhiều nhất (khi vật thấp nhất): \(\Delta {{\ell }_{0}}+A\)

+ Nếu A > Δl thì khi dao động lò xo có lúc dãn có lúc nén:

+ Nén nhiều nhất (khi vật cao nhất): \(A-\Delta {{\ell }_{0}}\)

+ Không hiến dạng khi: \(x=-\Delta {{\ell }_{0}}\)

+ Dãn nhiều nhất (khi vật thấp nhất): \(\Delta {{\ell }_{0}}+A.\)

1.2. Bài toán liên quan đến thòi gian lò xo nén dãn

Nếu \(A\le \Delta {{\ell }_{0}}\) thì trong quá trình dao động lò xo luôn luôn dãn. Vì vậy ta xét các trường hợp \(A\ge \Delta {{\ell }_{0}}!\)

Trong một chu kỳ thời gian lò xo nén, thời gian lò xo dãn lần lượt là:

\(\left\{ \begin{array}{l} {t_{nen}} = 2.\frac{1}{\omega }\arccos \frac{{\Delta {\ell _0}}}{A} = \frac{T}{\pi }\arccos \frac{{\Delta {\ell _0}}}{A}\\ {t_{dan}} = T - 2.\frac{1}{\omega }\frac{{\Delta {\ell _0}}}{A} = T - \frac{T}{\pi }\arccos \frac{{\Delta {\ell _0}}}{A} \end{array} \right.\)

Kinh nghiệm: Trong các đề thi hiện hành phổ biến là trường hợp Δl₀ = A/2 Lúc này, trong 1 chu là thời gian lò xo nén là T/3 và thời gian lò xo dãn là 2T/3.

Ví dụ 1:  Một lò xo khối lượng không đáng kể có độ cứng k, một đầu gắn vật nhỏ có khối lượng m, đầu còn lại được gắn vào một điểm cố định J sao cho vật dao động điều hòa theo phương ngang. Trong quá trình dao động, chiều dài cực đại và chiều dài cực tiểu của lò xo lần lượt là 40 cm và 30 cm. Chọn phương án sai.

A. Chiều dài tự nhiên của lò xo là 35 cm.

B. Biên độ dao động là 5 cm.

C. Lực mà lò xo tác dụng lên điểm J luôn là lực kéo.

D. Độ biến dạng của lò xo luôn bằng độ lớn của li độ.

Hướng dẫn

Vì khi ở vị trí cân bằng lò xo không biến dạng nên độ biến dạng của lò xo luôn bằng độ lớn của li độ => D đúng.

Chiều dài cực đại và cực tiểu của lò xo lần lượt là:

\(\left\{ \begin{array}{l} {\ell _{\max }} = {\ell _{CB}} + A = {\ell _0} + A\\ {\ell _{\min }} = {\ell _{CB}} - A = {\ell _0} - A \end{array} \right. \Rightarrow \left\{ \begin{array}{l} {\ell _0} = \frac{{{\ell _{\max }} + {\ell _{\min }}}}{2} = 35\left( {cm} \right)\\ A = \frac{{{\ell _{\max }} - {\ell _{\min }}}}{2} = 5\left( {cm} \right) \end{array} \right. \Rightarrow A,B\) đúng

Trong một chu kì một nửa thời gian lò xo nén (lực lò xo tác dụng lên J là lực đẩy) và một nửa thời gian lò xo dãn (lực lò xo tác dụng lên J là lực kéo) → C sai → Chọn C.

Ví dụ 2:  Con lắc lò xo đang dao động điều hòa theo phương ngang với biên độ \(A=4\sqrt{2}\) (cm). Biết lò xo có độ cứng k = 50 (N/m), vật dao động có khối lượng m = 200 (g), lấy π²= 10. Khoảng thời gian trong một chu kỳ để lò xo dãn một lượng lớn hơn \(2\sqrt{2}\)  cm là

A. 2/15 (s).                 

B. 1/15 (s).     

C. 1/3 (s).                   

D. 0,1 (s)

Hướng dẫn

Để lò xo dãn lớn hơn \(2\sqrt{2}\)cm = A/2 thì vật có li độ nằm trong khoảng x = A/2 đến A:

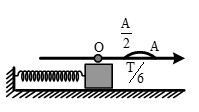
\(\Delta t=\frac{T}{6}+\frac{T}{6}=\frac{T}{3}\)

\(=\frac{1}{3}2\pi \sqrt{\frac{m}{k}}=\frac{1}{3}2\pi \sqrt{\frac{0,2}{50}}=\frac{2}{15}\left( s \right)\Rightarrow \) Chọn A.

Ví dụ 3: Một lò xo nhẹ có chiều dài tự nhiên 30 cm có độ cứng là k, đầu trên cố định, đầu dưới gắn vật m, vật dao động điều hoà trên mặt phẳng nghiêng góc 30° với phương trình x = 6cos(10t + 5π/6) (cm) (t đo bằng s) tại nơi có g = 10 (m/s²). Trong quá trình dao động chiều dài cực tiểu của lò xo là

A. 29 cm.                   

B. 25 cm.                    

C. 31 cm.                   

D. 36 cm.

Hướng dẫn

Độ dãn của lò xo thẳng đứng khi vật ở VTCB:

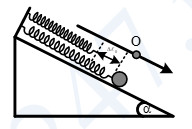
\(\Delta {{\ell }_{0}}=\frac{mg\sin \alpha }{{{\omega }^{2}}}=\frac{g\sin \alpha }{{{\omega }^{2}}}=0,05\left( m \right)\)

Chiều dài lò xo tại VTCB (\({{\ell }_{0}}\) là chiều dài tự nhiên) \({{\ell }_{CB}}={{\ell }_{0}}+\Delta {{\ell }_{0}}=35\left( cm \right)\)

Chiều dài cực tiểu (khi vật ở vị trí cao nhất): \({{\ell }_{\min }}={{\ell }_{cb}}-A=29\left( cm \right)\Rightarrow \) Chọn A.

Chú ý: Khi lò xo có độ dãn Δl thì độ lớn li độ là: \(\left| {{x}_{0}} \right|=\left| \Delta \ell -\Delta {{\ell }_{0}} \right|\)

Ví dụ 4:  Con lắc lò xo treo thẳng đứng, gồm lò xo độ cứng 100 (N/m) và vật nặng khối lượng 100 (g). Giữ vật theo phưong thẳng đứng làm lò xo dãn 3 (cm), rồi truyền cho nó vận tốc \(20\pi \sqrt{3}\)  (cm/s) hướng lên thì vật dao động điều hòa Lấy π² = 10; gia tốc trọng trường g = 10 (m/s²). Biên độ dao động là

A. 5,46 (cm).              

B. 4,00 (cm).              

C. 4,58 (cm).              

D. 2,54 (cm).

Hướng dẫn

\(\omega = \sqrt {\frac{k}{m}} = 10\pi \left( {rad/s} \right);\Delta {\ell _0} = \frac{{mg}}{k} = 1\left( {cm} \right);\left\{ \begin{array}{l} \left| {{x_{\left( 0 \right)}}} \right| = \left| {\Delta \ell - \Delta {\ell _0}} \right| = 2\left( {cm} \right)\\ \left| {{v_{\left( 0 \right)}}} \right| = 20\pi \sqrt 3 \left( {cm/s} \right) \end{array} \right.\)

\(\Rightarrow A=\sqrt{x_{0}^{2}+\frac{v_{0}^{2}}{{{\omega }^{2}}}}=4\left( cm \right)\Rightarrow \) Chọn B

Bài 1: Con lắc lò xo treo thẳng đứng, gồm lò xo độ cứng 40 (N/m) và vật nặng khối lượng 100 (g). Lấy π² = 10; gia tốc trọng trường g = 10 (m/s²). Giữ vật theo phương thẳng đứng làm lò xo dãn 3,5 (cm), rồi truyền cho nó vận tốc 20 (cm/s) hướng lên thì vật dao động điều hòa Biên độ dao động là

A. 2 (cm).                   

B. 3,6 cm.                   

C. \(2\sqrt{2}\) cm.               

D. \(\sqrt{2}\) cm.

Bài 2: Con lắc lò xo treo thẳng đứng, gồm lò xo độ cứng 62,5 (N/m) và vật nặng khối lượng 100 (g). Giữ vật theo phương thẳng đứng làm lò xo dãn 3,2 (cm), rồi tmyền cho nó vận tốc 60 (cm/s) hướng lên thì vật dao động điều hòa Lấy π² = 10; gia tốc trọng trường g = 10 (m/s²). Biên độ dao động là

A. 5,46 (cm).              

B. 4,00 (cm).              

C. \(0,8\sqrt{13}\)  (cm).       

D. 2,54(cm)

Bài 3: Con lắc lò xo treo thẳng đứng. Nâng vật lên đến vị trí lò xo không biến dạng và thả không vận tốc ban đầu thì vật dao động điều hòa theo phương thẳng đứng trùng với trục của lò xo, khi vận tốc của vật là 1 m/s thì gia tốc của vật là 5 m/s². Lấy gia tốc trọng trường 10 m/s². Tần số góc có giá trị là:

A. 2rad/s.                   

B. 3 rad/s.                   

C. 4rad/s.                   

D. \(5\sqrt{3}\) rad/s

Bài 4: Con lắc lò xo treo thẳng đứng. Nâng vật lên đến vị trí lò xo không biến dạng và thả không vận tốc ban đầu thì vật dao động điều hòa theo phương thẳng đứng trùng với trục của lò xo, khi vận tốc của vật là \(\sqrt{3}\) m/s thì gia tốc của vật là 5 m/s². Lấy gia tốc trọng trường 10 m/s². Tần số góc có giá trị là:

A. 5rad/s.                   

B. 3 rad/s.                   

C. 4rad/s.                   

D. 5\(\sqrt{3}\)rad/s

Bài 5: Một con lắc lò xo dao động điều hòa theo thẳng đứng (trùng với trục của lò xo), khi vật ở cách vị trí cân bằng 4 cm thì có tốc độ bằng không và lò xo không biến dạng. Cho gia tốc trọng trường 9,8 m/s². Tốc độ của vật khi đi qua vị trí cân bằng là

A. 0,626 m/s.              

B. 6,26 cm/s.              

C. 6,26 m/s.                

D. 0,633 m/s.

Bài 6: Một con lắc lò xo dao động điều hòa theo phương thẳng đứng với tần số góc ω tại vị trí có gia tốc trọng trường g. Khi qua vị trí cân bằng lò xo dãn:

A. ω/g.           

B. ω²/g.           

C. g/ω².         

D. g/ω.

Bài 7: Một lò xo có độ cứng k treo thẳng đứng, đầu trên cố định, đầu dưới gắn vật. Cho con lắc dao động điều hòa theo phương thẳng đứng với tần số góc 14 (rad/s) tại nơi có gia tốc trọng trường g = 9,8 (m/s²). Độ dãn cảu lò xo khi vật ở vị trí cân bằng là:

A. 1 cm.                    

B. 5 cm.      

C. 10 cm.                   

D. 2,5 cm.

Bài 8: Một vật nặng gắn vào lò xo và đặt trên mặt phẳng nghiêng 30° so với mặt phẳng ngang thì lò xo dãn ra một đoạn 0,4 (cm). Lấy gia tốc trọng trường g = 10 m/s². Hãy tính chu kỳ dao động của con lắc.

A 0,178 (s).                

B. 1,78 (s).                 

C. 0,562 (s).               

D. 222 (s).

Bài 9: Một con lắc lò xo có độ cứng là k treo trên mặt phăng nghiêng, đầu trên cố định, đầu dưới gắn vật có khối lượng m. Độ dãn của lò xo khi vật ở vị trí cân bằng là 4,9\)\sqrt{2}\) (cm). Cho con lắc dao động điều hòa theo mặt phẳng nghiêng theo phương trình x = 6.cos(10t + 5π /6) (cm) (t đo bằng giây) tại nơi có gia tốc trọng trường g = 9,8 (m/s²). Góc giữa mặt phẳng nghiêng và mặt phẳng ngang là

A. 30°.            

B. 45 .                        

C. 60°.         

D. 15°.

Bài 10: Một con lắc lò xo dao động điều hòa theo phương thẳng đứng. Chiều dài tự nhiên của lò xo là 30 cm, còn trong khi dao dộng chiều dài biến thiên từ 32 cm đến 38 cm. Lấy gia tốc trọng trường g = 10 m/s². Vận tốc cực đại của vật nặng là:         

A. 60 \(\sqrt{2}\)cm/s.           

B. 30 \(\sqrt{2}\)cm/s.           

C.  30 cm/s                 

D. 60 cm/s

Bài 11: Con lắc lò xo treo thẳng đứng, ở vị trí cân bằng lò xo dãn 2 cm. Khi lò xo có chiều dài cực tiểu thì nó bị nén 4 cm. Khi lò xo có chiều dài cực đại thì nó

A. dãn 4 cm.               

B. dãn 8 cm.               

C. dãn 2 cm.               

D. nén 2 cm.

Bài 12: Một lò xo treo thẳng đứng, đầu trên cố định, đầu dưới gắn vật. Cho con lắc dạo động điều hòa theo phương thẳng đứng với tần số góc 20 (rad/s), tại nơi có gia tốc trọng trường g = 10 (m/s²), ở một thời điểm nào đó vận tốc vật dao động triệt tiêu thì lò xo bị nén 1,5 cm. Khi lò xo dãn 6,5 cm thì tốc độ dao động của vật là

A. 1 m/s.                     

B. 0 cm/s.                   

C. 10 cm/s.                 

D. 2,5 cm/s.

Bài 13: Một con lắc lò xo treo thẳng đứng, vật treo có khối lượng m. Kéo vật xuống dưới vị trí cân bằng 3 cm rồi truyền cho nó vận tốc 40 cm/s thì nó dao động điều hòa theo phương thẳng đứng trùng với trục của lò xo và khi vật treo đạt độ cao cực đại, lò xo dãn 5 cm. Lấy gia tốc trọng trường g = 10 m/s². Biên độ dao động là

A. 5 cm.                     

B. 1,15 m.                  

C. 17 cm.                   

D. 2,5 cm.

Bài 14: Một con lắc lò xo treo thẳng đứng, vật treo có khối lượng m. Kéo vật xuống dưới vị trí cân bằng 1,5\(\sqrt{2}\)cm rồi truyền cho nó vận tốc 30 cm/s thì nó dao động điều hòa theo phương thẳng đứng trùng với trục của lò xo và khi vật treo đạt độ cao cực tiểu, lò xo dãn 8 cm. Lấy gia tốc trọng trường g = 10 m/s². Vận tốc cực đại của vật là

A. 0,3\(\sqrt{2}\)m/s.             

B. 1,15 m/s.                

C. 10\(\sqrt{2}\) cm/s.       

D. 25\(\sqrt{2}\)cm/s.

Bài 15: Một con lắc lò xo treo thẳng đứng (coi gia tốc trọng trường 10 m/s²) quả cầu có khối lượng 100 g. Chiều dài tự nhiên của lò xo là 20 cm và chiều dài khi ở vị trí cân bằng là 22,5 cm. Từ vị trí cân bằng, kéo vật thẳng đứng, xuống dưới tới khi lò xo dài 26,5 cm rồi buông nhẹ cho nó dao động điều hòa Động năng của quả cầu khi nó cách vị trí cân bằng 2 cm là

A. 24 mJ.                    

B. 22 mJ.                    

C. 12 mJ.                    

D. 16,5 mJ.

Bài 16: Một lò xo đặt trên mặt phăng nghiêng (nghiêng so với mặt phăng ngang một góc 30°), đầu dưới cố định, đầu trên gắn vật, sao cho vật dao động điều hòa theo phương song song với mặt phẳng nghiêng và trùng với trục của lò xo với tần số góc 10 (rad/s), với biên độ 3 cm. Lấy gia tốc trọng trường 10 (m/s²). Độ nén cực đại của lò xo khi vật dao động là

A. 3 (cm).                   

B. 10 (cm).                 

C. 7 (cm).                   

D. 8 (cm). 

Bài 17: Một con lắc lò xo gồm vật nhỏ khối lượng M và lò xo nhẹ có độ cứng k. Vật dao động điều hòa trên giá đỡ cố định dọc theo trục lò xo và đặt nghiêng so với mặt phẳng ngang một góc 30°. Biên độ dao động 10 cm và lực đàn hồi của lò xo đạt cực đại khi lò nén 15 cm. Tần số góc dao dộng là

A. \(10\sqrt{30}\)rad/s.         

B. \(20\sqrt{6}\) rad/s.                       

C. 10rad/s.                 

D. 10 \(\sqrt{3}\)rad/s.

Bài 18: Chọn phương án sai. Một con lắc lò xo có độ cứng là k treo thẳng đứng, đầu trên cố định, đầu dưới gắn vật. Gọi độ dãn của lò xo khi vật ở vị trí cân bằng là Al₀. Cho con lắc dao động điều hòa theo phương thẳng đứng với biên độ là A (A > Δl₀). Trong quá trình dao động, lò xo

A. bị nén cực đại một lượng là A − Δl₀.

B. bị dãn cực đại một lượng là A + Δl₀

C. không biến dạng khi vật ở vị trí cân bằng.

D. cố lúc bị nén có lúc bị dãn có lúc không biến dạng.

Bài 19: Chọn phương án sai. Một con lắc lò xo có độ cứng là k treo thẳng đứng, đầu trên cố định, đầu dưới gắn vật. Gọi độ dãn của lò xo khi vật ở vị trí cân bằng là Δl₀. Cho con lắc dao động điều hòa theo phương thẳng đúng với biên độ là A (A < Δl₀). Trong quá trình dao động, lò xo

A. bị dãn cực tiểu một lượng là Δl₀ − A.

B. bị dãn cực đại một lượng là A + Δl₀.

C. lực tác dụng của lò xo lên giá treo là lực kéo.

D. có lúc bị nén có lúc bị dãn có lúc không biến dạng.                                

Bài 20: Chọn phương án sai. Một lò xo có độ cúng là k treo trên mặt phẳng nghiêng, đầu trên cố định, đầu dưới gắn vật có khối lượng m. Gọi độ dãn của lò xo khi vật ở vị trí cân bằng là \(\Delta \ell \) . Cho con lắc dao động điều hòa theo mặt phẳng nghiêng với biên độ là A tại nơi có gia tốc trọng trường g.

A. Lực đàn hồi của lò xo có độ lớn nhỏ nhất trong quá trình dao động bằng 0 nêu A >\(\Delta \ell \).

B. Lực đàn hồi của lò xo có độ lớn nhỏ nhất trong quá trình dao động bằng k(Δl − A) nếu A < \(\Delta \ell \).

C. Lực đàn hồi của lò xo có độ lớn lớn nhất trong quá hình dao động bằng k(Δl + A).

D. Góc giữa mặt phẳng nghiêng và mặt phẳng ngang a tính theo công thức mg = k\(\Delta \ell .\sin \alpha .\) .

Bài 21: Một lò xo nhẹ có đầu trên cố định, đầu dưới treo một vật nặng. Tại vị trí cân bằng, lò xo dãn 4 cm. Lấy g = 9,8 m/s². Kéo vật (theo phương thẳng đứng) xuống dưới vị trí cân bằng 2 cm rồi buông nhẹ. Độ lớn gia tốc của vật lúc vừa được buông ra là

A. 4,90 m/s².              

B. 49,0 m/s².              

C. 4,90 cm/s².

D. 49,0 cm/s². 

Bài 22: Một con lắc lò xo dao động điều hòa theo phương thẳng đứng, trung bình cứ mỗi phút vật thực hiện 240 dao động toàn phần. Trong quá trình dao động, lò xo có chiều dài nhỏ nhất là 50cm, chiều dài lớn nhất là 60cm. Chọn gốc tọa độ ở vị trí cân bằng, chiều dương của trục tọa độ hướng xuống dưới, gốc thời gian là lúc lò xo có chiều dài nhỏ nhất. Phương trình vận tốc của vật?

A. v = 40πcos(8πt) (cm/s).                 

B. v = 40πsin(8πt + π) (cm/s),

C. v = 40πsin(8πt) (cm/s).                  

D. v = 80πsin(8πt) (cm/s).

Bài 23: Con lắc lò xo thẳng đứng gồm vật có khối lượng m = 200 g treo vào lò xo độ cứng 100 N/m. Cho vật dao động theo phương thăng đứng với biên độ A = 4 cm. Lấy g = 10 m/s². Độ biến dạng cực đại của lò xo trong quá hình dao động là

A. 4 cm.                     

B. 6 cm.             

C. 8 cm,         

D. 2 cm.

Bài 24: Một con lắc lò xo có tần số riêng là 20 rad/s, được thả rơi tự do mà trục lò xo thẳng đứng, vật nặng bên dưới. Ngay khi con lắc có vận tốc 50\(\sqrt{3}\)cm/s thì đầu trên lò xo bị giữ lại. Cho g = 10 m/s². Biên độ của con lắc lò xo khi dao động điều hòa là

A. 5 cm.                     

B. 6 cm.          

C. 2,5 cm.             

D. 4,5 cm.

Bài 25: Một quả nặng có khối lượng m = 1 kg, nằm trên mặt phẳng nằm ngang, được gắn với lò xo nhẹ có độ cứng k = 100 N/m, theo phương thẳng đứng. Đầu tự do của lò xo bắt đầu được nâng lên thẳng đứng với vận tốc v = 1 m/s. Lấy g = 10 m/s². Xác định độ biến dạng cực đại của lò xo.

A. 1/3 s.                      

B. 0,2 s.            

C. 0,1 s.                 

D. 0,3 s.

Bài 26: Một con lắc lò xo có tần số góc riêng ω = 25 rad/s, rơi tự do mà trục lò xo thẳng đứng, vật nặng bên dưới. Ngay khi con lắc có vận tốc 42 cm/s thì đầu trên lò xo bị giữ lại. Tính vận tốc cực đại của con lắc.

A. 60 cm/s.                 

B. 58 cm/s.                 

C. 73 cm/s.                 

D. 67 cm/s.

ĐÁP ÁN PHẦN LUYỆN TẬP

1.D	2.C	3.D	4.A	5.A	6.C	7.B	8.A	9.B	10.B
11.B	12.B	13.A	14.A	15.A	16.D	17.C	18.C	19.D	20.D
21.A	22.C	23.B	24.A	25.D	26.B

Trên đây là một đoạn trích dẫn nội dung Phương pháp giải bài toán liên quan đến chiều dài của lò xo và thời gian lò xo nén, dãn. Để xem thêm nhiều tài liệu tham khảo hữu ích khác của các chức năng chọn xem trực tuyến hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.

Hy vọng tài liệu này sẽ giúp các em học tập tốt và đạt được thành tích cao trong học tập.