Để giúp các em học sinh có thêm tài liệu học tập, rèn luyện chuẩn bị cho các kì thi sắp tới, HOC247 đã biên soạn, tổng hợp nội dung tài liệu Phương pháp giải bài toán liên quan đến cắt ghép lò xo môn Vật Lý 12 năm 2021-2022 các em học tập rèn luyện tốt hơn. Mời các em tham khảo học tập.
1. PHƯƠNG PHÁP GIẢI
Ta xét các bài toán:
+ Cắt lò xo.
+ Ghép lò xo.
1.1. Cắt lò xo
Giả sử lò xo có cấu tạo đồng đều, chiều dài tự nhiên \({{\ell }_{0}}\) , độ cứng k0, được cắt thành các lò xo khác nhau.
\(k = E\frac{S}{\ell } \Rightarrow k\ell = ES = const{\mkern 1mu} \left\{ \begin{array}{l} {k_0}{\ell _0} = {k_1}{\ell _1} = {k_2}{\ell _2} = .... = {k_n}{\ell _n}\\ {\ell _0} = {\ell _1} + {\ell _2} + ... + {\ell _n} \end{array} \right.\)
Nếu cắt thành 2 lò xo thì
\({k_0}{\ell _0} = k\ell = k'\ell ' \Rightarrow \left\{ \begin{array}{l} k = {k_0}\frac{{{\ell _0}}}{\ell }\\ k' = {k_0}\frac{{{\ell _0}}}{{\ell '}} \end{array} \right.\)
.jpg?enablejsapi=1)
Nếu lò xo được cắt thành n phần bằng nhau.
\({{\ell }_{1}}={{\ell }_{2}}=...={{\ell }_{n}}=\frac{{{\ell }_{0}}}{2}\Rightarrow {{k}_{1}}={{k}_{2}}=....{{k}_{n}}=n{{k}_{0}}\)
+ ω, f tăng \(\sqrt{n}\) lần.
+ T giảm \(\sqrt{n}\) lần.
1.2. Ghép lò xo
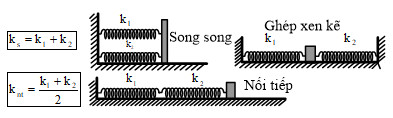
* Ghép nối tiếp: \(\frac{1}{{{k}_{nt}}}=\frac{1}{{{k}_{1}}}+\frac{1}{{{k}_{2}}}+...\)
* Ghép song song: \({{k}_{s}}={{k}_{1}}+{{k}_{2}}+...\)
* Nếu một vật có khối lượng m lần lượt liên kết với các lò xo khác nhau thì hệ thức liên hệ:
\(\left\{ \begin{array}{l} T_{nt}^2 = T_1^2 + T_2^2 + ....\\ \frac{1}{{T_s^2}} = \frac{1}{{T_1^2}} + \frac{1}{{T_2^2}} + ... \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} \frac{1}{{f_{nt}^2}} = \frac{1}{{f_1^2}} + \frac{1}{{f_2^2}} + ...\\ f_s^2 = f_2^2 + f_2^2 + ... \end{array} \right.\)
2. VÍ DỤ MINH HỌA
Ví dụ 1: Một con lắc lò xo gồm vật có khối lượng m và lò xo có độ cứng k, dao động điều hòa Nếu cắt bớt một nửa chiều dài của lò xo và giảm khối lượng m đi 8 lần thì chu kì dao động của vật sẽ
A. tăng 2 lần.
B. giảm 2 lần.
C. giảm 4 lần.
D. tăng 4 lần.
Hướng dẫn
\(k\ell =k'\ell '\Rightarrow k'=k\frac{\ell }{\ell '}=2k\Rightarrow \frac{T'}{T}=\frac{2\pi \sqrt{\frac{m'}{k'}}}{2\pi \sqrt{\frac{m}{k}}}=\sqrt{\frac{m'}{m}}\sqrt{\frac{k'}{k}}=\sqrt{\frac{1}{8}}.\sqrt{\frac{1}{8}}=\frac{1}{4}\Rightarrow \) Chọn C.
Ví dụ 2: Hai đầu A và B của lò xo gắn hai vật nhỏ có khối lượng m và 3m. Hệ có thể dao động không ma sát trên mặt phẳng ngang. Khi giữ cố định điểm C trên lò xo thì chu kì dao động của hai vật bằng nhau. Tính tỉ số CB/AB khi lò xo không biến dạng.
A. 4.
B. 1/3.
C. 0,25.
D. 3.
Hướng dẫn
.jpg)
\(1=\frac{{{T}_{AC}}}{{{T}_{CB}}}=\frac{2\pi \sqrt{\frac{{{m}_{AC}}}{{{k}_{AC}}}}}{2\pi \sqrt{\frac{{{m}_{CB}}}{{{k}_{CB}}}}}=\sqrt{\frac{1}{3}\frac{{{k}_{CB}}}{{{k}_{AC}}}}\Rightarrow AC=3CB\Rightarrow \frac{CB}{AB}=\frac{1}{4}\Rightarrow \) Chọn C.
Ví dụ 3: Biết độ dài tự nhiên của lò xo treo vật nặng là 25cm. Nếu cắt bỏ 9 cm lò xo thì chu kỳ dao động riêng của con lắc:
A. Giảm 25%.
B. Giảm 20%.
C. Giảm 18%.
D. Tăng 20%.
Hướng dẫn
\(\frac{T'}{T}=\frac{2\pi \sqrt{\frac{m}{k'}}}{2\pi \sqrt{\frac{m}{k}}}=\sqrt{\frac{k'}{k}}=\sqrt{\frac{\ell '}{\ell }}=\frac{4}{5}=80%\Rightarrow \) Giảm \(100%-80%=20%\Rightarrow \) Chọn B.
Ví dụ 4: Một lò xo đồng chất, tiết diện đều được cắt thành ba lò xo có chiều dài tự nhiên là \(\ell \) (cm), (\(\ell \)− 10) (cm) và (\(\ell \)− 30) (cm). Lần lượt gắn mỗi lò xo này (theo thứ tự trên) với vật nhỏ khối lượng m thì được ba con lắc có chu kì dao động riêng tương ứng là: 2 s; \(\sqrt{3}\) s và T. Biết độ cứng của các lò xo tỉ lệ nghịch với chiều dài tự nhiên của nó. Giá trị của T là
A. 1,00 s.
B. 1,28 s.
C. 1,41 s.
D. 1,50 s.
Hướng dẫn
Từ công thức \(T=2\pi \sqrt{\frac{m}{k}}\) và độ cứng tỉ lệ nghịch với chiều dài nên:
\(\frac{{{T}_{2}}}{{{T}_{1}}}=\sqrt{\frac{{{k}_{1}}}{{{k}_{2}}}}=\sqrt{\frac{{{\ell }_{2}}}{{{\ell }_{1}}}}=\sqrt{\frac{\ell -0,1}{\ell }}=\sqrt{1-\frac{0,1}{\ell }}\Rightarrow \frac{\sqrt{3}}{2}=\sqrt{1-\frac{0,1}{\ell }}\Rightarrow \ell =0,4\left( m \right)\)
\(\frac{{{T}_{3}}}{{{T}_{1}}}=\sqrt{\frac{{{k}_{1}}}{{{k}_{2}}}}=\sqrt{\frac{{{\ell }_{3}}}{{{\ell }_{1}}}}=\sqrt{\frac{\ell -0,3}{\ell }}=\sqrt{\frac{0,4-0,3}{0,4}}=\sqrt{\frac{1}{4}}\Rightarrow {{T}_{3}}=\frac{{{T}_{1}}}{2}=1\left( s \right)\Rightarrow \) Chọn A.
--- (Toàn bộ nội dung, chi tiết phần ví dụ minh họa tài liệu các em vui lòng xem Online hoặc Đăng nhập vào HOC247 đề tải về máy) ---
3. LUYỆN TẬP
Bài 1: Một lò xo dài 1,2 m độ cứng 120 N/m. Khi cắt lò xo đó thành 2 lò xo có chiều dài 100 cm và 20 cm thì độ cứng tương ứng lần lượt là
A. 144N/m và 720N/m.
B. 100 N/m và 20 N/m.
C. 720 N/m và 144 N/m.
D. 20 N/m và 100 N/m.
Bài 2: Con lắc lò xo gồm vật nặng treo dưới lò xơ dài, có chu kỳ dao động là T. Nếu lò xo bị cắt bớt 2/3 chiều dài thì chu kỳ dao động của con lắc mới là:
A. 3T
B. 0,5T\(\sqrt{6}.\)
C. T/3.
D. T/\(\sqrt{3}\)
Bài 3: Quả cầu m gắn vào lò xo có độ cứng k thì nó dao động với chu kỳ T. Hỏi phải cắt lò xo trên thành bao nhiêu phần bằng nhau để khi treo quả cầu vào mỗi phần thì chu kỳ dao động có giá trị T’ = T/2
A. Cắt làm 4 phần.
B. cắt làm 6 phần.
C. cắt làm 2 phần.
D. cắt làm 8 phần.
Bài 4: Quả cầu m gắn vào lò xo có độ cứng k thì nó dao động với chu kỳ T. cắt lò xo trên thành 3 phần có chiều dài theo đúng tỉ lệ 1:2:3. Lấy phần ngắn nhất và treo quả cầu vào thì chu kỳ dao động có giá trị là
A. T/3.
B. \(T/\sqrt{6}.\)
C. \(T/\sqrt{3}\)
D. T/6.
Bài 5: Một con lắc lò xo có độ dài 120 cm. cắt bớt chiều dài thì chu kỳ dao động mới chỉ bằng 90% chu kỳ dao động ban đầu. Tính độ dài mới.
A. 148,148 cm.
B. 133,33 cm.
C. 108 cm.
D. 97,2 cm.
Bài 6: Con lắc lò xo dao động điều hòa không ma sát theo phương nằm ngang với biên độ A. Đúng lúc vật đi qua vị trí cân bằng, người ta giữ chặt lò xo tại điểm cách đầu cố định của nó một đoạn bằng 60% chiều dài tự nhiên của lò xo. Hỏi sau đó con lắc dao động với biên độ A' bằng bao nhiêu lần biên độ A lúc đầu?
A. \(2/\sqrt{2}\).
B. \(\sqrt{8/3}\).
C.\)\sqrt{3/8}\) .
D. \)\left( 0,2\sqrt{10} \right)\).
Bài 7: Con lắc lò xo nằm ngang dao động điều hòa với biên độ A. Khi vật nặng chuyển động qua vị trí cân bằng thì giữ cố định điểm cách điểm cố định một đoạn bằng 1/4 chiều dài tự nhiên của lò xo. Vật sẽ tiếp tục dao động với biên độ bằng:
A.\(A/\sqrt{2}.\)
B. 0,5A.
C. A/2.
D. \(A\sqrt{2}\).
Bài 8: Con lắc lò xo nằm ngang daọ động điều hòa với biên độ A. Khi vật nặng chuyển động qua vị trí cân bằng thì giữ cố định điểm cách điểm cố định một đoạn bằng 1/3 chiều dài tự nhiên của lò xo. Vật sẽ tiếp tục dao động với biên độ bằng
A. \(A/\sqrt{2}.\)
B. 0,5A\(\sqrt{3}\) .
C. A/2.
D. \(\sqrt{6}\) A/3.
Bài 9: Một con lắc lò xo treo thẳng đứng dao động điều hòa với biên độ A và tần số f. Khi vật đi qua vị trí cân bằng thì người ta giữ cố định điểm chính giữa của lò xo lại. Bắt đầu từ thời điểm đó vật sẽ dao động điều hòa với
A. biên độ là A/\(\sqrt{2}\) và tần số f \(\sqrt{2}\).
B. biên độ là A/\(\sqrt{2}\) và tần số f\(\sqrt{2}\) .
C. biên độ là A\(\sqrt{2}\) và tần số f/\(\sqrt{2}\).
D. biên độ là A\(\sqrt{2}\)và tần số f\(\sqrt{2}\) .
Bài 10: Một con lắc lò xo dao động điều hòa trên mặt phẳng ngang. Từ vị trí cân bằng người ta kéo vật ra 8 cm rồi thả nhẹ, khi vật cách vị trí cân bằng 4 cm thì người ta giữ cố định điểm chính giữa của lò xo. Tính biên độ dao động mới của vật
A. 4 \(\sqrt{2}\)cm.
B. 4 cm
C. \(6\sqrt{3}cm\)
D. 2\(\sqrt{7}\) cm.
Bài 11: Con lắc lò xo dao động điều hòa theo phương ngang với biên độ A. Đúng lúc con lắc qua vị trí có động năng bằng thế năng và đang dãn thì người ta cố định một điểm chính giữa của lò xo, kết quả làm con lắc dao động điều hòa với biên độ A’. Hãy lập tỉ lệ giữa biên độ A và biên độ A
A. 2/\(\sqrt{2}\).
B. \(\sqrt{8/3}\) .
C. \(\sqrt{3/8}\) .
D. \(\left( 2\sqrt{6} \right)/3\).
Bài 12: Con lắc lò xo dao động điều hòa theo phương ngang với biên độ A. Đúng lúc con lắc qua vị trí lò xo dãn nhiều nhất người ta cố định một điểm chính giữa của lò xo, kết quả làm con lắc dao động điều hòa với biên độ A’. Hãy lập tỉ lệ giữa biên độ A và biên độ A’.
A. 2/\(\sqrt{2}\).
B. \(\sqrt{8/3}\) .
C. \(\sqrt{3/8}\).
D. 2
Bài 13: Con lắc gồm lò xo có chiều dài 20 cm và vật nặng khối lượng m, dao động điều hòa với tần số 2 Hz. Nếu cắt bỏ lò xo đi một đoạn 15 cm thì con lắc sẽ dao động điều hòa với tần số là
A. 4 Hz.
B. 2/3 Hz.
C. 1,5 Hz.
D. 6 Hz.
Bài 14: Một lò xo có chiều dài tự nhiên 10cm, khối lượng không đáng kể, đặt trên mặt phẳng ngang. Hai vật có khối lượng m1 = 30g và m2 = 50g gắn lần lượt vào hai đầu A và B của lò xo. Giữ cố định 1 điểm C nằm trong khoảng giữa lò xo và cho 2 vật dao động điều hòa theo phương ngang thì thấy chu kì dao động 2 vật bằng nhau. Khoảng cách AC là
A. 4cm.
B. 3,75cm.
C. 6,25cm
D. 6cm
Bài 15: Một con lắc lò xo dao động điều hòa trên mặt phẳng ngang với chu kỳ T và biên độ A. Khi t = 0 vật có li độ x = A. Đến thời điểm t = 19T + T/12 người ta giữ cố định 20% chiều dài của lò xo. Tính biên độ dao động mới của vật?
A. \(A\sqrt{17}/5.\)
B. A/2.
C. \(3A\sqrt{2}/5\)
D. \(A\sqrt{7}/4\).
ĐÁP ÁN
|
1.A |
2.D |
3.A |
4.B |
5.D |
6.D |
7.B |
8.D |
9.A |
10.D |
|
11.D |
12.D |
13.A |
14.C |
15.A |
|
|
|
|
|
Trên đây là một đoạn trích dẫn nội dung Phương pháp giải bài toán liên quan đến cắt ghép lò xo môn Vật Lý 12 năm 2021-2022. Để xem thêm nhiều tài liệu tham khảo hữu ích khác của các chức năng chọn xem trực tuyến hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.
Hy vọng tài liệu này sẽ giúp các em học tập tốt và đạt được thành tích cao trong học tập.