Vß╗øi mß╗źc ─æ├Łch c├│ th├¬m t├Āi liß╗ću gi├║p c├Īc em hß╗Źc sinh lß╗øp 12 ├┤n tß║Łp HOC247 giß╗øi thiß╗ću ─æß║┐n c├Īc em t├Āi liß╗ću C├Īc phŲ░ŲĪng ph├Īp biß╗āu diß╗ģn dao ─æß╗Öng ─æiß╗üu h├▓a v├Ā c├Īc ─æß║Īi lŲ░ß╗Żng ─æß║Ęc trŲ░ng m├┤n Vß║Łt L├Į 12 n─ām 2021-2022 ─æŲ░ß╗Żc HOC247 bi├¬n tß║Łp v├Ā tß╗Ģng hß╗Żp vß╗øi phß║¦n ─æß╗ü v├Ā ─æ├Īp ├Īn, lß╗Øi giß║Żi chi tiß║┐t gi├║p c├Īc em tß╗▒ luyß╗ćn tß║Łp l├Ām ─æß╗ü.
Hi vß╗Źng t├Āi liß╗ću n├Āy sß║Į c├│ ├Łch cho c├Īc em, ch├║c c├Īc em c├│ kß║┐t quß║Ż hß╗Źc tß║Łp tß╗æt!
1. T├ōM Tß║«T L├Ø THUYß║ŠT
1.1. C├Īc b├Āi to├Īn y├¬u cß║¦u sß╗Ł dß╗źng linh hoß║Īt c├Īc phŲ░ŲĪng tr├¼nh
1.1.1. C├Īc phŲ░ŲĪng tr├¼nh phß╗ź thuß╗Öc thß╗Øi gian:
\(x=A\cos \left( \omega t+\varphi \right)\)
\(v=x'=-\omega A\sin \left( \omega t+\varphi \right)\)
\(a=v'=-{{\omega }^{2}}A\cos \left( \omega t+\varphi \right)\)
\(F=ma=-m{{\omega }^{2}}A\cos \left( \omega t+\varphi \right)\)
\({{W}_{t}}=\frac{k{{x}^{2}}}{2}=\frac{m{{\omega }^{2}}{{A}^{2}}}{2}{{\cos }^{2}}\left( \omega t+\varphi \right)=\frac{m{{\omega }^{2}}{{A}^{2}}}{4}\left[ 1+\cos \left( 2\omega t+2\varphi \right) \right]\)
\({{W}_{d}}=\frac{m{{v}^{2}}}{2}=\frac{m{{\omega }^{2}}{{A}^{2}}}{2}{{\sin }^{2}}\left( \omega t+\varphi \right)=\frac{m{{\omega }^{2}}{{A}^{2}}}{4}\left[ 1-\cos \left( 2\omega t+2\varphi \right) \right]\)
W = Wt + Wd \(=\frac{m{{\omega }^{2}}{{A}^{2}}}{2}=\frac{k{{A}^{2}}}{2}\)
PhŲ░ŲĪng ph├Īp chung: ─Éß╗æi chiß║┐u phŲ░ŲĪng tr├¼nh cß╗¦a b├Āi to├Īn vß╗øi phŲ░ong tr├¼nh tß╗Ģng qu├Īt ─æß╗ā t├¼m c├Īc ─æß║Īi lŲ░ß╗Żng.
1.1.2. C├Īc phŲ░ŲĪng tr├¼nh ─æß╗Öc lß║Łp vß╗øi thß╗Øi gian
\(\left\{ \begin{array}{l}
{x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2}\\
a = - {\omega ^2}x\\
F = m{\omega ^2}x = - kx\\
k = m{\omega ^2}
\end{array} \right.;W = {W_t} + {W_d} = \frac{{k{x^2}}}{2} + \frac{{m{v^2}}}{2} = \frac{{m{\omega ^2}{A^2}}}{2} = \frac{{k{A^2}}}{2}\)
PhŲ░ŲĪng ph├Īp chung: Biß║┐n ─æß╗Ģi vß╗ü phŲ░ŲĪng tr├¼nh hoß║Ęc hß╗ć phŲ░ŲĪng tr├¼nh c├│ chß╗®a ─æß║Īi lŲ░ß╗Żng cß║¦n t├¼m v├Ā ─æß║Īi lŲ░ß╗Żng ─æ├Ż biß║┐t.
1.2. C├Īc b├Āi to├Īn sß╗Ł dß╗źng v├▓ng tr├▓n lŲ░ß╗Żng gi├Īc
Kinh nghiß╗ćm cho thß║źy, nhß╗»ng b├Āi to├Īn kh├┤ng li├¬n quan ─æß║┐n hŲ░ß╗øng cß╗¦a dao ─æß╗Öng ─æiß╗üu h├▓a hoß║Ęc li├¬n quan vß║Łn tß╗æc hoß║Ęc gia tß╗æc th├¼ n├¬n giß║Żi b├Āi to├Īn bß║▒ng c├Īch sß╗Ł dß╗źng c├Īc phŲ░ŲĪng tr├¼nh; c├▓n nß║┐u li├¬n quan ─æß║┐n hŲ░ß╗øng th├¼ khi sß╗Ł dß╗źng v├▓ng tr├▓n lŲ░ß╗Żng gi├Īc sß║Į cho lß╗Øi giß║Żi ngß║»n gß╗Źn!
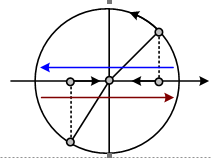
Ta ─æ├Ż biß║┐t, h├¼nh chiß║┐u cß╗¦a chuyß╗ān ─æß╗Öng tr├▓n ─æß╗üu tr├¬n mß╗Öt trß╗źc nß║▒m trong mß║Ęt phß║│ng quß╗╣ ─æß║Īo biß╗āu diß╗ģn mß╗Öt dao ─æß╗Öng ─æiß╗üu h├▓a: \(x = A\cos \left( {\omega t + \varphi } \right)\)
+ ß╗× nß╗Ła tr├¬n v├▓ng tr├▓n th├¼ h├¼nh chiß║┐u ─æi theo chiß╗üu ├óm, c├▓n ß╗¤ dŲ░ß╗øi th├¼ h├¼nh chiß║┐u ─æi theo chiß╗üu dŲ░ŲĪng!
1.2.1. Chuyß╗ān ─æß╗Öng tr├▓n ─æß╗üu v├Ā dao ─æß╗Öng ─æiß╗üu ho├Ā
PhŲ░ŲĪng ph├Īp chung:
Dß╗▒a v├Āo mß╗æi quan hß╗ć giß╗»a c├Īc ─æß║Īi lŲ░ß╗Żng trong dao ─æß╗Öng ─æiß╗üu h├▓a v├Ā trong chuyß╗ān ─æß╗Öng tr├▓n ─æß╗üu.
\(x = A\cos \left( {\omega t + \varphi } \right)\) = H├¼nh chiß║┐u cß╗¦a C─ÉT─É: b├Īn k├Łnh bß║▒ng A, tß║¦n sß╗æ g├│c Žē, tß╗æc ─æß╗Ö d├Āi \({v_T} = \omega A.\)
\({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = A \Leftrightarrow {\left( {\frac{x}{A}} \right)^2} + {\left( {\frac{v}{{\omega A}}} \right)^2} = 1 \Leftrightarrow {\left( {\frac{x}{A}} \right)^2} + {\left( {\frac{v}{{{v_T}}}} \right)^2} = 1\)
1.2.2. Khoß║Żng th├▓i gian ─æß╗ā v├®c tŲĪ vß║Łn tß╗æc v├Ā gia tß╗æc c├╣ng chiß╗üu, ngŲ░ß╗Żc chiß╗üu.
PhŲ░ŲĪng ph├Īp chung:
Viß║┐t phŲ░ŲĪng tr├¼nnh dŲ░ß╗øi dß║Īng: \(x = A\cos \left( {\omega t + \varphi } \right);\phi = \left( {\omega t + \varphi } \right)\) rß╗ōi phß╗æi hß╗Żp vß╗øi v├▓ng tr├▓n lŲ░ß╗Żng gi├Īc.
Ch├║ ├Į rß║▒ng \(\overrightarrow v \) lu├┤n c├╣ng hŲ░ß╗øng vß╗øi hŲ░ß╗øng chuyß╗ān ─æß╗Öng, \(\overrightarrow a \) lu├┤n hŲ░ß╗øng vß╗ü vß╗ŗ tr├Ł c├ón bß║▒ng.
1.2.3. T├¼m li ─æß╗Ö v├Ā hŲ░ß╗øng chuyß╗ān ─æß╗Öng PhŲ░ŲĪng ph├Īp chung:
Vß║Łt chuyß╗ān ─æß╗Öng vß╗ü vß╗ŗ tr├Ł c├ón bß║▒ng l├Ā nhanh dß║¦n (kh├┤ng ─æß╗üu) v├Ā chuyß╗ān ─æß╗Öng ra xa vß╗ŗ tr├Ł c├ón bß║▒ng l├Ā chß║Łm dß║¦n (kh├┤ng ─æß╗üu).
C├Īch 1:
\(\left\{ \begin{array}{l}
x = A\cos \left( {\omega t + \varphi } \right)\\
v = x' = - \omega A\sin \left( {\omega t + \varphi } \right)
\end{array} \right. \to \left\{ \begin{array}{l}
{x_{\left( {t0} \right)}} = A\cos \left( {\omega .{t_0} + \varphi } \right)\\
{v_{\left( {{t_0}} \right)}} = - \omega A\sin \left( {\omega .{t_0} + \varphi } \right)
\end{array} \right.\)
+ \({v_{\left( {{t_0}} \right)}}\) > 0: Vß║Łt ─æi theo chiß╗üu dŲ░ŲĪng (x ─æang t─āng).
+ \({v_{\left( {{t_0}} \right)}}\) < 0: Vß║Łt ─æi theo chiß╗üu ├óm (x ─æang giß║Żm),
C├Īch 2:
X├Īc ─æß╗ŗnh vß╗ŗ tr├Ł tr├¬n v├▓ng lŲ░ß╗Żng gi├Īc ß╗¤ thß╗Øi ─æiß╗ām \({t_0}:\phi = \omega .{t_0} + \varphi .\)
Nß║┐u thuß╗Öc nß╗Ła tr├¬n v├▓ng tr├▓n lŲ░ß╗Żng gi├Īc th├¼ h├¼nh chiß║┐u chuyß╗ān ─æß╗Öng theo chiß╗üu ├óm (li ─æß╗Ö ─æang giß║Żm).
Nß║┐u thuß╗Öc nß╗Ła dŲ░ß╗øi v├▓ng tr├▓n lŲ░ß╗Żng gi├Īc th├¼ h├¼nh chiß║┐u chuyß╗ān ─æß╗Öng theo chiß╗üu dŲ░ŲĪng (li ─æß╗Ö ─æang t─āng).
Li độ dao động điều hòa: \(x = A\cos {\Phi _{\left( {{t_0}} \right)}}\)
Vß║Łn tß╗æc dao ─æß╗Öng ─æiß╗üu h├▓a: v = x' = \( - \omega in{\Phi _{\left( {{t_0}} \right)}}\)
---(─Éß╗ā xem ─æß║¦y ─æß╗¦, chi tiß║┐t cß╗¦a t├Āi liß╗ću vui l├▓ng xem tß║Īi online hoß║Ęc ─æ─āng nhß║Łp ─æß╗ā tß║Żi vß╗ü m├Īy)---
2. B├ĆI Tß║¼P MINH Hß╗īA
B├Āi 1: Mß╗Öt chß║źt ─æiß╗ām dao ─æß╗Öng ─æiß╗üu h├▓a c├│ phŲ░ŲĪng tr├¼nh vß║Łn tß╗æc l├Ā \(v = 3\pi \cos 3\pi t\) (cm/s). Gß╗æc tß╗Źa ─æß╗Ö ß╗¤ vß╗ŗ tr├Ł c├ón bß║▒ng. Mß╗æc thß╗Øi gian ─æŲ░ß╗Żc chß╗Źn v├Āo l├║c chß║źt ─æiß╗ām c├│ li ─æß╗Ö v├Ā vß║Łn tß╗æc l├Ā:
A. x = 2cm, v = 0.
B. x = 0, v = 3ŽĆ cm/s.
C. x= ŌłÆ 2 cm, v = 0.
D. x = 0, v = ŌłÆ ŽĆ cm/s.
HŲ░ß╗øng dß║½n
─Éß╗æi chiß║┐u vß╗øi c├Īc phŲ░ŲĪng tr├¼nh tß╗Ģng qu├Īt ta t├Łnh ─æŲ░ß╗Żc:
\(\left\{ \begin{array}{l} x = A\cos \left( {3\pi t + \varphi } \right)\\ v = x' = - 3\pi A\sin \left( {3\pi t + \varphi } \right) = 3\pi A\cos \left( {3\pi t + \varphi + \frac{\pi }{2}} \right) \end{array} \right. \Rightarrow \left\{ \begin{array}{l} \varphi = - \frac{\pi }{2}\\ A = 1\left( {cm} \right) \end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l} {x_{\left( 0 \right)}} = 1\cos \left( {3\pi .0 - \frac{\pi }{2}} \right) = 0\\ {v_{\left( 0 \right)}} = 3\pi \cos \left( {3\pi .0} \right) = 3\pi \left( {cm/s} \right) \end{array} \right. \Rightarrow \) Chß╗Źn B.
B├Āi 2: Mß╗Öt vß║Łt dao ─æß╗Öng ─æiß╗üu ho├Ā, khi vß║Łt c├│ li ─æß╗Ö x1 = 4 (cm) th├¼ vß║Łn tß╗æc \({{v}_{1}}=-40\pi \sqrt{3}\) (cm/s) v├Ā khi vß║Łt c├│ li ─æß╗Ö \({{x}_{2}}=4\sqrt{2}\) (cm) thß╗ē vß║Łn tß╗æc \({{v}_{1}}=-40\pi \sqrt{2}\left( cm/s \right)\) (cm/s). ─Éß╗Öng n─āng biß║┐n thi├¬n vß╗øi chu kß╗│
A. 0,1 s. B. 0,8 s. C. 0,2 s. D. 0,4 s.
HŲ░ß╗øng dß║½n
├üp dß╗źng c├┤ng thß╗®c: \({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2}\)
\(\left\{ \begin{array}{l} {A^2} = {4^2} + \frac{{{{\left( { - 40\pi \sqrt 3 } \right)}^2}}}{{{\omega ^2}}}\\ {A^2} = {\left( {4\sqrt 2 } \right)^2} + \frac{{{{\left( { - 40\pi \sqrt 2 } \right)}^2}}}{{{\omega ^2}}} \end{array} \right. \Rightarrow \omega = 10\pi \left( {rad/s} \right) \Rightarrow T = \frac{{2\pi }}{\omega } = 0,2\left( s \right)\)
─Éß╗Öng n─āng v├Ā thß║┐ n─āng ─æß╗üu biß║┐n ─æß╗Ģi tuß║¦n ho├Ān theo thß╗Øi gian vß╗øi chu kß╗│ l├Ā:
\(T' = \frac{T}{2} = 0,1\left( s \right) \Rightarrow \) Chß╗Źn A.
B├Āi 3: Mß╗Öt chß║źt ─æiß╗ām chuyß╗ān ─æß╗Öng tr├▓n ─æß╗üu tr├¬n ─æŲ░ß╗Øng tr├▓n t├óm O b├Īn k├Łnh 10 cm vß╗øi tß╗æc ─æß╗Ö g├│c 5 rad/s. H├¼nh chiß║┐u cß╗¦a chß║źt ─æiß╗ām l├¬n trß╗źc Ox nß║▒m trong mß║Ęt phß║│ng quß╗╣ ─æß║Īo c├│ tß╗æc ─æß╗Ö cß╗▒c ─æß║Īi l├Ā
A. 15 cm/s.
B. 50 cm/s.
C. 250 cm/s.
D. 25 cm/s.
HŲ░ß╗øng dß║½n
* Mß╗Öt chß║źt ─æiß╗ām chuyß╗ān ─æß╗Öng tr├▓n ─æß╗üu tr├¬n ─æŲ░ß╗Øng tr├▓n b├Īn k├Łnh R vß╗øi tß╗æc ─æß╗Ö g├│c \(\omega \) th├¼ h├¼nh chiß║┐u cß╗¦a n├│ tr├¬n mß╗Öt trß╗źc nß║▒m trong mß║Ęt phß║│ng quß╗╣ ─æß║Īo sß║Į dao ─æß╗Öng ─æiß╗üu h├▓a vß╗øi bi├¬n ─æß╗Ö ─æ├║ng bß║▒ng R v├Ā tß║¦n sß╗æ g├│c ─æ├║ng bß║▒ng \(\omega \)
* H├¼nh chiß║┐u cß╗¦a chß║źt ─æiß╗ām l├¬n trß╗źc Ox nß║▒m trong mß║Ęt phß║│ng quß╗╣ ─æß║Īo dao ─æß╗Öng ─æiß╗üu h├▓a vß╗øi bi├¬n ─æß╗Ö A = 10 cm v├Ā tß║¦n sß╗æ g├│c \(\omega \) = 5 rad/s => tß╗æc ─æß╗Ö cß╗▒c ─æß║Īi l├Ā \({{v}_{\max }}=\omega A\) = 50 cm/s => Chß╗Źn B.
B├Āi 4: Mß╗Öt chß║źt ─æiß╗ām dao ─æß╗Öng ─æiß╗üu h├▓a tr├¬n trß╗źc Ox c├│ phŲ░ŲĪng tr├¼nh x = Acos(5ŽĆt + ŽĆ/2) (cm). V├®c tŲĪ vß║Łn tß╗æc v├Ā v├®c tŲĪ gia tß╗æc sß║Į c├│ c├╣ng chiß╗üu dŲ░ŲĪng cß╗¦a trß╗źc Ox trong khoß║Żng thß╗Øi gian n├Āo (kß╗ā tß╗½ thß╗Øi ─æiß╗ām ban ─æß║¦u t = 0) sau ─æ├óy?
A. 0,2 s < t < 0,3 s.
B. 0,0s < t < 0,l s.
C. 0,3 s < t < 0,4 s.
D. 0,1 s < t <0,2 s.
HŲ░ß╗øng dß║½n
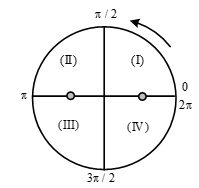
Muß╗æn v > 0, a > 0 th├¼ chß║źt ─æiß╗ām chuyß╗ān ─æß╗Öng tr├▓n ─æß╗üu phß║Żi thuß╗Öc g├│c (III) (Vß║Łt ─æi tß╗½ x = ŌłÆ A ─æß║┐n x = 0):
\(\pi <5\pi t+\frac{\pi }{2}<\frac{3\pi }{2}\Rightarrow 0,1s
B├Āi 5: Mß╗Öt vß║Łt dao ─æß╗Öng ─æiß╗üu h├▓a c├│ phŲ░ŲĪng tr├¼nh li ─æß╗Ö \(x=2\sqrt{2}\cos \left( 10\pi t+3\pi /4 \right)\) , trong ─æ├│ x t├Łnh bß║▒ng xentim├®t (cm) v├Ā t t├Łnh bß║▒ng gi├óy (s). L├║c t = 0 s vß║Łt c├│
A. li ─æß╗Ö ŌłÆ 2 cm v├Ā ─æang ─æi theo chiß╗üu ├óm.
B. li ─æß╗Ö ŌłÆ 2 cm v├Ā ─æang ─æi theo chiß╗üu dŲ░ŲĪng.
C. li ─æß╗Ö +2 cm v├Ā ─æang ─æi theo chiß╗üu dŲ░ŲĪng.
D. li ─æß╗Ö +2 cm v├Ā ─æang ─æi theo chiß╗üu ├óm.
HŲ░ß╗øng dß║½n
\(\left\{ \begin{array}{l}
{x_{\left( 0 \right)}} = 2\sqrt 2 \cos \left( {10\pi .0 + \frac{{3\pi }}{4}} \right) = - 2\left( {cm} \right)\\
{v_{\left( 0 \right)}} = x' = - 20\pi \sqrt 2 \sin \left( {10\pi .0 + \frac{{3p}}{4}} \right) < 0
\end{array} \right. \Rightarrow \) Chß╗Źn A.
B├Āi 6: Mß╗Öt chß║źt ─æiß╗ām chuyß╗ān ─æß╗Öng tr├▓n ─æß╗üu vß╗øi tß╗æc ─æß╗Ö 1 m/s tr├¬n ─æŲ░ß╗Øng tr├▓n ─æŲ░ß╗Øng k├Łnh 0,5 m. H├¼nh chiß║┐u MŌĆÖ cß╗¦a ─æiß╗ām M l├¬n ─æŲ░ß╗Øng k├Łnh cß╗¦a ─æŲ░ß╗Øng Ų░├▓n dao ─æß╗Öng ─æiß╗üu h├▓a. Biß║┐t tß║Īi thß╗Øi ─æiß╗ām t = t0, MŌĆÖ ─æi qua vß╗ŗ tr├Ł c├ón bß║▒ng theo chiß╗üu ├óm. Hß╗Åi trŲ░ß╗øc thß╗Øi ─æiß╗ām v├Ā sau thß╗Øi ─æiß╗ām t0 l├Ā 8,5 s h├¼nh chiß║┐u MŌĆÖ ß╗¤ vß╗ŗ tr├Ł n├Āo v├Ā ─æi theo chiß╗üu n├Āo?
HŲ░ß╗øng dß║½n
Bi├¬n ─æß╗Ö v├Ā tß║¦n sß╗æ g├│c lß║¦n lŲ░ß╗Żt l├Ā: \(\left\{ \begin{array}{l} A = \frac{{50}}{2} = 25\left( {cm} \right)\\ \omega = \frac{{{v_T}}}{A} = - \frac{{100}}{{25}} = 4\left( {rad/s} \right) \end{array} \right.\)
G├│c cß║¦n qu├®t: \(\Delta \Phi = \omega \Delta t = 34\,rad \approx 10,8225 = 5.2\pi + 0,08225\pi \)
+ ─Éß╗ā t├¼m trß║Īng th├Īi ß╗¤ thß╗Øi ─æiß╗ām t = t0 ŌłÆ 8,5 s ta chß╗ē cß║¦n qu├®t theo chiß╗üu ├óm g├│c 0,8225ŽĆ:
\(x=25\cos \left( 0,3225\pi \right)\) \(\approx 13,2\) > 0 . L├║c n├Āy chß║źt ─æiß╗ām nß║▒m ß╗¤ nß╗Ła dŲ░ß╗øi n├¬n h├¼nh chiß║┐u ─æi theo chiß╗üu dŲ░ŲĪng.
+ ─Éß╗ā t├¼m trß║Īng th├Īi ß╗¤ thß╗Øi ─æiß╗ām t = t0 + 8,5 s ta chß╗ē cß║¦n qu├®t theo chiß╗üu dŲ░ŲĪng g├│c 0,8225ŽĆ. Suy ra: \(x=-25\cos 0,3225\pi \approx -13,2cm\) < 0. L├║c n├Āy chß║źt ─æiß╗ām nß║▒m ß╗¤ nß╗Ła dŲ░ß╗øi n├¬n h├¼nh chiß║┐u ─æi theo chiß╗üu dŲ░ŲĪng.
3. LUYỆN TẬP
B├Āi 1: Mß╗Öt con lß║»c l├▓ xo, gß╗ōm l├▓ xo nhß║╣ c├│ ─æß╗Ö cß╗®ng 50 (N/m), vß║Łt c├│ khß╗æi lŲ░ß╗Żng 2 (kg), dao ─æß╗Öng ─æiß╗üu ho├Ā. Tß║Īi thß╗Øi ─æiß╗ām vß║Łt c├│ li ─æß╗Ö 3 cm th├¼ n├│ c├│ vß║Łn tß╗æc 15 (cm/s). X├Īc ─æß╗ŗnh bi├¬n ─æß╗Ö.
A. 5 cm. B. 6 cm. C. 9 cm. D. 10 cm.
B├Āi 2: Mß╗Öt con lß║»c l├▓ xo gß╗ōm l├▓ xo c├│ ─æß╗Ö cß╗®ng 2,5 N/m v├Ā vi├¬n bi c├│ khß╗æi lŲ░ß╗Żng 0,1 kg dao ─æß╗Öng ─æiß╗üu h├▓a. Tß║Īi thß╗Øi ─æiß╗ām t, vß║Łn tß╗æc v├Ā gia tß╗æc cß╗¦a vi├¬n bi lß║¦n lŲ░ß╗Żt l├Ā 10 cm/s v├Ā 0,5 m/s2. Bi├¬n ─æß╗Ö dao ─æß╗Öng cß╗¦a vi├¬n bi l├Ā
A. 16cm B. 4cm C. 4 cm. D. 10 cm.
B├Āi 3: Mß╗Öt vß║Łt dao ─æß╗Öng ─æiß╗üu ho├Ā, vß║Łn tß╗æc cß╗¦a vß║Łt khi ─æi qua vß╗ŗ tr├Ł c├ón bß║▒ng c├│ ─æß╗Ö lß╗øn 20ŽĆ (cm/s) v├Ā gia tß╗æc cß╗▒c ─æß║Īi cß╗¦a vß║Łt l├Ā 200ŽĆ2 (cm/s2). T├Łnh bi├¬n ─æß╗Ö dao ─æß╗Öng.
A. 2 cm. B. 10 cm. C. 20 cm. D. 4 cm.
B├Āi 4: Mß╗Öt vß║Łt dao ─æß╗Öng ─æiß╗üu h├▓a dß╗Źc theo trß╗źc x quanh gß╗æc tß╗Źa ─æß╗Ö vß╗øi phŲ░ŲĪng tr├¼nh x = Acos(4ŽĆt + Žå) vß╗øi t t├Łnh bß║▒ng s. Khi pha dao ─æß╗Öng l├Ā ŽĆ th├¼ gia tß╗æc cß╗¦a vß║Łt l├Ā 8 (m/s2). Lß║źy ŽĆ2 = 10. T├Łnh bi├¬n ─æß╗Ö dao ─æß╗Öng.
A. 5 cm. B. 10 cm. C. 20 cm. D. 4 cm.
B├Āi 5: Mß╗Öt vß║Łt dao ─æß╗Öng ─æiß╗üu h├▓a vß╗øi bi├¬n ─æß╗Ö 4 cm. Khi vß║Łt c├│ li ─æß╗Ö 2 cm th├¼ vß║Łn tß╗æc l├Ā 1 m/s. Tß║¦n sß╗æ dao ─æß╗Öng l├Ā:
A. 3 Hz. B. 1 Hz. C. 4,6 Hz. D. 1,2 Hz.
B├Āi 6: Mß╗Öt vß║Łt dao ─æß╗Öng ─æiß╗üu h├▓a trong nß╗Ła chu kß╗│ ─æi ─æŲ░ß╗Żc qu├Żng ─æŲ░ß╗Øng 10 cm. Khi vß║Łt c├│ li ─æß╗Ö 3 cm th├¼ c├│ vß║Łn tß╗æc 16ŽĆ cm/s. Chu kß╗│ dao ─æß╗Öng cß╗¦a vß║Łt l├Ā:
A. 0,5s B. l,6s C. 1 s D. 2s
B├Āi 7: Mß╗Öt vß║Łt dao ─æß╗Öng ─æiß╗üu h├▓a tr├¬n trß╗źc Ox, xung quanh vß╗ŗ tr├Ł c├ón bß║▒ng l├Ā g├┤c tß╗Źa ─æß╗Ö. Gia tß╗æc cß╗¦a vß║Łt phß╗ź thuß╗Öc v├Āo li ─æß╗Ö x theo phŲ░ŲĪng tr├¼nh: a = ŌłÆ 400ŽĆ2x. Sß╗æ dao ─æß╗Öng to├Ān phß║¦n vß║Łt thß╗▒c hiß╗ćn ─æŲ░ß╗Żc trong mß╗Śi gi├óy l├Ā
A. 20. B. 10. C. 40. D. 5.
B├Āi 8: Mß╗Öt con lß║»c l├▓ xo gß╗ōm vß║Łt nhß╗Å c├│ khß╗æi lŲ░ß╗Żng 0,25 (kg) v├Ā mß╗Öt l├▓ xo nhß║╣ c├│ ─æß╗Ö cß╗®ng 100ŽĆ2 (N/m), dao ─æß╗Öng ─æiß╗üu h├▓a dß╗Źc theo trß╗źc Ox. Khoß║Żng thß╗Øi gian giß╗»a hai lß║¦n li├¬n tiß║┐p ─æß╗Ö lß╗øn vß║Łn tß╗æc cß╗¦a vß║Łt cß╗▒c ─æß║Īi l├Ā
A. 0,1 (s). B. 0,05 (s). C. 0,025 (s). D. 0,075 (s).
B├Āi 9: Mß╗Öt dao ─æß╗Öng ─æiß╗üu h├▓a, khi vß║Łt c├│ li ─æß╗Ö 3 cm th├¼ tß╗æc ─æß╗Ö cß╗¦a n├│ l├Ā 15 cm/s, v├Ā khi vß║Łt c├│ li ─æß╗Ö cm th├¼ tß╗æc ─æß╗Ö cm/s. Tß╗æc ─æß╗Ö cß╗¦a vß║Łt khi ─æi qua vß╗ŗ tr├Ł c├ón bß║▒ng l├Ā
A. 20 (cm/s). B. 25 (cm/s). C. 50 (cm/s). D. 30 (cm/s).
B├Āi 10: Mß╗Öt vß║Łt dao ─æß╗Öng ─æiß╗üu h├▓a khi c├│ li ─æß╗Ö x1 = 2 (cm) th├¼ vß║Łn tß╗æc (cm/s), khi c├│ li ─æß╗Ö (cm) th├¼ c├│ vß║Łn tß╗æc (cm/s). Bi├¬n ─æß╗Ö v├Ā tß║¦n sß╗æ dao ─æß╗Öng cß╗¦a vß║Łt l├Ā
A. 8 cm v├Ā 2 Hz.
B. 4 cm v├Ā 1 Hz.
C. 4 cm v├Ā 2Hz.
D. 4 cm v├Ā 1Hz.
B├Āi 11: Mß╗Öt chß║źt ─æiß╗ām dao ─æß╗Öng ─æiß╗üu h├▓a tr├¬n trß╗źc Ox. Khi chß║źt ─æiß╗ām ─æi qua vß╗ŗ tr├Ł c├ón bß║▒ng th├¼ tß╗æc ─æß╗Ö cß╗¦a n├│ l├Ā 10 cm/s. Khi chß║źt ─æiß╗ām c├│ tß╗æc ─æß╗Ö l├Ā 5 cm/s th├¼ gia tß╗æc cß╗¦a n├│ c├│ ─æß╗Ö lß╗øn l├Ā cm/s2. Bi├¬n ─æß╗Ö dao ─æß╗Öng cß╗¦a chß║źt ─æiß╗ām l├Ā
A. 5 cm. B. 4cm. C. 10 cm. D. 8 cm.
B├Āi 12: Mß╗Öt vß║Łt dao ─æß╗Öng ─æiß╗üu h├▓a theo phŲ░ŲĪng tr├¼nh: x = 2,5cos10ŽĆt (cm) (vß╗øi t ─æo bß║▒ng gi├óy). Tß╗æc ─æß╗Ö trung b├¼nh cß╗¦a chuyß╗ān ─æß╗Öng trong mß╗Öt chu k├¼ l├Ā
A. 50 cm/s. B. 25 cm/s. C. 0. D. 15 cm/s.
B├Āi 13: Mß╗Öt vß║Łt dao ─æß╗Öng ─æiß╗üu h├▓a c├│ ─æß╗Ö lß╗øn vß║Łn tß╗æc cß╗▒c ─æß║Īi l├Ā 5ŽĆ cm/s. Tß╗æc ─æß╗Ö trung b├¼nh cß╗¦a vß║Łt trong mß╗Öt chu k├¼ dao ─æß╗Öng l├Ā
A. 10 cm/s. B. 20 cm/s. C. 0. D. 15 cm/s.
B├Āi 14: Gß╗Źi M l├Ā trung ─æiß╗ām cß╗¦a ─æoß║Īn AB tr├¬n quß╗╣ ─æß║Īo chuyß╗ān ─æß╗Öng cß╗¦a mß╗Öt vß║Łt dao ─æß╗Öng ─æiß╗üu h├▓a. Nß║┐u gia tß╗æc tß║Īi A v├Ā B lß║¦n lŲ░ß╗Żt l├Ā ŌłÆ2 cm/s2 v├Ā 6 cm/s2 th├¼ gia tß╗æc tß║Īi M l├Ā
A. 2 cm/s2. B. 1 cm/s2. C. 4 cm/s2. D. 3 cm/s2.
B├Āi 15: Mß╗Öt vß║Łt dao ─æß╗Öng ─æiß╗üu h├▓a vß╗øi phŲ░ŲĪng tr├¼nh: x = cos(25t) cm (t ─æo bß║▒ng s). V├Āo thß╗Øi ─æiß╗ām t = ŽĆ/100 (s) vß║Łn tß╗æc cß╗¦a vß║Łt l├Ā
A. 25 cm/s. B. 100 cm/s. C. 50 cm/s. D. ŌłÆ100 (cm/s).
---(─Éß╗ā xem ─æß║¦y ─æß╗¦, chi tiß║┐t cß╗¦a t├Āi liß╗ću vui l├▓ng xem tß║Īi online hoß║Ęc ─æ─āng nhß║Łp ─æß╗ā tß║Żi vß╗ü m├Īy)---
─É├üP ├üN PHß║”N LUYß╗åN Tß║¼P
|
1.B |
2.B |
3.A |
4.A |
5.C |
6.A |
7.B |
8.B |
9.D |
10.B |
|
11.A |
12.A |
13.A |
14.A |
15.D |
16.A |
17.C |
18.D |
19.B |
20.C |
|
21.C |
22.C |
23.D |
24.D |
25.D |
26.A |
27.A |
28.C |
29.C |
30.D |
|
31.C |
32.A |
33.A |
34.B |
35.B |
36.D |
37.B |
38.D |
39.B |
40.B |
Tr├¬n ─æ├óy l├Ā mß╗Öt phß║¦n tr├Łch dß║½n nß╗Öi dung C├Īc phŲ░ŲĪng ph├Īp biß╗āu diß╗ģn dao ─æß╗Öng ─æiß╗üu h├▓a v├Ā c├Īc ─æß║Īi lŲ░ß╗Żng ─æß║Ęc trŲ░ng m├┤n Vß║Łt L├Į 12 n─ām 2021-2022. ─Éß╗ā xem to├Ān bß╗Ö nß╗Öi dung c├Īc em ─æ─āng nhß║Łp v├Āo trang hoc247.net ─æß╗ā tß║Żi t├Āi liß╗ću vß╗ü m├Īy t├Łnh.
Hy vß╗Źng t├Āi liß╗ću n├Āy sß║Į gi├║p c├Īc em hß╗Źc sinh ├┤n tß║Łp tß╗æt v├Ā ─æß║Īt th├Ānh t├Łch cao trong hß╗Źc tß║Łp.
T├Āi liß╗ću li├¬n quan
TŲ░ liß╗ću nß╗Ģi bß║Łt tuß║¦n
- Xem thêm