Bài tập 15 trang 158 SBT Toán 9 Tập 1
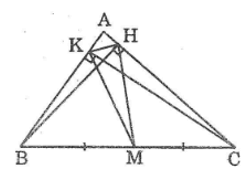
Cho tam giác ABC, các đường cao BH và CK. Chứng minh:
a. Bốn điểm B, C, H, K cùng thuộc một đường tròn
b. HK < BC
Hướng dẫn giải chi tiết
a. Gọi M là trung điểm của BC.
Tam giác BCH vuông tại H có HM là đường trung tuyến nên:
HM = (1/2).BC (tính chất tam giác vuông)
Tam giác BCK vuông tại K có KM là đường trung tuyến nên:
KM = (1/2).BC (tính chất tam giác vuông)
Suy ra: MB = MC = MH = MK
Vậy bốn điểm B, C, H, K cùng nằm trên một đường tròn tâm M bán kính bằng (1/2).BC.
b. Trong đường tròn tâm M ta có KH là dây cung không đi qua tâm, BC là đường kính nên: KH < BC
-- Mod Toán 9 HỌC247
-


Cho đường tròn (O) có hai dây AB, CD không đi qua tâm. Biết rằng khoảng cách từ tâm đến hai dây là bằng nhau. Kết luận nào sau đây là đúng
bởi Ha Ku
 21/01/2021
21/01/2021
A. AB > CD
B. AB = CD
C. AB < CD
D. AB // CD
Theo dõi (0) 1 Trả lời -


Cho đường tròn (O) đường kính AB và dây CD không đi qua tâm. Khẳng định nào sau đây là đúng?
bởi thi trang
 20/01/2021
20/01/2021
A. AB > CD
B. AB = CD
C. AB < CD
D. AB ≤ CD
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có đường cao là BD, CE. Chứng minh rằng B, D, C, E cùng một đường tròn và ED < BC .
bởi hoàng duy
 21/01/2021
21/01/2021
.png) Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 10 trang 104 SGK Toán 9 Tập 1
Bài tập 11 trang 104 SGK Toán 9 Tập 1
Bài tập 16 trang 159 SBT Toán 9 Tập 1
Bài tập 17 trang 159 SBT Toán 9 Tập 1
Bài tập 18 trang 159 SBT Toán 9 Tập 1
Bài tập 19 trang 159 SBT Toán 9 Tập 1
Bài tập 20 trang 159 SBT Toán 9 Tập 1
Bài tập 21 trang 159 SBT Toán 9 Tập 1
Bài tập 22 trang 159 SBT Toán 9 Tập 1
Bài tập 23 trang 159 SBT Toán 9 Tập 1
Bài tập 2.1 trang 159 SBT Toán 9 Tập 1