Bài tập 16 trang 159 SBT Toán 9 Tập 1
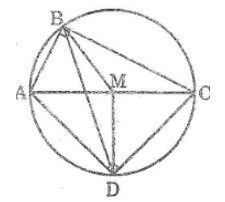
Tứ giác ABCD có \(\widehat B = \widehat D = {90^0}\)
a. Chứng minh rằng bốn điêm A, B, C, D cùng thuộc một đường tròn
b. So sánh độ dài AC và BD. Nếu AC = BD thì tứ giác ABCD là hình gì?
Hướng dẫn giải chi tiết
Tam giác ABC vuông tại B có BM là đường trung tuyến nên:
BM = (1/2).AC (tính chất tam giác vuông)
Tam giác ACD vuông tại D có DM là đường trung tuyến nên:
DM = (1/2).AC (tính chất tam giác vuông)
Suy ra: MA = MB = MC = MD
Vậy bốn điểm A, B, C, D cùng nằm trên một đường tròn tâm M bán kính bằng (1/2).AC.
b. Trong đường tròn tâm M ta có BD là dây cung không đi qua tâm, AC là đường kính nên: BD < AC
AC = BD khi và chỉ khi BD là đường kính. Khi đó tứ giác ABCD là hình chữ nhật.
-- Mod Toán 9 HỌC247
-


Tính bán kính của đường tròn?
bởi Nguyễn Thị Bích
 17/04/2020
17/04/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chuongsminh tứ giác IECB nội tiếp?
bởi Đỗ Xuân Tuyền
 12/04/2020
12/04/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho ∆ABC nhọn nội tiếp đường tròn, hai đường cao BD, CE cắt nhau tại H, tia AO cắt đường tròn tại A'. Chứng minh BHCA' là hình bình hành
bởi Nguyễn Phong
 13/03/2020
13/03/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời
Bài tập SGK khác
Bài tập 11 trang 104 SGK Toán 9 Tập 1
Bài tập 15 trang 158 SBT Toán 9 Tập 1
Bài tập 17 trang 159 SBT Toán 9 Tập 1
Bài tập 18 trang 159 SBT Toán 9 Tập 1
Bài tập 19 trang 159 SBT Toán 9 Tập 1
Bài tập 20 trang 159 SBT Toán 9 Tập 1
Bài tập 21 trang 159 SBT Toán 9 Tập 1
Bài tập 22 trang 159 SBT Toán 9 Tập 1
Bài tập 23 trang 159 SBT Toán 9 Tập 1
Bài tập 2.1 trang 159 SBT Toán 9 Tập 1