HŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo ChŲ░ŲĪng 3 B├Āi 3 H├Ām sß╗æ li├¬n tß╗źc m├┤n To├Īn lß╗øp 11 gi├║p c├Īc em hß╗Źc sinh nß║»m vß╗»ng phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp v├Ā ├┤n luyß╗ćn tß╗æt kiß║┐n thß╗®c.
-
Hoß║Īt ─æß╗Öng khß╗¤i ─æß╗Öng trang 80 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
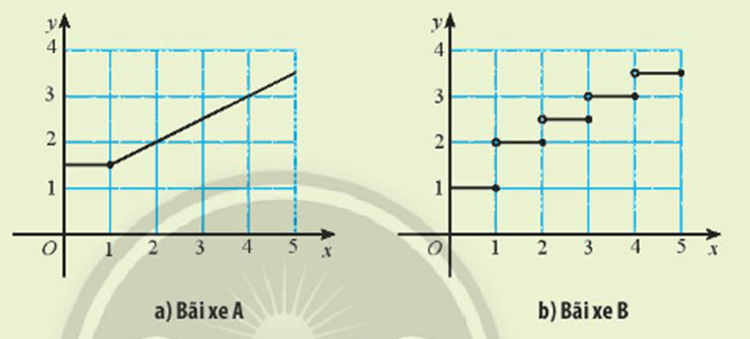
Hai ─æß╗ō thß╗ŗ ß╗¤ hai h├¼nh dŲ░ß╗øi ─æ├óy cho biß║┐t ph├Ł gß╗Łi xe y cß╗¦a ├┤ t├┤ con (t├Łnh theo 10 ngh├¼n ─æß╗ōng) theo thß╗Øi gian gß╗Łi x (t├Łnh theo giß╗Ø) cß╗¦a hai b├Żi xe. C├│ nhß║Łn x├®t g├¼ vß╗ü sß╗▒ thay ─æß╗Ģi cß╗¦a sß╗æ tiß╗ün ph├Ł phß║Żi trß║Ż theo thß╗Øi gian gß╗Łi ß╗¤ mß╗Śi b├Żi ─æß╗Ś xe?
-
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 1 trang 80 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Cho h├Ām sß╗æ \(y = f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}1&{khi\,\,0 \le x \le 1}\\{1 + x}&{khi\,\,1 < x \le 2}\\{5 - x}&{khi\,\,2 < x \le 3}\end{array}} \right.\) c├│ ─æß╗ō thß╗ŗ nhŲ░ H├¼nh 1.
.png)
Tß║Īi mß╗Śi ─æiß╗ām \({x_0} = 1\) v├Ā \({x_0} = 2\), c├│ tß╗ōn tß║Īi giß╗øi hß║Īn \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right)\) kh├┤ng? Nß║┐u c├│, giß╗øi hß║Īn ─æ├│ c├│ bß║▒ng \(f\left( {{x_0}} \right)\) kh├┤ng?
-
Thß╗▒c h├Ānh 1 trang 81 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
X├®t t├Łnh li├¬n tß╗źc cß╗¦a h├Ām sß╗æ:
a) \(f\left( x \right) = 1 - {x^2}\) tß║Īi ─æiß╗ām \({x_0} = 3\);
b) \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{{x^2} + 1}&{khi\,\,x > 1}\\{ - x}&{khi\,\,x \le 1}\end{array}} \right.\) tß║Īi ─æiß╗ām \({x_0} = 1\).
-
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 2 trang 82 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Cho h├Ām sß╗æ \(y = f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{x + 1}&{khi\,\,1 < x \le 2}\\k&{khi\,\,x = 1}\end{array}} \right.\).
a) X├®t t├Łnh li├¬n tß╗źc cß╗¦a h├Ām sß╗æ tß║Īi mß╗Śi ─æiß╗ām \({x_0} \in \left( {1;2} \right)\).
b) T├¼m \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right)\) v├Ā so s├Īnh gi├Ī trß╗ŗ n├Āy vß╗øi \(f\left( 2 \right)\).
c) Vß╗øi gi├Ī trß╗ŗ n├Āo cß╗¦a \(k\) th├¼ \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = k\)?
-
Vß║Łn dß╗źng 1 trang 82 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Tß║Īi mß╗Öt xŲ░ß╗¤ng sß║Żn xuß║źt bß╗Öt ─æ├Ż thß║Īch anh, gi├Ī b├Īn (t├Łnh theo ngh├¼n ─æß╗ōng) cß╗¦a \(x\) (kg) bß╗Öt ─æ├Ż thß║Īch anh ─æŲ░ß╗Żc t├Łnh theo c├┤ng thß╗®c sau:
\(P\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{4,5x}&{khi\,\,0 < x \le 400}\\{4x + k}&{khi\,\,x > 400}\end{array}} \right.\) (\(k\) l├Ā mß╗Öt h├Żng sß╗æ).
a) Vß╗øi \(k = 0\), x├®t t├Łnh li├¬n tß╗źc cß╗¦a h├Ām sß╗æ \(P\left( x \right)\) tr├¬n \(\left( {0; + \infty } \right)\).
b) Vß╗øi gi├Ī trß╗ŗ n├Āo cß╗¦a \(k\) th├¼ h├Ām sß╗æ \(P\left( x \right)\) li├¬n tß╗źc tr├¬n \(\left( {0; + \infty } \right)\)?
-
Thß╗▒c h├Ānh 2 trang 82 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
X├®t t├Łnh li├¬n tß╗źc cß╗¦a h├Ām sß╗æ \(y = \sqrt {x - 1} + \sqrt {2 - x} \) tr├¬n \(\left[ {1;2} \right]\).
-
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 3 trang 82 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Cho hai h├Ām sß╗æ \(y = f\left( x \right) = \frac{1}{{x - 1}}\) v├Ā \(y = g\left( x \right) = \sqrt {4 - x} \).
a) T├¼m tß║Łp x├Īc ─æß╗ŗnh cß╗¦a mß╗Śi h├Ām sß╗æ ─æ├Ż cho.
b) Mß╗Śi h├Ām sß╗æ tr├¬n li├¬n tß╗źc tr├¬n nhß╗»ng khoß║Żng n├Āo? Giß║Żi th├Łch.
-
Thß╗▒c h├Ānh 3 trang 83 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
X├®t t├Łnh li├¬n tß╗źc cß╗¦a h├Ām sß╗æ \(y = \sqrt {{x^2} - 4} \).
-
Thß╗▒c h├Ānh 4 trang 83 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Cho h├Ām sß╗æ \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\frac{{{x^2} - 2x}}{x}}&{khi\,\,x \ne 0}\\a&{khi\,\,x = 0}\end{array}} \right.\).
T├¼m \(a\) ─æß╗ā h├Ām sß╗æ \(y = f\left( x \right)\) li├¬n tß╗źc tr├¬n \(\mathbb{R}\).
-
Vß║Łn dß╗źng 2 trang 83 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Mß╗Öt h├Żng taxi ─æŲ░a ra gi├Ī cŲ░ß╗øc \(T\left( x \right)\) (─æß╗ōng) khi ─æi qu├Żng ─æŲ░ß╗Øng \(x\) (km) cho loß║Īi xe 4 chß╗Ś nhŲ░ sau:
\(T\left( x \right) \)\( = \left\{ {\begin{array}{*{20}{c}}{10000}&{khi\,\,0 < x \le 0,7}\\{ - 10000 + \left( {x - 0,7} \right).14000}&{khi{\rm{ }}0,7 < x \le 20}\\{280200 + \left( {x--20} \right).12000}&{khi{\rm{ }}x > 20}\end{array}} \right.\)
X├®t t├Łnh li├¬n tß╗źc cß╗¦a h├Ām sß╗æ \(T\left( x \right)\).
-
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 4 trang 83 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Cho hai h├Ām sß╗æ \(y = f\left( x \right) = \frac{1}{{x - 1}}\) v├Ā \(y = g\left( x \right) = \sqrt {4 - x} \).
H├Ām sß╗æ \(y = f\left( x \right) + g\left( x \right)\) c├│ li├¬n tß╗źc tß║Īi \(x = 2\) kh├┤ng? Giß║Żi th├Łch.
-
Thß╗▒c h├Ānh 5 trang 84 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
X├®t t├Łnh li├¬n tß╗źc cß╗¦a c├Īc h├Ām sß╗æ:
a) \(y = \sqrt {{x^2} + 1} + 3 - x\);
b) \(y = \frac{{{x^2} - 1}}{x}.\cos x\).
-
Vß║Łn dß╗źng 3 trang 84 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Trong mß║Ęt phß║│ng toß║Ī ─æß╗Ö \(Oxy\), cho ─æŲ░ß╗Øng tr├▓n \(\left( C \right)\) t├óm \(O\), b├Īn k├Łnh bß║▒ng 1. Mß╗Öt ─æŲ░ß╗Øng thß║│ng \(d\) thay ─æß╗Ģi, lu├┤n vu├┤ng g├│c vß╗øi trß╗źc ho├Ānh, cß║»t trß╗źc ho├Ānh tß║Īi ─æiß╗ām \(M\) c├│ ho├Ānh ─æß╗Ö \(x\left( { - 1 < x < 1} \right)\) v├Ā cß║»t ─æŲ░ß╗Øng tr├▓n \(\left( C \right)\) tß║Īi c├Īc ─æiß╗ām \(N\) v├Ā \(P\) (xem H├¼nh 6).
a) Viß║┐t biß╗āu thß╗®c \(S\left( x \right)\) biß╗āu thß╗ŗ diß╗ćn t├Łch cß╗¦a tam gi├Īc \(ONP\).
b) H├Ām sß╗æ \(y = S\left( x \right)\) c├│ li├¬n tß╗źc tr├¬n \(\left( { - 1;1} \right)\) kh├┤ng? Giß║Żi th├Łch.
c) T├¼m c├Īc giß╗øi hß║Īn \(\mathop {\lim }\limits_{x \to {1^ - }} S\left( x \right)\) v├Ā \(\mathop {\lim }\limits_{x \to - {1^ + }} S\left( x \right)\).
-
Giß║Żi B├Āi 1 trang 84 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
X├®t t├Łnh li├¬n tß╗źc cß╗¦a h├Ām sß╗æ:
a) \(f\left( x \right) \)\( = \left\{ {\begin{array}{*{20}{c}}{{x^2} + 1}&{khi\,\,x \ge 0}\\{1 - x}&{khi\,\,x < 0}\end{array}} \right.\) tß║Īi ─æiß╗ām \(x = 0\).
b) \(f\left( x \right) \)\( = \left\{ {\begin{array}{*{20}{c}}{{x^2} + 2}&{khi\,\,x \ge 1}\\x&{khi\,\,x < 1}\end{array}} \right.\) tß║Īi ─æiß╗ām \(x = 1\).
-
Giß║Żi B├Āi 2 trang 84 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Cho h├Ām sß╗æ \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\frac{{{x^2} - 4}}{{x + 2}}}&{khi\,\,x \ne - 2}\\a&{khi\,\,x = - 2}\end{array}} \right.\).
T├¼m \(a\) ─æß╗ā h├Ām sß╗æ \(y = f\left( x \right)\) li├¬n tß╗źc tr├¬n \(\mathbb{R}\).
-
Giß║Żi B├Āi 3 trang 85 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
X├®t t├Łnh li├¬n tß╗źc cß╗¦a c├Īc h├Ām sß╗æ sau:
a) \(f\left( x \right) = \frac{x}{{{x^2} - 4}}\);
b) \(g\left( x \right) = \sqrt {9 - {x^2}} \);
c) \(h\left( x \right) = \cos x + \tan x\).
-
Giß║Żi B├Āi 4 trang 85 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Cho h├Ām sß╗æ \(f\left( x \right) = 2x - \sin x,g\left( x \right) = \sqrt {x - 1} \).
X├®t t├Łnh li├¬n tß╗źc h├Ām sß╗æ \(y = f\left( x \right).g\left( x \right)\) v├Ā \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}}\).
-
Giß║Żi B├Āi 5 trang 85 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Mß╗Öt b├Żi ─æß║Łu xe ├┤ t├┤ ─æŲ░a ra gi├Ī \(C\left( x \right)\) (─æß╗ōng) khi thß╗Øi gian ─æß║Łu xe l├Ā \(x\) (giß╗Ø) nhŲ░ sau:
\(C\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{60000}&{khi\,\,0 < x \le 2}\\{100000}&{khi{\rm{ }}2 < x \le 4}\\{200000}&{khi{\rm{ }}4 < x \le 24}\end{array}} \right.\)
X├®t t├Łnh li├¬n tß╗źc cß╗¦a h├Ām sß╗æ \(C\left( x \right)\).
-
Giß║Żi B├Āi 6 trang 85 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Lß╗▒c hß║źp dß║½n do Tr├Īi ─Éß║źt t├Īc dß╗źng l├¬n mß╗Öt ─æŲĪn vß╗ŗ khß╗æi lŲ░ß╗Żng ß╗¤ khoß║Żng c├Īch \(r\) ß╗¤ tß╗ēnh tß╗½ t├óm cß╗¦a n├│ l├Ā
\(F\left( r \right) = \left\{ {\begin{array}{*{20}{c}}{\frac{{GM{\rm{r}}}}{{{R^3}}}}&{khi\,\,0 < x < R}\\{\frac{{GM}}{{{r^2}}}}&{khi\,\,r \ge R}\end{array}} \right.\)
trong ─æ├│ \(M\) l├Ā khß╗æi lŲ░ß╗Żng, \(R\) l├Ā b├Īn k├Łnh cß╗¦a Tr├Īi ─Éß║źt, \(G\) l├Ā hß║▒ng sß╗æ hß║źp dß║½n.
H├Ām sß╗æ \(F\left( r \right)\) c├│ li├¬n tß╗źc tr├¬n \(\left( {0; + \infty } \right)\) kh├┤ng?
-
B├Āi tß║Łp 1 trang 90 SBT Toa╠ün 11 T├ó╠Żp 1 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
D├╣ng ─æß╗ŗnh ngh─®a, x├®t t├Łnh li├¬n tß╗źc cß╗¦a h├Ām sß╗æ:
a) f(x) = x3 ŌĆÆ 3x + 2 tß║Īi ─æiß╗ām x = ŌĆÆ2;
b) tß║Īi ─æiß╗ām x = 0.
-
B├Āi tß║Łp 2 trang 90 SBT Toa╠ün 11 T├ó╠Żp 1 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
X├®t t├Łnh li├¬n tß╗źc cß╗¦a mß╗Śi h├Ām sß╗æ sau tß║Īi ─æiß╗ām x = 2.
a) f(x) =
b)
-
B├Āi tß║Łp 3 trang 90 SBT Toa╠ün 11 T├ó╠Żp 1 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
X├®t t├Łnh li├¬n tß╗źc cß╗¦a h├Ām sß╗æ:
a) tß║Īi ─æiß╗ām x = ŌĆÆ1;
b) tß║Īi ─æiß╗ām x = 1.
-
B├Āi tß║Łp 4 trang 90 SBT Toa╠ün 11 T├ó╠Żp 1 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
Cho h├Ām sß╗æ . Ti╠Ćm gia╠ü tri╠Ż cu╠ēa tham s├┤╠ü a ─æ├¬╠ē ha╠Ćm s├┤╠ü y = f(x) li├¬n tu╠Żc ta╠Żi x = 2?
-
B├Āi tß║Łp 5 trang 90 SBT Toa╠ün 11 T├ó╠Żp 1 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
X├®t t├Łnh li├¬n tß╗źc cß╗¦a c├Īc h├Ām sß╗æ sau:
a) f(x) = x3 ŌĆÆ x2 + 2;
b)
c)
d) .
-
B├Āi tß║Łp 6 trang 90 SBT Toa╠ün 11 T├ó╠Żp 1 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
X├®t t├Łnh li├¬n tß╗źc cß╗¦a c├Īc h├Ām sß╗æ sau:
a)
b) .
-
B├Āi tß║Łp 7 trang 90 SBT Toa╠ün 11 T├ó╠Żp 1 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
Cho hai h├Ām sß╗æ f(x) = x ŌĆÆ 1 v├Ā g(x) = x2 ŌĆÆ 3x + 2. X├®t t├Łnh li├¬n tß╗źc cß╗¦a c├Īc h├Ām sß╗æ:
a) y = f(x).g(x);
b)
c)
-
B├Āi tß║Łp 8 trang 91 SBT Toa╠ün 11 T├ó╠Żp 1 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
Cho hai h├Ām sß╗æ v├Ā .
T├¼m gi├Ī trß╗ŗ cß╗¦a tham sß╗æ a sao cho h├Ām sß╗æ h(x) = f(x) + g(x) li├¬n tß╗źc tß║Īi x = 1?
-
B├Āi tß║Łp 9 trang 91 SBT Toa╠ün 11 T├ó╠Żp 1 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
Cho h├Ām sß╗æ y = f(x) =
T├¼m gi├Ī trß╗ŗ cß╗¦a c├Īc tham sß╗æ a v├Ā b sao cho h├Ām sß╗æ y = f(x) li├¬n tß╗źc tr├¬n ŌäØ?
-
B├Āi tß║Łp 10 trang 91 SBT Toa╠ün 11 T├ó╠Żp 1 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
Chß╗®ng minh rß║▒ng phŲ░ŲĪng tr├¼nh:
a) x3 + 2x ŌĆÆ 1 = 0 c├│ nghiß╗ćm thuß╗Öc khoß║Żng (ŌĆÆ1; 1).
b) c├│ nghiß╗ćm thuß╗Öc khoß║Żng (0; 1).
-
B├Āi tß║Łp 11 trang 91 SBT Toa╠ün 11 T├ó╠Żp 1 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
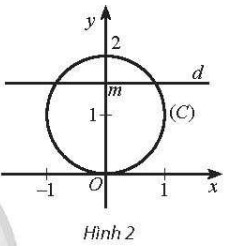
Trong mß║Ęt phß║│ng tß╗Źa ─æß╗Ö Oxy, cho ─æŲ░ß╗Øng tr├▓n (C): x2 + (y ŌĆÆ 1)2 = 1. Vß╗øi mß╗Śi sß╗æ thß╗▒c m, gß╗Źi Q(m) l├Ā sß╗æ giao ─æiß╗ām cß╗¦a ─æŲ░ß╗Øng thß║│ng d: y = m vß╗øi ─æŲ░ß╗Øng tr├▓n (C). Viß║┐t c├┤ng thß╗®c x├Īc ─æß╗ŗnh h├Ām sß╗æ y = Q(m). H├Ām sß╗æ n├Āy kh├┤ng li├¬n tß╗źc tß║Īi c├Īc ─æiß╗ām n├Āo?
-
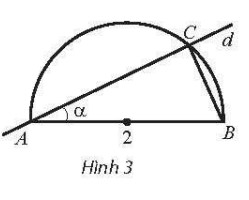
B├Āi tß║Łp 12 trang 91 SBT Toa╠ün 11 T├ó╠Żp 1 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
Cho nß╗Ła ─æŲ░ß╗Øng tr├▓n ─æŲ░ß╗Øng k├Łnh AB = 2. ─ÉŲ░ß╗Øng thß║│ng d thay ─æß╗Ģi lu├┤n ─æi qua A, cß║»t nß╗Ła ─æŲ░ß╗Øng tr├▓n tß║Īi C v├Ā tß║Īo vß╗øi ─æŲ░ß╗Øng thß║│ng AB g├│c .
K├Ł hiß╗ću diß╗ćn t├Łch tam gi├Īc ABC l├Ā S(╬▒) (phß╗ź thuß╗Öc v├Āo ╬▒). X├®t t├Łnh li├¬n tß╗źc cß╗¦a h├Ām sß╗æ S(╬▒) tr├¬n khoß║Żng v├Ā t├Łnh c├Īc giß╗øi hß║Īn