KG Toán NC THCS và Luyện thi 10 Chuyên
Giải bài 2 tr 63 sách GK Toán Hình lớp 11
Cho tứ diện ABCD. Trên cạnh AB lấy một điểm M. Cho \((\alpha )\) là mặt phẳng qua M, song song với hai đường thẳng AC và BD
a) Tìm giao tuyến của \((\alpha )\) với các mặt tứ diện
b) Thiết diện của tứ diện cắt bởi mặt phẳng \((\alpha )\) là hình gì?
Hướng dẫn giải chi tiết bài 2
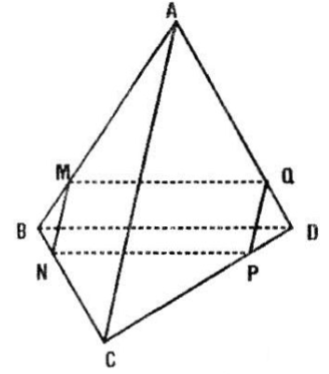
Câu a:
Ta có:
\((\alpha ) //AC\) và \(AC\subset (ABC)\)
⇒ AC song song với giao tuyến của \((\alpha )\) và (ABC)
* Trên mp(ABC) kẻ MN // AC \((N\in BC)\)
\(\Rightarrow MN=(\alpha )\cap (ABC)\)
\((\alpha ) // BD\) và \(BD\subset (ABC)\)
⇒ BD song song với giao tuyến của \((\alpha )\) và (BCD)
* Trên mp(BCD) kẻ \(NP // BD (P\in CD)\)
\(\Rightarrow NP=(\alpha )\cap (BCD)\)
\((\alpha ) //AC\) và \(AC\subset (ACD)\)
⇒ AC song song với giao tuyến của \((\alpha )\) và (ACD)
* Trên mp(ACD) kẻ PQ // AC \((Q\in AD)\)
\(\Rightarrow PQ=(\alpha )\cap (ACD)\)
Ta thấy M và Q là 2 điểm chung của mp\((\alpha )\) và (ABD)
\(\Rightarrow (\alpha )\cap (ABD)=MQ\)
Câu b:
Theo câu a) ta có:
\(\left.\begin{matrix} MN //AC\\ PQ //AC \end{matrix}\right\}\Rightarrow MN // PQ\)
và \((\alpha ) // BD, BD\subset (ABD)\Rightarrow BD // MQ\)
Mặt khác NP // AC ⇒ NP // MQ (2)
Từ (1) và (2) ⇒ MNPQ là hình bình hành
⇒ Thiết diện cảu tứ diện cắt bởi mp\((\alpha )\) là hình bình hành.
-- Mod Toán 11 HỌC247
Để luyện tập thêm dạng bài tương tự như Bài tập 2 trang 63 trong SGK các em làm thêm câu hỏi trắc nghiệm sau để cũng cố kỹ năng làm dạng bài.
-
Câu 1:
Cho tứ diện ABCD. Giả sử M thuộc đoạn BC. Một mặt (∝) qua M song song với AB và CD. Thiết diện của (∝) và hình tứ diện ABCD là hình gì?
- A. Hình thang có đúng một cặp cạnh song song
- B. Hình bình hành
- C. Tam giác
- D. Ngũ giác
.PNG)
-
Xác định các góc trong hình vẽ
bởi Lê Tấn Vũ
10/10/2018
Qua điểm O, vẽ năm đường thẳng phân biệt.
a) Có bao nhiêu góc trong hình vẽ?
b) Trong các góc ấy,có bao nhiêu cặp góc đối đỉnh nhỏ hơn góc bẹt?
c) Xét các góc không có điểm chung, chứng tỏ tồn tại một góc lớn hơn hoặc bằng 360 , tồn tại một góc nhỏ hơn hoặc bằng 360.
Theo dõi (0) 1 Trả lời -
Chứng minh tia Ox' là tia phân giác của góc A'OB'
bởi Tieu Dong
10/10/2018
Cho hai góc đối đỉnh AOB và A'OB'. Gọi Ox là tia phân giác của góc AOB,Ox' là tia đối của tia Ox. Vì sao Ox' là tia phân giác của góc A'OB'?
Theo dõi (0) 1 Trả lời -
hình không gian. 11
bởi Tam Thiên
08/08/2017
Cho hình chop' SABCD . ABCD là hình bình hành . M,N lần lượt là trung điểm của SB và SD .(AMN) \(\cap\) SC=P a,Tính SP/PC
b,Thay M ở SB t/m~ SM/MB=2 . Tính SP/PC
c,Thay M ở SB t/m SM/MB=2/5 Tính SP/PC
Theo dõi (1) 2 Trả lời -
hình không gian. 11
bởi Tam Thiên
08/08/2017
Hình lăng trụ ABC A'B'C' . G là trọng tâm của tam giác ABC . G' là trọng tâm của tam giác A'B'C' . O=AB'\(\cap\) A'B . Mệnh đề nào đúng ,sai. Vì sao ?
1, GG'//(ABB'A')
2,GG'//(OAA')
3,GG'//BB'
4,(GG'A)//(BB'O)
5,AA'//(GG'O)
6,OA//GB
7,OB cắt AB'
8,GO và AC chéo nhau
Theo dõi (1) 1 Trả lời
Được đề xuất cho bạn
