Giải bài 2.20 tr 71 SBT Hình học 11
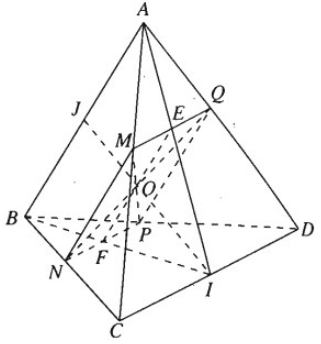
Cho tứ diện ABCD. Qua điểm M nằm trên AC ta dựng một mặt phẳng (α) song song với AB và CD. Mặt phẳng này lần lượt cắt các cạnh BC, BD và AD tại N, P và Q.
a) Tứ giác MNPQ là hình gì?
b) Gọi O là giao điểm hai đường chéqo của tứ giác MNPQ. Tìm tập hợp các điểm O khi M di động trên đoạn AC.
Hướng dẫn giải chi tiết
a) \(\left\{ \begin{array}{l}
\left( \alpha \right)\parallel AB\\
AB \subset \left( {ABC} \right)
\end{array} \right.\) ⇒ (α) ∩ (ABC) = MN và MN // AB
Ta có N ∈ (BCD) và \(\left\{ \begin{array}{l}
\left( \alpha \right)\parallel CD\\
CD \subset \left( {BCD} \right)
\end{array} \right.\)
Suy ra (α) ∩ (BCD) = NP và NP // CD
Ta có P ∈ (ABD) và \(\left\{ \begin{array}{l}
\left( \alpha \right)\parallel AB\\
AB \subset \left( {ABD} \right)
\end{array} \right.\) nên (α) ∩ (ABD) = PQ và PQ // AB và (α) ∩ (ACD) = MQ; MQ // CD
Do đó MN // PQ và NP // MQ, Vậy tứ giác MNPQ là hình bình hành.
b) Ta có: MP ∩ NQ = O. Gọi I là trung điểm của CD.
Trong tam giác ACD có : MQ // CD ⇒ AI cắt MQ tại trung điểm E của MQ.
Trong tam giác ACD có : NP // CD ⇒ BI cắt NP tại trung điểm F của NP.
Vì MNPQ là hình bình hành nên ta có \(\left\{ \begin{array}{l}
Q \in \left( {ACD} \right)\\
\left( \alpha \right)\parallel CD
\end{array} \right.\)
EF // MN ⇒ EF // AB
Trong ΔABI ta có EF // AB suy ra : IO cắt AB tại trung điểm J
⇒ I, O, J thẳng hàng
⇒ O ∈ IJ cố định.
Vì M di động trên đoạn AC nên O chạy trong đoạn IJ . Vậy tập hợp các điểm O là đoạn IJ.
-- Mod Toán 11 HỌC247
-


Cho tứ diện đều ABCD cạnh a. I, J lần lượt là trung điểm của AC và BC. Gọi K là giao điểm trên cạnh BD với KB = 2KD. Thiết diện của tứ diện với mặt phẳng (IJK) là hình gì?
bởi minh thuận
 22/01/2021
22/01/2021
A. thiết diện là hình thang cân.
B. hình bình hành.
C. tam giác.
D. tứ giác không có cặp cạnh nào song song.
Theo dõi (0) 1 Trả lời -


Cho tứ diện ABCD. Giả sử M thuộc đoạn BC. Một mặt (∝) qua M song song với AB và CD. Thiết diện của (∝) và hình tứ diện ABCD là hình gì?
bởi Spider man
 22/01/2021
22/01/2021
A. Hình thang có đúng một cặp cạnh song song
B. Hình bình hành
C. Hình tam giác
D. Hình ngũ giác
Theo dõi (0) 1 Trả lời -


Cho tứ diện ABCD, điểm M thuộc AC. Mặt phẳng (∝) đi qua M, song song với AB và AD. Thiết diện (∝) với tứ diện ABCD là hình gì?
bởi nguyen bao anh
 21/01/2021
21/01/2021
A. Thiết diện là tam giác
B. Hình bình hành
C. Hình thoi
D. Hình thang
Theo dõi (0) 1 Trả lời -


A. a // b và b ∩ (∝) = ∅
B. a // b và b // (∝)
C. a // b và b ⊂ (∝)
D. a ∩ (∝) = ∅
Theo dõi (0) 1 Trả lời -


Giải phương trình: \(2a^2 - 3ab - b^2 = 0\)?
bởi Tạ Anh Khang
 04/08/2020
04/08/2020
Giải phương trình: 2a^2 - 3ab - b^2 = 0. Không dùng cách tìm nghiệm qua đenta và cách đặt nhân tử chung thì còn cách làm nào nhanh hơn, khác ko vậy
Theo dõi (1) 1 Trả lời
Bài tập SGK khác
Bài tập 2.18 trang 71 SBT Hình học 11
Bài tập 2.19 trang 71 SBT Hình học 11
Bài tập 2.21 trang 72 SBT Hình học 11
Bài tập 23 trang 59 SGK Hình học 11 NC
Bài tập 24 trang 59 SGK Hình học 11 NC
Bài tập 25 trang 59 SGK Hình học 11 NC
Bài tập 26 trang 59 SGK Hình học 11 NC