Giải bài 2.18 tr 71 SBT Hình học 11
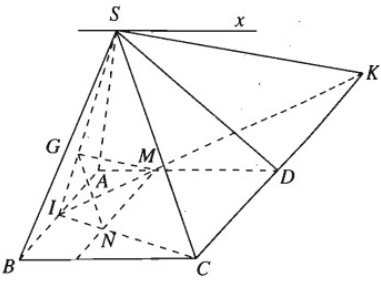
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi G là trọng tâm của tam giác SAB và I là trung điểm của AB. Lấy điểm M trong đoạn AD sao cho AD = 3AM.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
b) Đường thẳng qua M song song với AB cắt CI tại N. Chứng minh rằng NG // (SCD).
c) Chứng minh rằng MG // (SCD).
Hướng dẫn giải chi tiết
a) Dễ thấy S là một điểm chung của hai mặt phẳng (SAD) và (SBC).
Ta có:
\(\left\{ \begin{array}{l}
AD \subset \left( {SAD} \right)\\
BC \subset \left( {SBC} \right)\\
AD\parallel BC
\end{array} \right.\) ⇒ (SAD) ∩ (SBC) = Sx và Sx // AD // BC.
b) Ta có: MN // IA // CD \( \Rightarrow \frac{{AM}}{{AD}} = \frac{{IN}}{{IC}} = \frac{1}{3}\)
Mà \(\frac{{IG}}{{IS}} = \frac{1}{3}\) (G là trọng tâm của ∆SAB) nên \(\frac{{IG}}{{IS}} = \frac{{IN}}{{IC}} = \frac{1}{3}\) ⇒ GN // SC
SC ⊂ (SCD) ⇒ GN // (SCD)
c) Giả sử IM cắt CD tại K ⇒ SK ⊂ (SCD)
MN // CD ⇒ \(MN\parallel CD \Rightarrow \frac{{MN}}{{CK}} = \frac{{IN}}{{IC}} = \frac{1}{3} \Rightarrow \frac{{IM}}{{IK}} = \frac{1}{3}\)
Ta có: \(\left\{ \begin{array}{l}
\frac{{IG}}{{IS}} = \frac{1}{3}\\
\frac{{IM}}{{IK}} = \frac{1}{3}
\end{array} \right. \Rightarrow GM\parallel SK \Rightarrow GM\parallel \left( {SCD} \right)\)
-- Mod Toán 11 HỌC247
-


Cho tứ diện ABCD. M, N lần lượt là trọng tâm của các tam giác ABC, ABD. Thiết diện của tứ diện với mặt phẳng (∝) chứa MN và song song với AB là hình gì?
bởi Lê Tường Vy
 22/01/2021
22/01/2021
A. tam giác
B. hình bình hành
C. hình thoi
D. hình thang có đúng một cặp cạnh song song
Theo dõi (0) 1 Trả lời -


Cho hình chóp S.ABCD có đáy ABCD là một hình bình hành. Một mặt phẳng (P) đồng thời song song với AC và SB lần lượt cắt các đoạn thẳng SA, AB, BC, SC, SD và BD tại M, N, E, F, I, J. khi đó ta có.
bởi Nguyễn Ngọc Sơn
 22/01/2021
22/01/2021
A. MN // (SCD)
B. EF // (SAD)
C. NF // (SAD)
D. IJ // (SAB)
Theo dõi (0) 1 Trả lời -


Cho tứ diện ABCD. Hai điểm M, N lần lượt là trung điểm của AC, AD. Mặt phẳng (∝) chứa MN và song song với AB. Thiết diện của (∝) với tứ diện ABCD là:
bởi Nhat nheo
 22/01/2021
22/01/2021
A. hình thang
B. hình bình hành
C. hình chữ nhật
D. hình vuông
Theo dõi (0) 1 Trả lời -


Cho hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng, có tâm lần lượt là O và O’. Chọn khẳng định đúng trong các khẳng định sau:
bởi Hy Vũ
 22/01/2021
22/01/2021
A. OO’ // (ABCD)
B. OO’ // (ABEF)
C. OO’ // (BDF)
D. OO’ / /(ADF)
Theo dõi (0) 1 Trả lời -


Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Gọi M là trung điểm của SA. Thiết diện của mặt phẳng (MCD) với hình chóp S.ABCD là hình gì?
bởi Hong Van
 22/01/2021
22/01/2021
A. tam giác
B. hình bình hành
C. hình thang
D. hình thoi
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 2.16 trang 71 SBT Hình học 11
Bài tập 2.17 trang 71 SBT Hình học 11
Bài tập 2.19 trang 71 SBT Hình học 11
Bài tập 2.20 trang 71 SBT Hình học 11
Bài tập 2.21 trang 72 SBT Hình học 11
Bài tập 23 trang 59 SGK Hình học 11 NC
Bài tập 24 trang 59 SGK Hình học 11 NC
Bài tập 25 trang 59 SGK Hình học 11 NC
Bài tập 26 trang 59 SGK Hình học 11 NC