Giải bài 2.21 tr 72 SBT Hình học 11
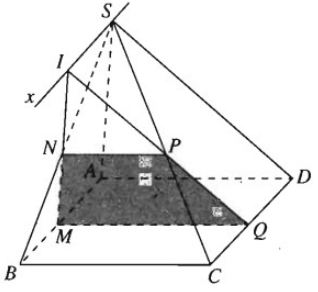
ho hình chóp S.ABCD có đáy là hình bình hành ABCD. M là một điểm di động trên đoạn AB. Một mặt phẳng (α) đi qua M và song song với SA và BC; (α) cắt SB, SC và CD lần lượt tại N, P và Q
a) Tứ giác MNPQ là hình gì?
b) Gọi I là giao điểm của MN và PQ. Chứng minh rằng I nằm trên một đường thẳng cố định.
Hướng dẫn giải chi tiết
a) Vì M ∈ (SAB) và \(\left\{ \begin{array}{l}
\left( \alpha \right)\parallel SA\\
SA \subset \left( {SAB} \right)
\end{array} \right.\) nên (α) ∩ (SAB) = MN và MN // SA
Vì N ∈ (SBC) và \(\left\{ \begin{array}{l}
\left( \alpha \right)\parallel BC\\
BC \subset \left( {SBC} \right)
\end{array} \right.\) nên (α) ∩ (SBC) = NP và NP // BC (1)
Ta có \(\left\{ \begin{array}{l}
P,Q \in \left( \alpha \right)\\
P,Q \in \left( {SCD} \right)
\end{array} \right.\) ⇒ (α) ∩ (SCD) = PQ
Q ∈ CD ⇒ Q ∈ (ABCD) và \(\left\{ \begin{array}{l}
\left( \alpha \right)\parallel BC\\
BC \subset \left( {ABCD} \right)
\end{array} \right.\) nên (α) ∩ (ABCD) = QM và QM // BC (2)
Từ (1) và (2) suy ra tứ giác MNPQ là hình thang.
b) Ta có:
\(\left\{ \begin{array}{l}
S \in \left( {SAB} \right) \cap \left( {SCD} \right)\\
AB \subset \left( {SAB} \right),CD \subset \left( {SCD} \right)\\
AB\parallel CD
\end{array} \right.\) ⇒ (SAB) ∩ (SCD) = Sx và Sx // AB // CD
MN ∩ PQ = I ⇒ \(\left\{ \begin{array}{l}
I \in MN\\
I \in PQ
\end{array} \right.\)
MN ⊂ (SAB) ⇒ I ∈ (SAB), PQ ⊂ (SCD) ⇒ I ∈ (SCD)
⇒ I ∈ (SAB) ∩ (SCD) ⇒ I ∈ Sx
(SAB) và (SCD) cố định ⇒ Sx cố định ⇒ I thuộc Sx cố định.
-- Mod Toán 11 HỌC247
-

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chứng minh SB vuông góc với (ABCD)?
bởi Tho Thieu
 15/04/2020
15/04/2020
Câu III
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chứng minh BC ⊥ SB?
bởi Nguyễn Thành
 09/04/2020
09/04/2020
Cho hình chóp SABC. SA vuông góc với đáy (ABC) và đáy là tam giác vuông tại B
a/ CM BC ⊥ SB
b/ từ A lần lượt kẻ hai đường cao AH, AK trong tam giác SAB và SAC, CMR:AH ⊥(SBC), SC ⊥(AHK)
Theo dõi (0) 1 Trả lời -


Cho hình chóp S.ABCD có đáy là hình thoi và SA=SB=SC=SD, O là giao điểm của AC và BD. Chứng minh rằng SO vuông góc với (ABCD).
bởi Phuc Nguyen
 31/03/2020
31/03/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chứng minh BC vuông góc mp(AID) biết tứ diện ABCD có các tam giác ABC, DBC cân
bởi Diệu Linh
 15/02/2020
15/02/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời