Bài tập 25 trang 59 SGK Hình học 11 NC
Cho hình tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB và AC
a. Xét vị trí tương đối của đường thẳng MN và mp(BCD)
b. Gọi d là giao tuyến của hai mặt phẳng (DMN) và (DBC). Xét vị trí tương đối của d và mp(ABC)
Hướng dẫn giải chi tiết
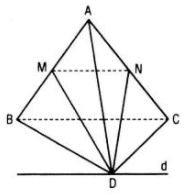
a) MN là đường trung bình của tam giác ABC nên MN // BC
Suy ra: MN // mp(BCD) (vì MN ⊄ (BCD))
b) Vì MN // (BCD) nên mp(DMN) đi qua MN cắt mp(BCD) theo giao tuyến d // MN.
Do đó d // mp(ABC)
-- Mod Toán 11 HỌC247
-


Tìm các giao điểm của CD và AD với (MNK)
bởi Tịch Kiệt
 02/10/2019
02/10/2019
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Xác định thiết diện của hình chóp khi cắt bởi anpha biết hình chóp S.ABCD có đáy ABCD là hình thang
bởi Chu Dũng
 07/08/2019
07/08/2019
Câu 2: Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB đáy lớn). Trên cạnh BC lấy điểm M. Gọi anpha là mặt phẳng đi qua điểm M, song song với AB và SC
a) xác định thiết diện của hình chóp khi cắt bởi anpha
b) CMR giao tuyến của anpha và (SAD) song song với SD
Câu 3: Cho hình chóp S.ABCD có đáy là hình bình hành. Xác định thiết diện của hình chóp S.ABCD khi cắt bởi măt phẳng anpha, biết anpha đi qua trung điểm M của AB và song song với SA, BD
Theo dõi (0) 1 Trả lời -


Xác định thiết diện của hình chóp khi cắt bởi mp đi qua trung điểm M của cạnh AB
bởi Lê Minh Trí
 10/10/2018
10/10/2018
cho hình chóp S.ABCD có đáy là 1 hình bình hành . xác định thiết diện của hình chóp khi cắt bởi mặt phẳng đi qua trung điểm M của cạnh AB , song song với BD và SA
Theo dõi (0) 1 Trả lời -


Bài 2.20 trang 74 sách bài tập Hình học 11
bởi Phan Thị Trinh
 10/10/2018
Bài 2.20 (Sách bài tập - trang 74)
10/10/2018
Bài 2.20 (Sách bài tập - trang 74)Cho tứ diện ABCD. Qua điểm M nằm trên AC ta dựng một mặt phẳng \(\left(\alpha\right)\) song song với AB và CD. Mặt phẳng này lần lượt cắt các cạnh BC, BD và AD tại N, P, Q
a) Tứ giác MNPQ là hình gì ?
b) Gọi O là giao điểm hai đường chéo của tứ giác MNPQ. Tìm tập hợp các điểm O khi M di động trên đoạn AC ?
Theo dõi (0) 1 Trả lời -


Bài 2.19 trang 74 sách bài tập Hình học 11
bởi Lê Nguyễn Hạ Anh
 10/10/2018
Bài 2.19 (Sách bài tập - trang 74)
10/10/2018
Bài 2.19 (Sách bài tập - trang 74)Cho hình chóp S.ABCD có đáy là hình thang ABCD, đáy lớn là AD và AD = 2BC. Gọi O là giao điểm của AC và BD, G là trọng tâm của tam giác SCD
a) Chứng minh rằng OG // (SBC)
b) Cho M là trung điểm của SD. Chứng minh rằng CM // (SAB)
c) Giả sử điểm I nằm trong đoạn SC sao cho \(SC=\dfrac{3}{2}SI\). Chứng minh rằng SA // (BID)
Theo dõi (0) 1 Trả lời





