Nhß║▒m hß╗ć thß╗æng kiß║┐n thß╗®c chŲ░ŲĪng tr├¼nh To├Īn 11 Kß║┐t nß╗æi tri thß╗®c, Hoc247 ─æ├Ż t├│m tß║»t l├Į thuyß║┐t B├Āi H├Ām sß╗æ lŲ░ß╗Żng gi├Īc v├Ā b├Āi tß║Łp tham khß║Żo b├¬n dŲ░ß╗øi ─æ├óy. Mß╗Øi c├Īc em tham khß║Żo v├Ā ─æß║Ęt c├óu hß╗Åi c├Īc b├Āi tß║Łp li├¬n quan ─æß╗ā cß╗Öng ─æß╗ōng Hoc247 sß║Į sß╗øm giß║Żi ─æ├Īp cho c├Īc em.
1.1. ─Éß╗ŗnh ngh─®a h├Ām sß╗æ lŲ░ß╗Żng gi├Īc
1.2. H├Ām sß╗æ chß║Ąn, h├Ām sß╗æ lß║╗, h├Ām sß╗æ tuß║¦n ho├Ān
1.3. ─Éß╗ō thß╗ŗ v├Ā t├Łnh chß║źt cß╗¦a h├Ām sß╗æ y = sin x
1.4. ─Éß╗ō thß╗ŗ v├Ā t├Łnh chß║źt cß╗¦a h├Ām sß╗æ y = cos x
1.5. ─Éß╗ō thß╗ŗ v├Ā t├Łnh chß║źt cß╗¦a h├Ām sß╗æ y = tan x
T├│m tß║»t l├Į thuyß║┐t
1.1. ─Éß╗ŗnh ngh─®a h├Ām sß╗æ lŲ░ß╗Żng gi├Īc
|
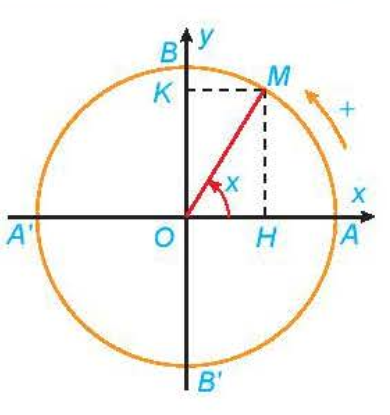
- Quy tß║»c ─æß║Ęt tŲ░ŲĪng ß╗®ng mß╗Śi sß╗æ thß╗▒c x vß╗øi sß╗æ thß╗▒c sinx ─æŲ░ß╗Żc gß╗Źi l├Ā h├Ām sß╗æ sin, k├Ł hiß╗ću l├Ā y = sinx. Tß║Łp x├Īc ─æß╗ŗnh cß╗¦a h├Ām sß╗æ sin l├Ā \(\mathbb{R}\). - Quy tß║»c ─æß║Ęt tŲ░ŲĪng ß╗®ng mß╗Śi sß╗æ thß╗▒c x vß╗øi sß╗æ thß╗▒c cosx ─æŲ░ß╗Żc gß╗Źi l├Ā h├Ām sß╗æ c├┤sin, k├Ł hiß╗ću l├Ā y = cosx. Tß║Łp x├Īc ─æß╗ŗnh cß╗¦a h├Ām sß╗æ c├┤, sin l├Ā \(\mathbb{R}\). - H├Ām sß╗æ tang l├Ā h├Ām sß╗æ ─æŲ░ß╗Żc cho bß║▒ng c├┤ng thß╗®c \(y = {\sin x \over \cos x}\), k├Ł hiß╗ću l├Ā y= tanx. Tß║Łp x├Īc ─æß╗ŗnh cß╗¦a h├Ām sß╗æ tang l├Ā \(\mathbb{R} \backslash\{{\pi \over 2}+k\pi|k\in \mathbb{Z} \}\).
- H├Ām sß╗æ c├┤tang l├Ā h├Ām sß╗æ ─æŲ░ß╗Żc cho bß║▒ng c├┤ng thß╗®c \(y = { \cos x\over \sin x}\), k├Ł hiß╗ću l├Ā y= cotx. Tß║Łp x├Īc ─æß╗ŗnh cß╗¦a h├Ām sß╗æ cotang l├Ā \(\mathbb{R} \backslash\{k\pi| k\in \mathbb{Z}\}\).
|
1.2. H├Ām sß╗æ chß║Ąn, h├Ām sß╗æ lß║╗, h├Ām sß╗æ tuß║¦n ho├Ān
a) H├Ām sß╗æ chß║Ąn, h├Ām sß╗æ lß║╗
|
Cho h├Ām sß╗æ y = f(x) c├│ tß║Łp x├Īc ─æß╗ŗnh l├Ā D. - H├Ām sß╗æ f(x) ─æŲ░ß╗Żc gß╗Źi l├Ā h├Ām sß╗æ chß║Ąn nß║┐u \(\forall x \in D\) th├¼ \(ŌłÆ x \in D\) v├Ā f(-x)=f(x). ─Éß╗ō thß╗ŗ cß╗¦a mß╗Öt h├Ām sß╗æ chß║Ąn nhß║Łn trß╗źc tung l├Ā trß╗źc ─æß╗æi xß╗®ng. - H├Ām sß╗æ f(x) ─æŲ░ß╗Żc gß╗Źi l├Ā h├Ām sß╗æ lß║╗ nß║┐u \(\forall x \in D\) th├¼ \(ŌłÆ x \in D\) v├Ā f(-x)=-f(x). ─Éß╗ō thß╗ŗ cß╗¦a mß╗Öt h├Ām sß╗æ lß║╗ nhß║Łn gß╗æc toß║Ī ─æß╗Ö l├Ā t├óm ─æß╗æi xß╗®ng. |
Nhß║Łn x├®t. ─Éß╗ā vß║Į ─æß╗ō thß╗ŗ cß╗¦a mß╗Öt h├Ām sß╗æ chß║Ąn (tŲ░ŲĪng ß╗®ng, lß║╗), ta chß╗ē cß║¦n vß║Į phß║¦n ─æß╗ō thß╗ŗ cß╗¦a h├Ām sß╗æ vß╗øi nhß╗»ng x dŲ░ŲĪng, sau ─æ├│ lß║źy ─æß╗æi xß╗®ng phß║¦n ─æß╗ō thß╗ŗ ─æ├Ż vß║Į qua trß╗źc tung (tŲ░ŲĪng ß╗®ng, qua gß╗æc toß║Ī ─æß╗Ö), ta sß║Į ─æŲ░ß╗Żc ─æß╗ō thß╗ŗ cß╗¦a h├Ām sß╗æ ─æ├Ż cho.
b) H├Ām sß╗æ tuß║¦n ho├Ān
|
H├Ām sß╗æ y = f(x) c├│ tß║Łp x├Īc ─æß╗ŗnh D ─æŲ░ß╗Żc gß╗Źi l├Ā h├Ām sß╗æ tuß║¦n ho├Ān nß║┐u tß╗ōn tß║Īi sß╗æ T kh├Īc 0 sao cho vß╗øi mß╗Źi x \(\in\) D ta c├│: i) \(x+ T \in D\) v├Ā \(xŌłÆ T \in D\) ii) f(x+T)= f(x). Sß╗æ T dŲ░ŲĪng nhß╗Å nhß║źt thoß║Ż m├Żn c├Īc ─æiß╗üu kiß╗ćn tr├¬n (nß║┐u c├│) ─æŲ░ß╗Żc gß╗Źi l├Ā chu k├¼ cß╗¦a h├Ām sß╗æ tuß║¦n ho├Ān ─æ├│. |
Nhß║Łn x├®t
- C├Īc h├Ām sß╗æ y = sinx v├Ā y = cosx tuß║¦n ho├Ān vß╗øi chu k├¼ \(2\pi\). C├Īc h├Ām sß╗æ y = tanx v├Ā y = cotx tuß║¦n ho├Ān vß╗øi chu k├¼ \(\pi\).
- ─Éß╗ā vß║Į ─æß╗ō thß╗ŗ cß╗¦a mß╗Öt h├Ām sß╗æ tuß║¦n ho├Ān vß╗øi chu k├¼ T, ta chß╗ē cß║¦n vß║Į ─æß╗ō thß╗ŗ cß╗¦a h├Ām sß╗æ n├Āy tr├¬n ─æoß║Īn [a; a + T], sau ─æ├│ dß╗ŗch chuyß╗ün song song vß╗øi trß╗źc ho├Ānh phß║¦n ─æß╗ō thß╗ŗ ─æ├Ż vß║Į sang phß║Żi v├Ā sang tr├Īi c├Īc ─æoß║Īn c├│ ─æß╗Ö d├Āi lß║¦n lŲ░ß╗Żt l├Ā T, 2T, 3T, ... ta ─æŲ░ß╗Żc to├Ān bß╗Ö ─æß╗ō thß╗ŗ cß╗¦a h├Ām sß╗æ.
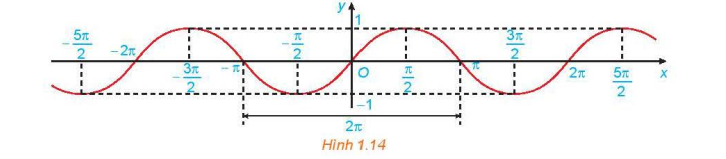
1.3. ─Éß╗ō thß╗ŗ v├Ā t├Łnh chß║źt cß╗¦a h├Ām sß╗æ y = sin x
|
H├Ām sß╗æ y = sin x: - C├│ tß║Łp x├Īc ─æß╗ŗnh l├Ā R v├Ā tß║Łp gi├Ī trß╗ŗ l├Ā [-1; 1]. - L├Ā h├Ām sß╗æ lß║╗ v├Ā tuß║¦n ho├Ān vß╗øi chu k├¼ \(2\pi\). - ─Éß╗ōng biß║┐n tr├¬n mß╗Śi khoß║Żng \(\left(-{\pi \over 2}+k2\pi;{\pi \over 2}+k2\pi\right)\), v├Ā nghß╗ŗch biß║┐n tr├¬n mß╗Śi khoß║Żng \(\left({\pi \over 2}+k2\pi;{3\pi \over 2}+k2\pi\right), k\in \mathbb{Z}\). - C├│ ─æß╗ō thß╗ŗ ─æß╗æi xß╗®ng qua gß╗æc toß║Ī ─æß╗Ö v├Ā gß╗Źi l├Ā mß╗Öt ─æŲ░ß╗Øng h├¼nh sin. |
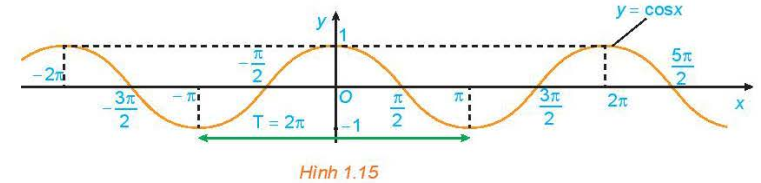
1.4. ─Éß╗ō thß╗ŗ v├Ā t├Łnh chß║źt cß╗¦a h├Ām sß╗æ y = cos x
|
H├Ām sß╗æ y = cos x: - C├│ tß║Łp x├Īc ─æß╗ŗnh l├Ā R v├Ā tß║Łp gi├Ī trß╗ŗ l├Ā [-1; 1]. - L├Ā h├Ām sß╗æ chß║Ąn v├Ā tuß║¦n ho├Ān vß╗øi chu k├¼ \(2\pi\). - ─Éß╗ōng biß║┐n tr├¬n mß╗Śi khoß║Żng \(\left(-{\pi}+k2\pi;k2\pi\right)\), v├Ā nghß╗ŗch biß║┐n tr├¬n mß╗Śi khoß║Żng \(\left(k2\pi;{\pi }+k2\pi\right), k\in \mathbb{Z}\). - C├│ ─æß╗ō thß╗ŗ l├Ā mß╗Öt ─æŲ░ß╗Øng h├¼nh sin ─æß╗æi xß╗®ng qua trß╗źc tung. |
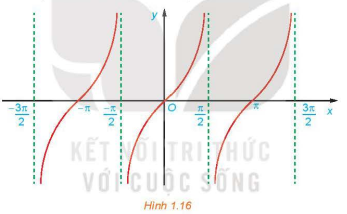
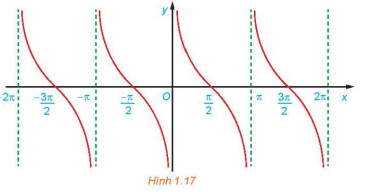
1.5. ─Éß╗ō thß╗ŗ v├Ā t├Łnh chß║źt cß╗¦a h├Ām sß╗æ y = tan x
|
H├Ām sß╗æ y = tan x: - C├│ tß║Łp x├Īc ─æß╗ŗnh l├Ā R \(\backslash\left\{{\pi \over 2}+k\pi|k\in\mathbb{Z}\right\}\) v├Ā tß║Łp gi├Ī trß╗ŗ l├Ā R. - L├Ā h├Ām sß╗æ lß║╗ v├Ā tuß║¦n ho├Ān vß╗øi chu k├¼ \(\pi\). - ─Éß╗ōng biß║┐n tr├¬n mß╗Śi khoß║Żng \(\left(-{\pi \over 2}+k\pi;{\pi \over 2}+k\pi\right), k\in \mathbb{Z}\). - C├│ ─æß╗ō thß╗ŗ l├Ā ─æß╗æi xß╗®ng qua gß╗æc toß║Ī ─æß╗Ö. |
1.6. ─Éß╗ō thß╗ŗ v├Ā t├Łnh chß║źt cß╗¦a h├Ām sß╗æ y = cot x
|
H├Ām sß╗æ y = cot x: - C├│ tß║Łp x├Īc ─æß╗ŗnh l├Ā R \(\backslash\left\{k\pi|k\in\mathbb{Z}\right\}\) v├Ā tß║Łp gi├Ī trß╗ŗ l├Ā R. - L├Ā h├Ām sß╗æ lß║╗ v├Ā tuß║¦n ho├Ān vß╗øi chu k├¼ \(\pi\). - Nghß╗ŗch biß║┐n tr├¬n mß╗Śi khoß║Żng \(\left(k\pi;{\pi}+k\pi\right), k\in \mathbb{Z}\). - C├│ ─æß╗ō thß╗ŗ l├Ā ─æß╗æi xß╗®ng qua gß╗æc toß║Ī ─æß╗Ö. |
B├Āi tß║Łp minh hß╗Źa
C├óu 1: T├¼m tß║Łp x├Īc ─æß╗ŗnh cß╗¦a c├Īc h├Ām sß╗æ: \(y = \frac{{1 + \cos x}}{{\sin x}}\).
HŲ░ß╗øng dß║½n giß║Żi
H├Ām sß╗æ \(y = \frac{{1 + \cos x}}{{\sin x}}\) x├Īc ─æß╗ŗnh khi sinxŌēĀ0ŌćöxŌēĀkŽĆ,kŌłłZ
Vß║Ły tß║Łp x├Īc ─æß╗ŗnh cß╗¦a h├Ām sß╗æ l├Ā \(D = \mathbb{R}\setminus \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\).
C├óu 2: X├Īc ─æß╗ŗnh t├Łnh chß║Ąn lß║╗ cß╗¦a h├Ām sß╗æ \(y = \frac{{\cos2x}}{x}\)
HŲ░ß╗øng dß║½n giß║Żi
Tß║Łp x├Īc ─æß╗ŗnh: D=RŌł¢{0} l├Ā tß║Łp ─æß╗æi xß╗®ng
f(ŌłÆx) =
Vß║Ły y l├Ā h├Ām sß╗æ lß║╗.
Luyß╗ćn tß║Łp B├Āi 3 To├Īn 11 Kß║┐t Nß╗æi Tri Thß╗®c
Hß╗Źc xong b├Āi hß╗Źc n├Āy, em c├│ thß╗ā:
- Nhß║Łn biß║┐t c├Īc kh├Īi niß╗ćm v├Ā ─æß║Ęc trŲ░ng h├¼nh hß╗Źc cß╗¦a h├Ām sß╗æ chß║Ąn, h├Ām sß╗æ lß║╗, h├Ām sß╗æ tuß║¦n ho├Ān, nhß║Łn biß║┐t h├Ām sß╗æ lŲ░ß╗Żng gi├Īc y = sin x, y = cosx, y = tan x, y = cot x th├┤ng qua ─æŲ░ß╗Øng tr├▓n lŲ░ß╗Żng gi├Īc. M├┤ tß║Ż bß║Żng gi├Ī trß╗ŗ cß╗¦a bß╗æn h├Ām sß╗æ lŲ░ß╗Żng gi├Īc ─æ├│ tr├¬n mß╗Öt chu k├¼.
- Giß║Żi th├Łch tß║Łp x├Īc ─æß╗ŗnh; tß║Łp gi├Ī trß╗ŗ; t├Łnh chß║źt chß║Ąn, lß║╗; t├Łnh tuß║¦n ho├Ān; chu k├¼; khoß║Żng ─æß╗ōng biß║┐n, nghß╗ŗch biß║┐n cß╗¦a c├Īc h├Ām sß╗æ, vß║Į ─æß╗ō thß╗ŗ cß╗¦a c├Īc h├Ām sß╗æ y = sin x, y = cos x, y = tan x, y = cotx.
- Giß║Żi quyß║┐t mß╗Öt sß╗æ vß║źn ─æß╗ü thß╗▒c tiß╗ģn gß║»n vß╗øi h├Ām sß╗æ lŲ░ß╗Żng gi├Īc.
3.1. Trß║»c nghiß╗ćm B├Āi 3 To├Īn 11 Kß║┐t Nß╗æi Tri Thß╗®c
C├Īc em c├│ thß╗ā hß╗ć thß╗æng lß║Īi nß╗Öi dung kiß║┐n thß╗®c ─æ├Ż hß╗Źc ─æŲ░ß╗Żc th├┤ng qua b├Āi kiß╗ām tra Trß║»c nghiß╗ćm To├Īn 11 Kß║┐t nß╗æi tri thß╗®c ChŲ░ŲĪng 1 B├Āi 3 cß╗▒c hay c├│ ─æ├Īp ├Īn v├Ā lß╗Øi giß║Żi chi tiß║┐t.
-
- A. T = ŽĆ.
- B. T = 2ŽĆ.
- C. T = ŽĆ2.
- D. T = ŽĆ/2.
-
- A. T = ŽĆ.
- B. T = 2ŽĆ.
- C. T = 3ŽĆ.
- D. T = 6ŽĆ.
-
- A. y = sinx/2
- B. y = cosx/2
- C. y = - cosx/4
- D. y = sin( - x/2)
C├óu 4-10: Mß╗Øi c├Īc em ─æ─āng nhß║Łp xem tiß║┐p nß╗Öi dung v├Ā thi thß╗Ł Online ─æß╗ā cß╗¦ng cß╗æ kiß║┐n thß╗®c vß╗ü b├Āi hß╗Źc n├Āy nh├®!
3.2. B├Āi tß║Łp SGK B├Āi 3 To├Īn 11 Kß║┐t Nß╗æi Tri Thß╗®c
C├Īc em c├│ thß╗ā xem th├¬m phß║¦n hŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp To├Īn 11 Kß║┐t nß╗æi tri thß╗®c ChŲ░ŲĪng 1 B├Āi 3 ─æß╗ā gi├║p c├Īc em nß║»m vß╗»ng b├Āi hß╗Źc v├Ā c├Īc phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp.
Mß╗¤ ─æß║¦u trang 22 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Hoß║Īt ─æß╗Öng 1 trang 22 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Luyß╗ćn tß║Łp 1 trang 23 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Hoß║Īt ─æß╗Öng 2 trang 23 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Luyß╗ćn tß║Łp 2 trang 24 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Hoß║Īt ─æß╗Öng 3 trang 24 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Giß║Żi C├óu hß╗Åi trang 24 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Luyß╗ćn tß║Łp 3 trang 25 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Hoß║Īt ─æß╗Öng 4 trang 25 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Luyß╗ćn tß║Łp 4 trang 26 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Vß║Łn dß╗źng 1 trang 26 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Hoß║Īt ─æß╗Öng 5 trang 26 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Luyß╗ćn tß║Łp 5 trang 27 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Vß║Łn dß╗źng 2 trang 27 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Hoß║Īt ─æß╗Öng 6 trang 28 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Luyß╗ćn tß║Łp 6 trang 29 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Hoß║Īt ─æß╗Öng 7 trang 29 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Luyß╗ćn tß║Łp 7 trang 30 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Giß║Żi B├Āi 1.15 trang 30 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Giß║Żi B├Āi 1.16 trang 30 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Giß║Żi B├Āi 1.17 trang 30 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Giß║Żi B├Āi 1.18 trang 30 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Giß║Żi B├Āi 1.19 trang 30 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Ba╠Ći t├ó╠Żp 1.16 trang 17 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Ba╠Ći t├ó╠Żp 1.17 trang 17 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Ba╠Ći t├ó╠Żp 1.18 trang 18 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Ba╠Ći t├ó╠Żp 1.19 trang 18 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Ba╠Ći t├ó╠Żp 1.20 trang 18 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Ba╠Ći t├ó╠Żp 1.21 trang 18 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Ba╠Ći t├ó╠Żp 1.22 trang 18 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Ba╠Ći t├ó╠Żp 1.23 trang 18 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Ba╠Ći t├ó╠Żp 1.24 trang 19 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Hß╗Åi ─æ├Īp B├Āi 3 To├Īn 11 Kß║┐t Nß╗æi Tri Thß╗®c
Trong qu├Ī tr├¼nh hß╗Źc tß║Łp nß║┐u c├│ thß║»c mß║»c hay cß║¦n trß╗Ż gi├║p g├¼ th├¼ c├Īc em h├Ży comment ß╗¤ mß╗źc Hß╗Åi ─æ├Īp, Cß╗Öng ─æß╗ōng To├Īn hß╗Źc HOC247 sß║Į hß╗Ś trß╗Ż cho c├Īc em mß╗Öt c├Īch nhanh ch├│ng!
Ch├║c c├Īc em hß╗Źc tß║Łp tß╗æt v├Ā lu├┤n ─æß║Īt th├Ānh t├Łch cao trong hß╗Źc tß║Łp!
-- Mod To├Īn Hß╗Źc 11 Hß╗īC247