Hoạt động 2 trang 23 SGK Toán 11 Kết nối tri thức tập 1 - KNTT

Cho hai hàm số \(f\left( x \right) = {x^2},g\left( x \right) = {x^3}\) với các đồ thị như hình dưới đây.

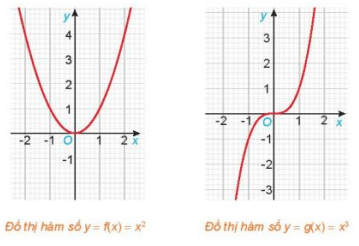
a) Tìm các tập xác định \({D_f},\:{D_g}\) của các hàm số f(x) và g(x).

b) Chứng tỏ rằng \(f\left( { - x} \right) = f\left( x \right),\:\forall x \in {D_f}\). Có nhận xét gì về tính đối xứng của đồ thị hàm số y=f(x) đối với hệ trục tọa độ Oxy?

c) Chứng tỏ rằng \(g\left( { - x} \right) =  - g\left( x \right),\:\forall x \in {D_g}\). Có nhận xét gì về tính đối xứng của đồ thị hàm số y=g(x) đối với hệ trục tọa độ Oxy?