Giải bài 2 tr 99 sách GK Toán ĐS lớp 10
Biểu diễn hình học tập nghiệm của các hệ bất phương trình hai ẩn sau.
a) \(\left\{\begin{matrix} x-2y<0\\ x+3y>-2 \\ y-x<3; \end{matrix}\right.\)
b) \(\left\{\begin{matrix} \frac{x}{3}+\frac{y}{2}-1<0\\ x+\frac{1}{2}-\frac{3y}{2}\leq 2 \\ x\geq 0. \end{matrix}\right.\)
Hướng dẫn giải chi tiết bài 2
Câu a:
Ta có: \(\left\{ {\begin{array}{*{20}{c}}
{x - 2y < 0}\\
{x + 3y > - 2}\\
{y - x < 3}
\end{array}} \right. \Leftrightarrow \left\{ \begin{array}{l}
x - 2y < 0\\
x + 3y > - 2\\
y - x < 3
\end{array} \right.\)
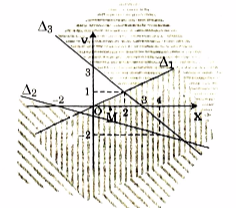
Gọi \({\Delta _1},{\Delta _2},{\Delta _3}\) lần lượt là ba đường thẳng có phương trình là:
\(x - 2y = 0;x + 3y + 2 = 0;\)
x - y + 3 = 0
Lấy điểm M(1;0), ta có:
1 - 2.0 = 1 > 0
1 + 3.0 + 2 = 3 >0;
1 - 0 + 3 = 4 > 0
Vẽ \({\Delta _1},{\Delta _2},{\Delta _3}\) trên hệ trục, ta có:
Vậy tập nghiệm của hệ là miền không gạch
Câu b:
\(\left\{ \begin{array}{l}
\frac{x}{3} + \frac{y}{2} - 1 < 0\\
x + \frac{1}{2} - \frac{{3y}}{2} \le 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
2x + 3y - 6 < 0\\
2x - 3y - 3 \le 0\\
x \ge 0
\end{array} \right.\)
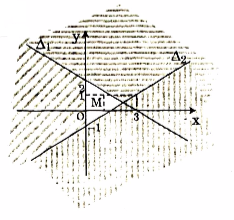
Gọi \({\Delta _1},{\Delta _2},{\Delta _3}\) lần lượt là ba đường thẳng có phương trình lần lượt là 2x + 3y - 6 =0;
2x - 3y - 3 = 0; x = 0.
Lấy điểm M(1;1), ta có:
2.1 + 3.1 - 6= -1< 0
2.1 - 3.1 - 3 =-4 < 0; 1 >0
Vẽ \({\Delta _1},{\Delta _2},{\Delta _3}\) trên hệ trục ta có:
⇒ Trên nghiệm của hệ là miền trong của tam giác \({M _1},{M _2},{M _3}\) và hai đoạn thẳng M1M2, M2M3. Với M1 là giao của {\Delta _1} và {\Delta _3}, M2 là giao {\Delta _2},{\Delta _3}M3 là giao của {\Delta _1} và {\Delta _2}.
-- Mod Toán 10 HỌC247
Video hướng dẫn giải bài 2 SGK
-


Biểu diễn hình học tập nghiệm của hệ bất phương trình hai ẩn sau: \(\left\{ {\begin{array}{*{20}{c}} {\frac{x}{3} + \frac{y}{2} - 1 < 0}\\ {x + \frac{1}{2} - \frac{{3y}}{2} \le 2}\\ {x \ge 0} \end{array}} \right.\)
bởi thu thủy
 19/02/2021
Theo dõi (0) 1 Trả lời
19/02/2021
Theo dõi (0) 1 Trả lời -


Biểu diễn hình học tập nghiệm của hệ bất phương trình hai ẩn sau: \(\left\{ {\begin{array}{*{20}{c}} {x - 2y < 0}\\ {x + 3y > - 2}\\ {y - x < 3} \end{array}} \right.\)
bởi Tường Vi
 19/02/2021
Theo dõi (0) 1 Trả lời
19/02/2021
Theo dõi (0) 1 Trả lời -


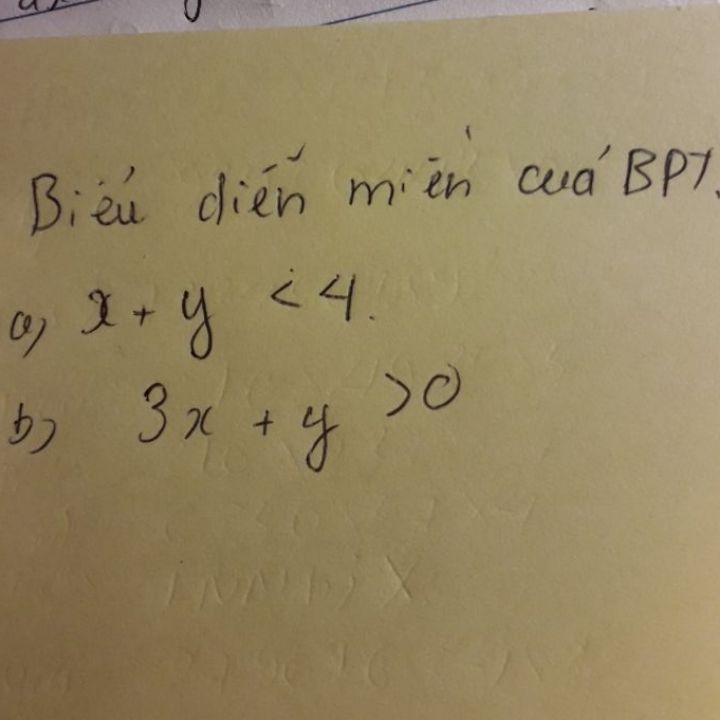 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải bất phương trình \(\frac{{\left( {2x - 1} \right)\left( {{x^2} + 1} \right)}}{{4{x^2} + x - 3}} \ge 0\)?
bởi Vũ tú Uyên
 07/07/2020
07/07/2020
Giải bất phương trình
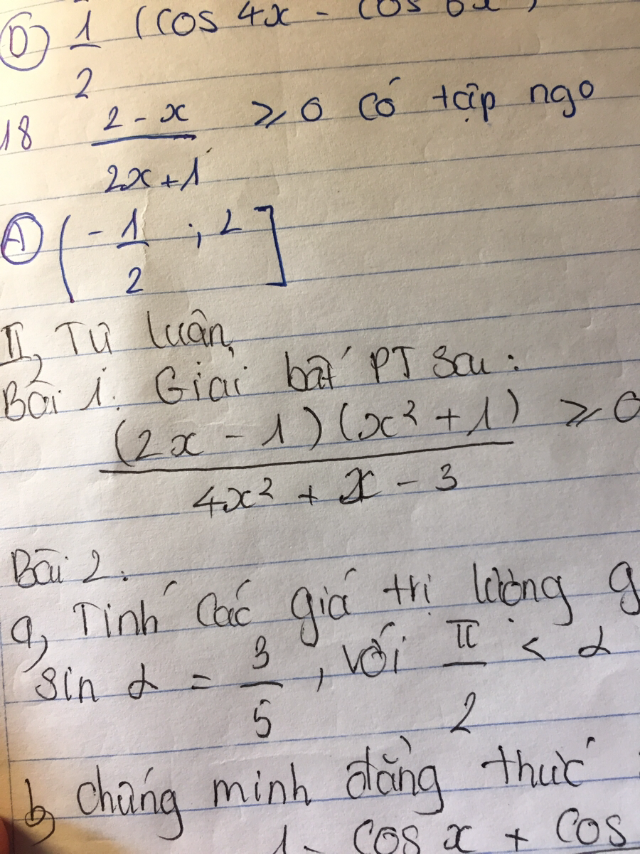 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời
Bài tập SGK khác
Bài tập 1 trang 99 SGK Đại số 10
Bài tập 3 trang 99 SGK Đại số 10
Bài tập 4.46 trang 116 SBT Toán 10
Bài tập 4.47 trang 116 SBT Toán 10
Bài tập 4.48 trang 117 SBT Toán 10
Bài tập 4.49 trang 117 SBT Toán 10
Bài tập 4.50 trang 117 SBT Toán 10
Bài tập 42 trang 132 SGK Toán 10 NC
Bài tập 43 trang 132 SGK Toán 10 NC
Bài tập 44 trang 132 SGK Toán 10 NC
Bài tập 45 trang 135 SGK Toán 10 NC
Bài tập 46 trang 135 SGK Toán 10 NC





