Giải bài 3 tr 99 sách GK Toán ĐS lớp 10
Có ba nhóm máy A, B, C dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một đơn vị sản phẩm mỗi loại phải lần lượt dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và số máy của từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được cho trong bảng sau:

Một đơn vị sản phẩm I lãi 3 nghìn đồng, một sản phẩm II lãi 5 nghìn đồng. Hãy lập phương án để việc sản xuất hai loại sản phẩm trên có lãi cao nhất.
Hướng dẫn giải chi tiết bài 3
Gọi x là số đơn vị sản phẩm loại I(x > 0), y là số đơn vị sản phẩm loại II(y>0). Như vậy tiền lãi mỗi ngày là L =3.x + 5y (nghìn đồng).
Theo bảng, ta có: Nhóm A cần 2x + 2y máy.
Nhóm B cần 0x + 2y máy.
Nhóm C cần 2x + 4y máy.
Theo bài ra, ta có hệ:
\(\left\{ {\begin{array}{*{20}{l}}
{2x + 2y \le 10}\\
{2y \le 4}\\
{2x + 4y \le 12}
\end{array}} \right.{\rm{ }}(1){\mkern 1mu} (x \ge 0;y \ge 0)\)
Bài toán trở thành: trong các nghiệm của hệ bất phương trình (1) thì nghiệm \((x = {x_0};y = {y_0})\) sao cho L = 3x + 5y lớn nhất.
Miền nghiệm của hệ (1) là ngũ giác OABCD kể cả miền trong (gọi là miền ngũ giác OABCD).
Do vậy để có tổng tiền cao nhất thì x = 4, y = 1 và L=3.4 + 5.1 = 17 (nghìn đồng).
Vậy đề có tiền lãi cao nhất, mỗi ngày sản xuất 4 đơn vị sản phẩm loại I và 1 đơn vị sản phẩm loại II.
.png)
-- Mod Toán 10 HỌC247
Video hướng dẫn giải bài 3 SGK
-


Giải bất phương trình \(\left( {\sqrt {3{x^2} - x + 1} - x - 2} \right).\sqrt {{x^2} - 6x + 8} < 0\)?
bởi An Thu Nguyễn
 26/06/2020
26/06/2020
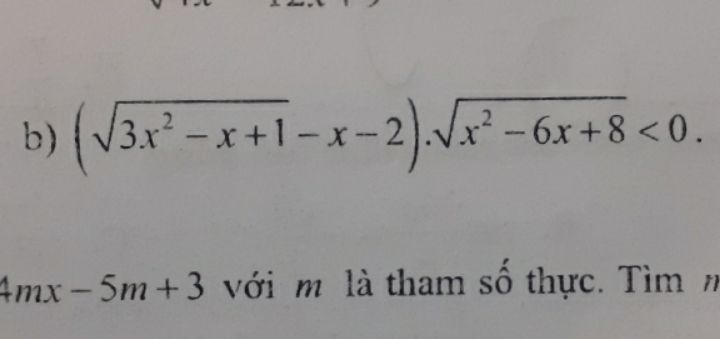 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chứng minh rằng \(\frac{{7x + 9y}}{{\sqrt {252} }} \ge \sqrt {xy} \) với x, y >0?
bởi Ny To
 13/06/2020
13/06/2020
Giúp mik bài này vs
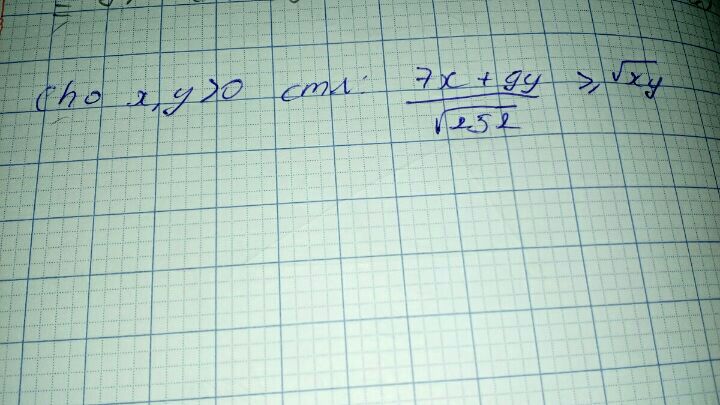 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải bpt \(9 - {x^2} \le 0\)?
bởi Nguyễn Hannah
 09/06/2020
09/06/2020
 Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -


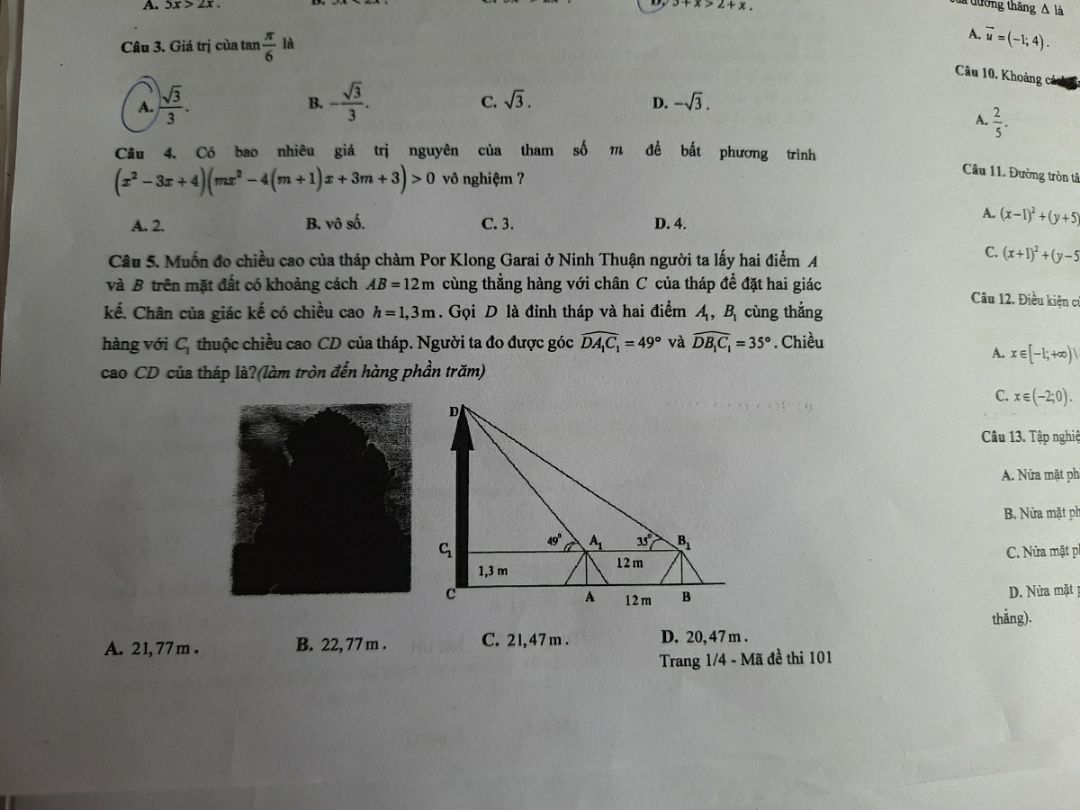
Giúp mình bài này với
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 1 trang 99 SGK Đại số 10
Bài tập 2 trang 99 SGK Đại số 10
Bài tập 4.46 trang 116 SBT Toán 10
Bài tập 4.47 trang 116 SBT Toán 10
Bài tập 4.48 trang 117 SBT Toán 10
Bài tập 4.49 trang 117 SBT Toán 10
Bài tập 4.50 trang 117 SBT Toán 10
Bài tập 42 trang 132 SGK Toán 10 NC
Bài tập 43 trang 132 SGK Toán 10 NC
Bài tập 44 trang 132 SGK Toán 10 NC
Bài tập 45 trang 135 SGK Toán 10 NC
Bài tập 46 trang 135 SGK Toán 10 NC





