Giải bài 4.47 tr 116 SBT Toán 10
Một hộ nông dân trồng đậu và cà trên diện tích 8a. Nếu trồng đậu thì cần 20 công và thu 3 000 000 đồng trên một a, nếu trồng cà thì cần 30 công và thu 40 000 000 đồng trên một a. Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được nhiều tiền nhất khi tổng số công không quá 180?
Hướng dẫn giải chi tiết
Gọi x là diện tích trồng đậu, y là diện tích trồng cà, (đơn vị a = 100 m2), điều kiện x ≥ 0, y ≥ 0, ta có x + y ≤ 0
Số công cần dùng là 20x + 30y ≤ 180 hay 20 + 3y ≤ 18
Số tiền thu được là
F = 3000000x + 4000000y (đồng)
Hay F = 3x + 4y (đồng)
Ta cần tìm x, y thỏa mãn hệ bất phương trình
\(\left\{ \begin{array}{l}
x + y \le \\
2x + 3y \le 18\\
x \ge 0\\
y \ge 0
\end{array} \right.\)
Sao cho F = 3x + 4y đạt giá trị lớn nhất.
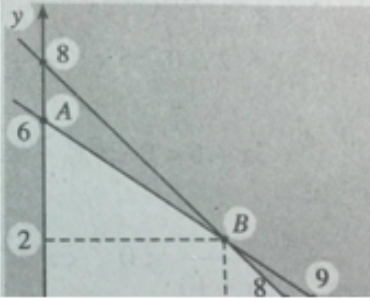
Biểu diễn tập nghiệm của (H) ta được miền tứ giác OABC với A(0;6), B(6;2), C(8;0) và O(0;0).
Xét giá trị của F tại các đỉnh O, A, B, C và so sánh ta suy ra x = 6, y = 2 (tọa độ điểm B) là diện tích cần trồng mỗi loại để thu được nhiều tiền nhất là F = 26 (triệu đồng).
Đáp số: Trồng 6a đậu, 2a cà, thu hoạch 26 000 000 đồng.
-- Mod Toán 10 HỌC247
-


Tính số tiền lãi cao nhất mà người nông dân thu được
bởi Tiến Phan
 26/04/2020
Câu 13
26/04/2020
Câu 13 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải bất phương trình x/3+(x-1)/2<(3-2x)/4
bởi Trang Cao
 25/04/2020
giải câu 1
25/04/2020
giải câu 1 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải bất phương trình x+(2-x)/3>=x/5
bởi Trang Cao
 25/04/2020
giải câu 1
25/04/2020
giải câu 1 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm x biết |7-2x|=|5-3x|+|x+2|
bởi Ngọc Anh Ngo
 20/04/2020
20/04/2020
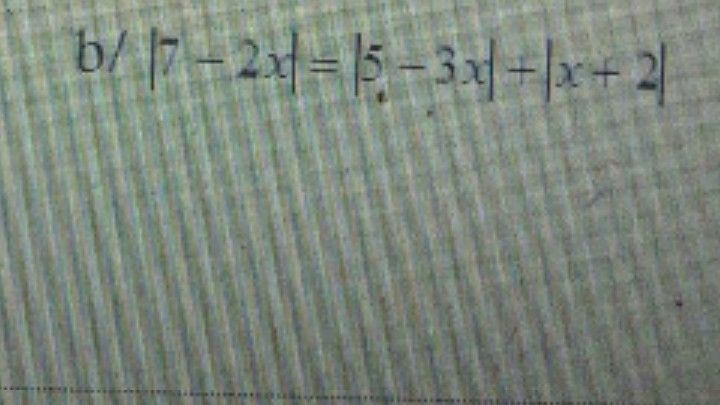 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời
Bài tập SGK khác
Bài tập 3 trang 99 SGK Đại số 10
Bài tập 4.46 trang 116 SBT Toán 10
Bài tập 4.48 trang 117 SBT Toán 10
Bài tập 4.49 trang 117 SBT Toán 10
Bài tập 4.50 trang 117 SBT Toán 10
Bài tập 42 trang 132 SGK Toán 10 NC
Bài tập 43 trang 132 SGK Toán 10 NC
Bài tập 44 trang 132 SGK Toán 10 NC
Bài tập 45 trang 135 SGK Toán 10 NC
Bài tập 46 trang 135 SGK Toán 10 NC