Bài tập 47 trang 135 SGK Toán 10 NC
Gọi (S) là tập hợp các điểm trong mặt phẳng tọa độ có tọa độ thỏa mãn hệ:
\(\left\{ \begin{array}{l}
2x - y \ge 2\\
x - 2y \le 2\\
x + y \le 5\\
x \ge 0
\end{array} \right.\)
a) Hãy xác định (S) để thấy rằng đó là một tam giác.
b) Trong (S) hãy tìm điểm có tọa độ (x;y) làm cho biểu thức f(x;y) = y − x có giá trị nhỏ nhất, biết rằng f(x;y) có giá trị nhỏ nhất tại một trong các đỉnh của (S).
Hướng dẫn giải chi tiết
a) Lần lượt dựng các đường thẳng:
\( - 2x + y = - 2;x - 2y = 2,x + y = 5\) và x = 0
Và dựa vào đó để tìm nghiệm S của hệ bất phương trình
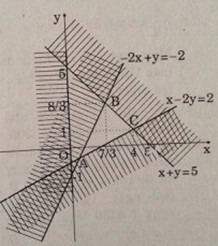
Tập nghiệm S được biểu diễn bằng miền trong của tam giác ABC với:
\(A\left( {\frac{2}{3}; - \frac{2}{3}} \right);B\left( {\frac{7}{3};\frac{8}{3}} \right);C\left( {4;1} \right)\)
b) Tại \(A\left( {\frac{2}{3}; - \frac{2}{3}} \right) \Rightarrow F = - \frac{4}{3}\)
Tại \(B\left( {\frac{7}{3};\frac{8}{3}} \right) \Rightarrow F = \frac{1}{3}\)
Tại C(4'1) thì F = - 3
Vậy F đạt giá trị nhỏ nhất tại C(4;1)
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





