HOC247 mß╗Øi c├Īc em hß╗Źc sinh tham khß║Żo b├Āi T├Łch cß╗¦a mß╗Öt sß╗æ vß╗øi mß╗Öt vectŲĪ b├¬n dŲ░ß╗øi ─æ├óy, th├┤ng qua b├Āi giß║Żng n├Āy c├Īc em dß╗ģ d├Āng hß╗ć thß╗æng lß║Īi to├Ān bß╗Ö kiß║┐n thß╗®c ─æ├Ż hß╗Źc, b├¬n cß║Īnh ─æ├│ c├Īc em c├▓n nß║»m ─æŲ░ß╗Żc phŲ░ŲĪng ph├Īp giß║Żi c├Īc b├Āi tß║Łp v├Ā vß║Łn dß╗źng v├Āo giß║Żi c├Īc b├Āi tß║Łp tŲ░ŲĪng tß╗▒. Ch├║c c├Īc em c├│ mß╗Öt tiß║┐t hß╗Źc thß║Łt hay v├Ā thß║Łt vui khi ─æß║┐n lß╗øp!
T├│m tß║»t l├Į thuyß║┐t
1.1. ─Éß╗ŗnh ngh─®a
|
+) T├Łch cß╗¦a mß╗Öt sß╗æ thß╗▒c \(k\) vß╗øi mß╗Öt vecto \(\overrightarrow a \ne \overrightarrow 0 \) l├Ā mß╗Öt vecto, k├Ł kiß╗ću l├Ā \(k\overrightarrow a .\) +) Vecto \(k\overrightarrow a \) c├│ ─æß╗Ö d├Āi bß║▒ng \(\left| k \right|\left| {\overrightarrow a } \right|\) v├Ā c├╣ng hŲ░ß╗øng vß╗øi vecto \(\overrightarrow a \) nß║┐u \(k > 0\), ngŲ░ß╗Żc hŲ░ß╗øng vß╗øi vecto \(\overrightarrow a \) nß║┐u \(k < 0\) |
|---|
+) Quy Ų░ß╗øc: \(0\;\overrightarrow a = \overrightarrow 0 \) v├Ā \(k\;\overrightarrow 0 = \overrightarrow 0 \)
V├Ł dß╗ź: Cho B l├Ā trung ─æiß╗ām cß╗¦a ─æoß║Īn thß║Żng AC. T├¼m sß╗æ k trong mß╗Śi trŲ░ß╗Øng hß╗Żp sau:
a) \(\overrightarrow {CA} = k\overrightarrow {CB} \)
b) \(\overrightarrow {CA} = k\overrightarrow {AB} \)
Giß║Żi
Ta c├│: \(\overrightarrow {CA} ,\overrightarrow {CB} \) l├Ā hai vectŲĪ c├╣ng phŲ░ŲĪng v├Ā \(\left| {\overrightarrow {CA} } \right| = 2\left| {\overrightarrow {CB} } \right|\)
Suy ra \(\overrightarrow {CA} = 2\overrightarrow {CB} \). Vß║Ły k = 2
b) Ta c├│: \(\overrightarrow {CA} ,\overrightarrow {AB} \) l├Ā hai vectŲĪ ngŲ░ß╗Żc hŲ░ß╗øng v├Ā \(\left| {\overrightarrow {CA} } \right| = 2\left| {\overrightarrow {AB} } \right|{\rm{ }}\)
Suy ra: \(\overrightarrow {CA} = - 2\overrightarrow {AB} \). Vß║Ły k = -2
1.2. T├Łnh chß║źt
Vß╗øi hai vecto \(\overrightarrow a ,\overrightarrow b \) v├Ā hai sß╗æ thß╗▒c \(k,t\) ta lu├┤n c├│:
\(\begin{array}{l}k(t\overrightarrow a ) = (kt)\;\overrightarrow a \\(k + t)\,\overrightarrow a = k\overrightarrow a + t\overrightarrow a \\k(\overrightarrow a + \overrightarrow b ) = k\overrightarrow a + k\overrightarrow b ;\quad k(\overrightarrow a - \overrightarrow b ) = k\overrightarrow a - k\overrightarrow b \\1\;\overrightarrow a = \overrightarrow a ;\;\;( - 1)\;\overrightarrow a = - \,\overrightarrow a \end{array}\)
V├Ł dß╗ź: Thß╗▒c hiß╗ćn c├Īc ph├®p to├Īn vecto sau:
\(\begin{array}{l}
a)5\left( {\overrightarrow u + \overrightarrow v } \right)\\
b)\left( {x + 2} \right)\overrightarrow a \\
c) - 3\left( {4\overrightarrow e } \right)\\
d)\overrightarrow c - 2\overrightarrow c
\end{array}\)
Giß║Żi
\(\begin{array}{l}
a)5\left( {\overrightarrow u + \overrightarrow v } \right) = 5\overrightarrow u + 5\overrightarrow v \\
b)\left( {x + 2} \right)\overrightarrow a = x\overrightarrow a + 2\overrightarrow a \\
c) - 3\left( {4\overrightarrow e } \right) = \left( { - 3.4} \right)\overrightarrow e = - 12\overrightarrow e \\
d)\overrightarrow c - 2\overrightarrow c = \left( {1 - 2} \right)\overrightarrow c = \left( { - 1} \right)\overrightarrow c = - \overrightarrow c
\end{array}\)
1.3. Mß╗Öt sß╗æ ß╗®ng dß╗źng
- Nß║┐u I l├Ā trung ─æiß╗ām cß╗¦a ─æoß║Īn thß║│ng AB th├¼ \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \) vß╗øi ─æiß╗ām M bß║źt k├¼.
- Nß║┐u G l├Ā trß╗Źng t├óm cß╗¦a tam gi├Īc ABC th├¼ \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 2\overrightarrow {MG} \) vß╗øi ─æiß╗ām M bß║źt k├¼.
* ─Éiß╗üu kiß╗ćn ─æß╗ā hai vectŲĪ c├╣ng phŲ░ŲĪng. ─Éiß╗üu kiß╗ćn ─æß╗ā ba ─æiß╗ām thß║│ng h├Āng.
- ─Éiß╗üu kiß╗ćn cß║¦n v├Ā ─æß╗¦ ─æß╗ā hai vectŲĪ \(\overrightarrow a \) v├Ā \(\overrightarrow b \) (\(\overrightarrow b \ne \overrightarrow 0 \)) c├╣ng phŲ░ŲĪng l├Ā c├│ mß╗Öt sß╗æ thß╗▒c k ─æß╗ā \(\overrightarrow a = k\overrightarrow b \).
- ─Éiß╗üu kiß╗ćn cß║¦n v├Ā ─æß╗¦ ─æß╗ā ba ─æiß╗ām ph├ón biß╗ćt A, B, C thß║│ng h├Āng l├Ā c├│ sß╗æ thß╗▒c k ─æß╗ā \(\overrightarrow {AB} = k\overrightarrow {AC} \).
V├Ł dß╗ź: Cho tam gi├Īc OAB. ─Éiß╗ām M thuß╗Öc cß║Īnh AB sao cho \(AM = \frac{2}{3}AB\). Kß║╗ MH // OB, MK // OA (H├¼nh sau).
Giß║Ż sß╗Ł \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \).
a) Biß╗āu thß╗ŗ \(\overrightarrow {OH}\) theo \(\overrightarrow {a}\) v├Ā \(\overrightarrow {OK}\) theo \(\overrightarrow {b}\).
b) Biß╗āu thß╗ŗ \(\overrightarrow {OM}\) theo \(\overrightarrow {a}\) v├Ā \(\overrightarrow {b}\).
Giß║Żi
a) Ta c├│: MH // OB, MK // OA suy ra
\(\frac{{OK}}{{OB}} = \frac{{AM}}{{AB}} = \frac{2}{3},\frac{{OH}}{{OA}} = \frac{{BM}}{{AB}} = \frac{1}{3}\)
V├¼ \(\overrightarrow {OH}\) v├Ā \(\overrightarrow {OA}\) c├╣ng hŲ░ß╗øng v├Ā \(OH = \frac{1}{3}OA\) n├¬n
\(\overrightarrow {OH} = \frac{1}{3}\overrightarrow {OA} = \frac{1}{3}\overrightarrow a \)
V├¼ \(\overrightarrow {OK}\) v├Ā \(\overrightarrow {OB}\) c├╣ng hŲ░ß╗øng v├Ā \(OK = \frac{2}{3}OB\) n├¬n
\(\overrightarrow {OK} = \frac{2}{3}\overrightarrow {OB} = \frac{2}{3}\overrightarrow b \)
b) V├¼ tß╗® gi├Īc OHMK l├Ā h├¼nh b├¼nh h├Ānh n├¬n
\(\overrightarrow {OM} = \overrightarrow {OH} + \overrightarrow {OK} = \frac{1}{3}\overrightarrow a + \frac{2}{3}\overrightarrow b \).
B├Āi tß║Łp minh hß╗Źa
C├óu 1: Cho ba ─æiß╗ām A, B, C. Chß╗®ng minh \(3\left( {\overrightarrow {AB} + 2\overrightarrow {BC} } \right) - 2\left( {\overrightarrow {AB} + 3\overrightarrow {BC} } \right) = \overrightarrow {AB} \)
HŲ░ß╗øng dß║½n giß║Żi
Ta c├│: \(3\left( {\overrightarrow {AB} + 2\overrightarrow {BC} } \right) - 2\left( {\overrightarrow {AB} + 3\overrightarrow {BC} } \right)\)\( = 3\overrightarrow {AB} + 3.\left( {2\overrightarrow {BC} } \right) - \left[ {2\overrightarrow {AB} + 2.\left( {3\overrightarrow {BC} } \right)} \right]\)
\( = 3\overrightarrow {AB} + 6.\overrightarrow {BC} - \left( {2\overrightarrow {AB} + 6.\overrightarrow {BC} } \right)\)\( = 3\overrightarrow {AB} + 6.\overrightarrow {BC} - 2\overrightarrow {AB} - 6.\overrightarrow {BC} \)
\( = \left( {3\overrightarrow {AB} - 2\overrightarrow {AB} } \right) + \left( {6.\overrightarrow {BC} - 6.\overrightarrow {BC} } \right) = \overrightarrow {AB} .\)
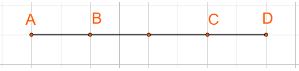
C├óu 2: ß╗× h├¼nh sau, t├¼m k trong mß╗Śi trŲ░ß╗Øng hß╗Żp sau:
a) \(\overrightarrow {AC} = k.\overrightarrow {AD} \)
b) \(\overrightarrow {BD} = k.\overrightarrow {DC} \)
HŲ░ß╗øng dß║½n giß║Żi
a) Ta c├│: \(\overrightarrow {AC} ,\overrightarrow {AD} \)l├Ā hai vecto c├╣ng hŲ░ß╗øng v├Ā \(\left| {\overrightarrow {AC} } \right| = \frac{3}{4}\left| {\overrightarrow {AD} } \right|\)
Suy ra \(\overrightarrow {AC} = \frac{3}{4}\overrightarrow {AD} .\) Vß║Ły \(k = \frac{3}{4}.\)
b) Ta c├│: \(\overrightarrow {BD} ,\overrightarrow {DC} \)l├Ā hai vecto ngŲ░ß╗Żc hŲ░ß╗øng v├Ā \(\left| {\overrightarrow {BD} } \right| = 3\left| {\overrightarrow {DC} } \right|\)
Suy ra \(\overrightarrow {BD} = - 3\overrightarrow {DC} .\) Vß║Ły \(k = - 3.\)
Luyß╗ćn tß║Łp B├Āi 5 ChŲ░ŲĪng 4 To├Īn 10 CD
Qua b├Āi giß║Żng tr├¬n, gi├║p c├Īc em hß╗Źc sinh:
- N├¬u ─æŲ░ß╗Żc ─æß╗ŗnh ngh─®a v├Ā t├Łnh chß║źt cß╗¦a t├Łch vectŲĪ vß╗øi mß╗Öt sß╗æ.
- N├¬u ─æŲ░ß╗Żc t├Łnh chß║źt trung ─æiß╗ām cß╗¦a ─æoß║Īn thß║│ng v├Ā t├Łnh chß║źt trß╗Źng t├óm cß╗¦a tam gi├Īc.
- X├Īc ─æß╗ŗnh ─æŲ░ß╗Żc vectŲĪ khi cho trŲ░ß╗øc sß╗æ thß╗▒c k v├Ā vectŲĪ .
- Vß║Łn dß╗źng ─æŲ░ß╗Żc t├Łnh chß║źt trung ─æiß╗ām cß╗¦a ─æoß║Īn thß║│ng, trß╗Źng t├óm cß╗¦a tam gi├Īc ─æß╗ā giß║Żi b├Āi to├Īn ─æŲĪn giß║Żn.
3.1. B├Āi tß║Łp trß║»c nghiß╗ćm B├Āi 5 ChŲ░ŲĪng 4 To├Īn 10 CD
─Éß╗ā cß╗¦ng cß╗æ b├Āi hß╗Źc xin mß╗Øi c├Īc em c├╣ng l├Ām B├Āi kiß╗ām tra Trß║»c nghiß╗ćm To├Īn 10 C├Īnh Diß╗üu ChŲ░ŲĪng 4 B├Āi 5 ─æß╗ā kiß╗ām tra xem m├¼nh ─æ├Ż nß║»m ─æŲ░ß╗Żc nß╗Öi dung b├Āi hß╗Źc hay chŲ░a.
-
- A. \(\overrightarrow{A I}=\frac{3}{5} \vec{a}+\frac{2}{5} \vec{b}, \overrightarrow{A J}=\frac{5}{3} \vec{a}-\frac{2}{3} \vec{b}\)
- B. \(\overrightarrow{A I}=\frac{3}{5} \vec{a}-\frac{2}{5} \vec{b}, \overrightarrow{A J}=\frac{5}{3} a-\frac{2}{3} \vec{b}\)
- C. \(\overrightarrow{A I}=\frac{2}{5} \vec{a}+\frac{3}{5} \vec{b}, \overrightarrow{A J}=\frac{5}{3} \vec{a}-\frac{2}{3} \vec{b}\)
- D. \(\overrightarrow{A I}=\frac{3}{5} \vec{a}+\frac{2}{5} \vec{b}, \overrightarrow{A J}=\frac{5}{3} \vec{a}+\frac{2}{3} \vec{b}\)
-
- A. \(\overrightarrow{A G}=\frac{1}{18} \vec{a}+\frac{5}{3} \vec{b}\)
- B. \(\overrightarrow{A G}=\frac{1}{18} \vec{a}+\frac{1}{5} \vec{b}\)
- C. \(\overrightarrow{A G}=\frac{5}{18} \vec{a}+\frac{1}{3} \vec{b}\)
- D. \(\overrightarrow{A G}=\frac{5}{18} \vec{a}-\frac{1}{3} \vec{b}\)
-
- A. \(\overrightarrow{I J}=\frac{3}{4} \overrightarrow{A E}\)
- B. \(\overrightarrow{I J}=\frac{5}{4} \overrightarrow{A E}\)
- C. \(\overrightarrow{I J}=\frac{1}{4} \overrightarrow{A E}\)
- D. \(\overrightarrow{I J}=\frac{1}{3} \overrightarrow{A E}\)
C├óu 4-10: Mß╗Øi c├Īc em ─æ─āng nhß║Łp xem tiß║┐p nß╗Öi dung v├Ā thi thß╗Ł Online ─æß╗ā cß╗¦ng cß╗æ kiß║┐n thß╗®c v├Ā nß║»m vß╗»ng hŲĪn vß╗ü b├Āi hß╗Źc n├Āy nh├®!
3.2. B├Āi tß║Łp SGK B├Āi 5 ChŲ░ŲĪng 4 To├Īn 10 CD
B├¬n cß║Īnh ─æ├│ c├Īc em c├│ thß╗ā xem phß║¦n hŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp To├Īn 10 C├Īnh Diß╗üu ChŲ░ŲĪng 4 B├Āi 5 ─æß╗ā gi├║p c├Īc em nß║»m vß╗»ng b├Āi hß╗Źc v├Ā c├Īc phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp.
Hoß║Īt ─æß╗Öng 1 trang 88 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Hoß║Īt ─æß╗Öng 2 trang 88 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Luyß╗ćn tß║Łp 1 trang 89 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Luyß╗ćn tß║Łp 2 trang 89 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Hoß║Īt ─æß╗Öng 3 trang 90 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Hoß║Īt ─æß╗Öng 4 trang 90 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Luyß╗ćn tß║Łp 3 trang 90 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Hoß║Īt ─æß╗Öng 5 trang 91 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Hoß║Īt ─æß╗Öng 6 trang 91 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Luyß╗ćn tß║Łp 4 trang 91 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Giß║Żi b├Āi 1 trang 92 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Giß║Żi b├Āi 2 trang 92 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Giß║Żi b├Āi 3 trang 92 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Giß║Żi b├Āi 4 trang 92 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Giß║Żi b├Āi 5 trang 92 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Giß║Żi b├Āi 6 trang 92 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Giß║Żi b├Āi 7 trang 92 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Giß║Żi b├Āi 47 trang 99 SBT To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Giß║Żi b├Āi 48 trang 99 SBT To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Giß║Żi b├Āi 49 trang 99 SBT To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Giß║Żi b├Āi 50 trang 99 SBT To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Giß║Żi b├Āi 51 trang 99 SBT To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Giß║Żi b├Āi 52 trang 100 SBT To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Giß║Żi b├Āi 53 trang 100 SBT To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Giß║Żi b├Āi 54 trang 100 SBT To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Giß║Żi b├Āi 55 trang 100 SBT To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Giß║Żi b├Āi 56 trang 100 SBT To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Hß╗Åi ─æ├Īp B├Āi 5 ChŲ░ŲĪng 4 To├Īn 10 CD
Trong qu├Ī tr├¼nh hß╗Źc tß║Łp nß║┐u c├│ thß║»c mß║»c hay cß║¦n trß╗Ż gi├║p g├¼ th├¼ c├Īc em h├Ży comment ß╗¤ mß╗źc Hß╗Åi ─æ├Īp, Cß╗Öng ─æß╗ōng To├Īn HOC247 sß║Į hß╗Ś trß╗Ż cho c├Īc em mß╗Öt c├Īch nhanh ch├│ng!
Ch├║c c├Īc em hß╗Źc tß║Łp tß╗æt v├Ā lu├┤n ─æß║Īt th├Ānh t├Łch cao trong hß╗Źc tß║Łp!
-- Mod To├Īn Hß╗Źc 10 Hß╗īC247