Ôn tập Hình học 11 Chương 1 Phép Dời Hình & Phép Đồng Dạng Trong Mặt Phẳng
Mời các em cùng tham khảo tài liệu Ôn tập Hình học 11 Chương 1 tổng hợp các kiến thức về Phép dời hình và phép đồng dạng trong mặt phẳng thông qua các sơ đồ tư duy, các em sẽ có được cách ghi nhớ bài một cách dễ dàng, hiệu quả cùng một số dạng bài tập cho các em luyện tập. Ngoài ra, HỌC247 cũng cung cấp thêm nội dung chi tiết từng bài học, phần giải bài tập SGK cùng một số bài tập trắc nghiệm để các em có thể tham khảo và ôn tập hiệu quả hơn. Đặc biệt, HỌC247 có tổng hợp nhiều đề kiểm tra 1 tiết Chương 1 từ nhiều trường THPT trên cả nước để các em ôn tập và làm quen với cấu trúc đề thi, đánh giá đúng năng lực của mình, mỗi đề đều kèm theo đáp án và gợi ý giải chi tiết sẽ thuận tiện cho các em tham khảo. Mời các em tham khảo bên dưới nhé.
Đề cương Ôn tập Hình học 11 Chương 1
.png)
A. Tóm tắt lý thuyết
1.1. Tổng quan
1.2. Các ký hiệu
1.3. Biểu thức tọa độ
1.4. Sơ đồ biểu diễn mối liên hệ giữa các phép biến hình
B. Bài tập minh họa
Bài 1: Trong mặt phẳng (Oxy) cho →u=(1;−2)→u=(1;−2)
a) Viết phương trình ảnh của mỗi đường trong trường hợp sau:
+) Đường thẳng a có phương trình: 3x-5y+1=0 ?
+) Đường thẳng b có phương trình: 2x+y+100=0
b) Viết phương trình đường tròn ảnh của đường tròn (C ): x2+y2−4x+y−1=0x2+y2−4x+y−1=0
c) Viết phương trình đường (E) ảnh của (E): x29+y24=1x29+y24=1
d) Viết phương trình ảnh của (H): x216−y29=1x216−y29=1
Hướng dẫn giải
a) Gọi M(x;y) thuộc các đường đã cho và M’(x’;y’) thuộc các đường ảnh của chúng.
Theo công thức tọa độ của phép tịnh tiến ta có: {x′=1+xy′=−2+y⇒{x=x′−1y=y′+2{x′=1+xy′=−2+y⇒{x=x′−1y=y′+2
Thay x, y vào phương trình các đường ta có:
Đường thẳng a’: 3(x’-1)-5(y’+2)+1=0 ⇔⇔3x’-5y’-12=0
Đường thẳng b’: 2(x’-1)+(y’+2)+100=0 hay : 2x’+y’+100=0
b) Đường tròn (C’): (x′−1)2+(y′+2)2−4(x′−1)+y′+2−1=0(x′−1)2+(y′+2)2−4(x′−1)+y′+2−1=0
Hay: x2+y2−6x+5y+10=0x2+y2−6x+5y+10=0
c) Đường (E’): (x′−1)29+(y′+2)24=1⇔(x−1)29+(y+2)24=1(x′−1)29+(y′+2)24=1⇔(x−1)29+(y+2)24=1
d) Đường (H’): (x′−1)216−(y′+2)29=1⇔(x−1)216−(y+2)29=1(x′−1)216−(y′+2)29=1⇔(x−1)216−(y+2)29=1.
Bài 2: Cho điểm M(2;-3). Tìm ảnh của điểm M qua phép đối xứng trục d: y-2x=0.
Hướng dẫn giải
Gọi N(x;y) là điểm đối xứng với M qua d và H là trung điểm của MN thì M,N đối xứng nhau qua d thì điều kiện là: {→MN.→U=0(1)H∈d(2){−−−→MN.→U=0(1)H∈d(2)
Ta có: →MN=(x−2;y+3)→U=(1;2)H=(x+22;y−32)−−−→MN=(x−2;y+3)→U=(1;2)H=(x+22;y−32).
Điều kiện (*) ⇔{(x−2).1+(y+3).2=0x+22=y−32⇔{x+2y+4=0y=x+5⇒{y=13x=−143⇒N=(−143;13).⇔{(x−2).1+(y+3).2=0x+22=y−32⇔{x+2y+4=0y=x+5⇒{y=13x=−143⇒N=(−143;13).
Bài 3: Trong mặt phẳng Oxy cho đường tròn (O;R) : x2+y2+2x−6y+6=0x2+y2+2x−6y+6=0và (E) : x29+y24=1x29+y24=1 điểm I(1;2). Tìm ảnh của (O;R) và (E) qua phép đối xứng tâm I.
Hướng dẫn giải
Gọi M(x;y) là điểm bất kỳ thuộc (O;R) và (E).
M’(x’;y’) là ảnh của M qua phép đối xứng tâm I.
Khi đó I là trung điểm của MM’ nên ta có:
{xI=x+x′2yI=y+y′2⇔{x′=2.1−xy′=2.2−y⎧⎨⎩xI=x+x′2yI=y+y′2⇔{x′=2.1−xy′=2.2−y
⇒{x=2−x′y=4−y′⇒[(2−x′)2+(4−y′)2+2(2−x′)−6(4−y′)+6=0(2−x′)29+(4−y′)24=1⇒{x=2−x′y=4−y′⇒⎡⎣(2−x′)2+(4−y′)2+2(2−x′)−6(4−y′)+6=0(2−x′)29+(4−y′)24=1
⇔[x2+y2−6x−2y+6=0(2−x)29+(4−y)24=1⇔[x2+y2−6x−2y+6=0(2−x)29+(4−y)24=1
Vậy ảnh của (O;R) và (E) qua phép đối xứng tâm I có phương trình lần lượt là:
x2+y2−6x−2y+6=0;(2−x)29+(4−y)24=1x2+y2−6x−2y+6=0;(2−x)29+(4−y)24=1.
Bài 4: Trong mặt phẳng tọa độ Oxy, cho đường tròn (O): (x−1)2+(y−1)2=4.(x−1)2+(y−1)2=4. Tìm phương trình đường tròn (O’) là ảnh của (O) qua phép vị tự tâm O tỉ số k=2.
Hướng dẫn giải
Tâm I của (O) có tọa độ I(1;1) bán kính R = 2.
Nếu (O’) có tâm là J và bán kính R’ là ảnh của (O) qua phép vị tự tâm O ta có đẳng thức vectơ:
→OJ=2→OI⇔{x′−0=2.1y′−0=2.1⇒{x′=2y′=2⇒J(2;2)−→OJ=2−→OI⇔{x′−0=2.1y′−0=2.1⇒{x′=2y′=2⇒J(2;2).
R’ = 2R = 2.2 = 4.
Vậy (O’): (x−2)2+(y−2)2=16(x−2)2+(y−2)2=16.
Trắc nghiệm Hình học 11 Chương 1
- Trắc nghiệm Toán 11 Chương 1 Bài 1
- Trắc nghiệm Toán 11 Chương 1 Bài 2
- Trắc nghiệm Toán 11 Chương 1 Bài 3
- Trắc nghiệm Toán 11 Chương 1 Bài 4
- Trắc nghiệm Toán 11 Chương 1 Bài 5
- Trắc nghiệm Toán 11 Chương 1 Bài 6
- Trắc nghiệm Toán 11 Chương 1 Bài 7
- Trắc nghiệm Toán 11 Chương 1 Bài 8
- Trắc nghiệm ôn tập Chương 1 Toán 11
Đề kiểm tra Hình học 11 Chương 1
Đề kiểm tra trắc nghiệm online Chương 1 Hình học 11 (Thi Online)
Phần này các em được làm trắc nghiệm online trong vòng 45 phút để kiểm tra năng lực và sau đó đối chiếu kết quả và xem đáp án chi tiết từng câu hỏi.
- Đề trắc nghiệm ôn tập Chương Phép dời hình và phép đồng dạng trong mặt phẳng
- 40 câu trắc nghiệm ôn tập Chương 1 Hình học 11
- Đề kiểm tra 1 tiết Chương 1 Hình học 11 Trường THPT Lý Thường Kiệt - Bình Thuận
- Đề kiểm tra 1 tiết Chương 1 Hình học 11 năm 2018 Trường THPT Thị Xã Quảng Trị
- Đề kiểm tra 1 tiết Hình học 11 Chương 1 Phép biến hình
Đề kiểm tra Chương 1 Hình học 11 (Tải File)
Phần này các em có thể xem online hoặc tải file đề thi về tham khảo gồm đầy đủ câu hỏi và đáp án làm bài.
- Đề kiểm tra 1 tiết chương 1 Hình học lớp 11 Trường THPT Lý Thường Kiệt năm 2018-2019
- Đề kiểm tra 1 tiết chương 1 Hình học 11 Trường THPT Đoàn Thượng năm học 2018 - 2019
- Đề kiểm tra 1 tiết Chương 1 Hình học 11 Trường THPT ĐĂK GLONG năm học 2018 - 2019
- Đề kiểm tra 1 tiết Chương 1 Hình học 11 năm 2018 có đáp án - Trường THPT Thị xã Quảng Trị
- Đề kiểm tra 1 tiết chương 1 Hình học 11 Trường THPT TX Quảng Trị năm học 2017 - 2018
- Đề kiểm tra 1 tiết chương 1 Hình học 11 năm 2017 có đáp án - Trường THPT Đức Hòa
- Đề kiểm tra 1 tiết Chương 1 Hình học 11
- Ma trận đề kiểm tra 1 tiết Chương 1 Phép biến hình Toán 11
- Đề kiểm tra 1 tiết Chương 1 Hình 11 năm 2017 của Sở GD và ĐT Cà Mau có đáp án
- Đề kiểm tra 1 tiết Chương 1 Hình hoc 11 năm 2017 - Trường THPT Cây Dương có đáp án
- Đề kiểm tra 1 tiết Chương 1 Hình học 11 năm 2017- Trường THPT Hải Lăng có đáp án
Lý thuyết từng bài Chương 1 và hướng dẫn giải bài tập SGK
Lý thuyết các bài học Hình học 11 Chương 1
- Hình học 11 Bài 1 Phép biến hình
- Hình học 11 Bài 2 Phép tịnh tiến
- Hình học 11 Bài 3 Phép đối xứng trục
- Hình học 11 Bài 4 Phép đối xứng tâm
- Hình học 11 Bài 5 Phép quay
- Hình học 11 Bài 6 Khái niệm về phép dời hình và hai hình bằng nhau
- Hình học 11 Bài 7 Phép vị tự
- Hình học 11 Bài 8 Phép đồng dạng
- Hình học 11 Ôn tập chương 1 Phép dời hình và Phép đồng dạng trong mặt phẳng
Hướng dẫn giải bài tập Hình học 11 Chương 1
- Giải bài tập Toán 11 Chương 1 Bài 2
- Giải bài tập Toán 11 Chương 1 Bài 3
- Giải bài tập Toán 11 Chương 1 Bài 4
- Giải bài tập Toán 11 Chương 1 Bài 5
- Giải bài tập Toán 11 Chương 1 Bài 6
- Giải bài tập Toán 11 Chương 1 Bài 7
- Giải bài tập Toán 11 Chương 1 Bài 8
- Giải bài ôn tập Chương 1 Toán 11
Trên đây là tài liệu Ôn tập Hình học 11 Chương 1. Hy vọng với tài liệu này, các em sẽ giúp các em ôn tập và hệ thống lại kiến thức Chương 1 thật tốt. Để thi online và tải file đề thi về máy các em vui lòng đăng nhập vào trang hoc247.net và ấn chọn chức năng "Thi Online" hoặc "Tải về". Ngoài ra, các em còn có thể chia sẻ lên Facebook để giới thiệu bạn bè cùng vào học, tích lũy thêm điểm HP và có cơ hội nhận thêm nhiều phần quà có giá trị từ HỌC247 !







.PNG)
.PNG)
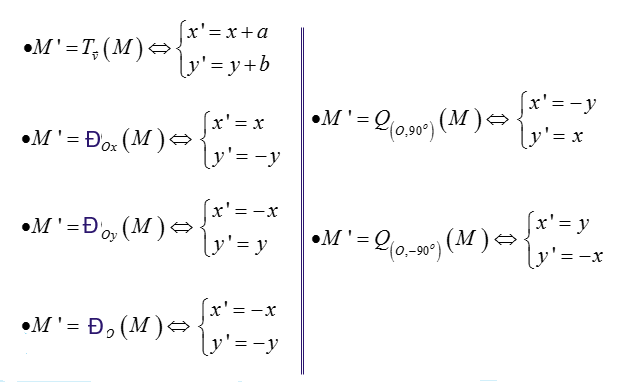
.png)