Câu hỏi trắc nghiệm (40 câu):
-
Câu 1: Mã câu hỏi: 410174
Điêu kiện có nghĩa của biểu thức \(\frac{x}{{\sqrt {x - 2} }} + \frac{{\sqrt {{x^2} + 1} }}{{x - 3}}\) là
- A. \({x \ne 3}\)
- B. \({x > 2}\)
- C. \(x\in\mathbb{R}\)
- D. \(\left\{ {\begin{array}{*{20}{l}} {x > 2}\\ {x \ne 3} \end{array}} \right.\)
-
Câu 2: Mã câu hỏi: 410175
\(\frac{{x + 1}}{{\sqrt {2 - x} }}\) có nghĩa khi :
- A. \( x \le 2\)
- B. \( x < 2\)
- C. \(x <- 2\)
- D. \(x \le- 2\)
-
Câu 3: Mã câu hỏi: 410176
Điều kiện có nghĩa của biểu thức \(\frac{{\sqrt {{x^2} + 2} }}{x}\) là:
- A. \(x > 0\)
- B. \( x \in \mathbb{R}\)
- C. x < 0
- D. \(x \ne 0\)
-
Câu 4: Mã câu hỏi: 410177
Tính giá trị biểu thức \(\sqrt {{{(2 - \sqrt 3 )}^2}} + \sqrt {{{(1 - \sqrt 3 )}^2}} \)
- A. 3
- B. 1
- C. \(2\sqrt 3 \)
- D. 2
-
Câu 5: Mã câu hỏi: 410178
So sánh hai số 2 và \(1 + \sqrt 2
- A. 2 ≥ \(1 + \sqrt 2 \)
- B. 2 = 1 + \sqrt 2
- C. \(2<1 + \sqrt 2 \)
- D. Không thể so sánh
-
Câu 6: Mã câu hỏi: 410179
Cho tam giác có độ dài các cạnh là 5,12,13. Tìm góc đối diện với cạnh có độ dài 13 của tam giác.
- A. Góc nhọn
- B. Góc vuông
- C. Góc tù
- D. Góc bẹt
-
Câu 7: Mã câu hỏi: 410185
Tính x và y trong hình:
- A. \(x=5;5\sqrt 2 \)
- B. \(x=5;\sqrt 2 \)
- C. \(x=3;5\sqrt 2 \)
- D. \(x=3;\sqrt 2 \)
-
Câu 8: Mã câu hỏi: 410189
Cho tam giác ABC vuông tại A có đường cao AH, cho CH = 16cm, CB = 21cm. Độ dài của AC gần đúng với kết quả nào sau đây?
- A. 21,2cm
- B. 13,5cm
- C. 12cm
- D. 18,3cm
-
Câu 9: Mã câu hỏi: 410191
Tìm x: \( \sqrt {4{x^2} + 4x + 1} = 5\)
- A. x=−3,x=−2
- B. x=3,x=2
- C. x=−3,x=2
- D. x=3,x=−2
-
Câu 10: Mã câu hỏi: 410192
Tập hợp các số thực x để \(\begin{aligned} &\frac{(\sqrt{x}-1)\left(x^{2}-4\right)}{(x-1)}=0 \end{aligned}\) là
- A. x = 1
- B. x = 2
- C. x = -2
- D. x = 3
-
Câu 11: Mã câu hỏi: 410193
Giá trị nhỏ nhất của biểu thức \(P=x+\sqrt{x}-1\) bằng
- A. \(P_{\min }=-1\)
- B. \(P_{\min }=0\)
- C. \(P_{\min }=1\)
- D. \(P_{\min }=-2\)
-
Câu 12: Mã câu hỏi: 410195
Biểu thức \(P=\sqrt{x-1}+\sqrt{3-x}\) có nghĩa khi
- A. \(1 \leq x \leq 3\)
- B. \( x \leq 3\)
- C. \(1< x \leq 3\)
- D. \( x \geq 3\)
-
Câu 13: Mã câu hỏi: 410197
Rút gọn biểu thức \(\sqrt {11 + 6\sqrt 2 } - 3 + \sqrt 2 \)
- A. \(\sqrt 2 \)
- B. \(2\sqrt 2 \)
- C. \(3\sqrt 2 \)
- D. \(4\sqrt 2 \)
-
Câu 14: Mã câu hỏi: 410200
Tìm x, biết: \( \sqrt {4 - 5x} = 12\)
- A. -22
- B. -24
- C. -26
- D. -28
-
Câu 15: Mã câu hỏi: 410201
Tìm x, biết: \( \sqrt {2x - 1} = \sqrt 5 \)
- A. 1
- B. 3
- C. 4
- D. 2
-
Câu 16: Mã câu hỏi: 410203
Giá trị của \( \sqrt {1,6} .\sqrt {2,5} \) bằng:
- A. 0,20
- B. 2,0
- C. 20,0
- D. 0,02
-
Câu 17: Mã câu hỏi: 410205
Thu gọn \(\begin{aligned} &\sqrt {4{x^2} + 24x + 36} \end{aligned} \) với x<-3 ta được:
- A. \( 6\left( {x + 3} \right)\)
- B. \(- 6\left( {x + 3} \right)\)
- C. \(18\left( {x + 3} \right)\)
- D. \(- 18\left( {x + 3} \right)\)
-
Câu 18: Mã câu hỏi: 410207
Thu gọn \(\sqrt {4{x^2} + 12x + 9} \) ta được:
- A. \( {2x + 3} \)
- B. \( \left| {2x + 3} \right|\)
- C. \(- ({2x + 3} )\)
- D. \(2(2x+3)\)
-
Câu 19: Mã câu hỏi: 410209
Cho tam giác ABC vuông tại A có cạnh AB = 6cm và AC = 8cm. Các đường phân giác trong và ngoài của góc B cắt đường thẳng AC lần lượt tại M và N. Tính đoạn thẳng AM
- A. 2cm
- B. 3cm
- C. 4cm
- D. 1cm
-
Câu 20: Mã câu hỏi: 410211
Cho tam giác ABC vuông tại A có đường cao AH. Qua B vẽ đường thẳng vuông góc với BC cắt đường thẳng AC tại D. Tia phân giác của góc C cắt AB tại N và BD tại M. Chọn câu đúng
- A. CN.CB = CM.CD
- B. CN.CM = CD.CB
- C. CN2 = CM.CB
- D. CN.CD = CM.CB
-
Câu 21: Mã câu hỏi: 410217
Cho tam giác cân (ABC ) có đáy (BC = 2a ), cạnh bên bằng b( b > a). Tính diện tích tam gíac ABC
- A. \( S = a\sqrt {{b^2} - {a^2}} \)
- B. \( S = \frac{1}{2}a\sqrt {{b^2} - {a^2}} \)
- C. \( S = \frac{1}{2}\sqrt {{b^2} - {a^2}} \)
- D. \( S = \sqrt {{b^2} - {a^2}} \)
-
Câu 22: Mã câu hỏi: 410220
Tìm x thỏa mãn điều kiện: \( \frac{{\sqrt {4x + 3} }}{{\sqrt {x + 1} }} = 3\)
- A. 1,2
- B. -1,2
- C. 0
- D. Vô nghiệm
-
Câu 23: Mã câu hỏi: 410222
Tính: \( \sqrt {1\frac{9}{{16}}} \)
- A. \(\frac{3}{4}\)
- B. \(\frac{5}{4}\)
- C. \(\frac{7}{4}\)
- D. \(\frac{1}{4}\)
-
Câu 24: Mã câu hỏi: 410224
Rút gọn biểu thức \(A=\sqrt{\frac{4 x^{2} y^{4}}{64}}\) ta được
- A. \(\frac{x\cdot y^{2}}{4}\)
- B. \(\frac{|x| \cdot y^{2}}{4}\)
- C. \(\frac{x \cdot y^{2}}{2}\)
- D. \(\frac{xy}{4}\)
-
Câu 25: Mã câu hỏi: 410228
Rút gọn biểu thức \(\begin{aligned} A =3 x+\sqrt{16-24 x+9 x^{2}} \end{aligned}\) ta được
- A. \(3 x+|4-3 x|\)
- B. \(6x-4\)
- C. 4
- D. 1
-
Câu 26: Mã câu hỏi: 410239
Cho \(\sqrt{\frac{9}{16} \cdot x^{2} \cdot y^{6}}\). Đưa thừa số ra ngoài dấu căn ta được
- A. \(\frac{3}{4} x.y^3\)
- B. \(-\frac{3}{4} \cdot|x| \cdot\left|y^{3}\right|\)
- C. \(\frac{9}{4} .x.y^3\)
- D. \(\frac{3}{4} \cdot|x| \cdot\left|y^{3}\right|\)
-
Câu 27: Mã câu hỏi: 410240
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D và E lần lượt là hình chiếu vuông góc của H trên AB,AC. Chọn câu đúng.
- A. DE3=BD.CE.BC
- B. DE2=BD.CE.BC
- C. DE4=BD.CE.BC
- D. Cả A, B, C đều sai.
-
Câu 28: Mã câu hỏi: 410241
Cho tam giác ABC vuông tại A, kẻ đường cao AH . Biết AH = 12cm, BH = 9cm. Tính diện tích tam giác ABC
- A. 60cm2
- B. 72cm2
- C. 78cm2
- D. 79cm2
-
Câu 29: Mã câu hỏi: 410242
Cho tam giác ABC vuông tại A có AB = 3cm, AC = 4cm. Tính độ dài đường cao AH của tam giác ABC.
- A. \(AH = \frac{{12}}{7}\)
- B. \(AH = \frac{{5}}{2}\)
- C. \(AH = \frac{{12}}{5}\)
- D. \(AH = \frac{{7}}{2}\)
-
Câu 30: Mã câu hỏi: 410243
Một con mèo ở trên cành cây cao 6,5m. Để bắt mèo xuống cần phải đặt thang sao cho đầu thang đạt độ cao đó, khi đó góc của thang với mặt đất là bao nhiêu, biết chiếc thang dài 6,7m ?
- A. \(55^057′\)
- B. \(75^057′\)
- C. \(25^057′\)
- D. \(35^057′\)
-
Câu 31: Mã câu hỏi: 410244
Rút gọn các biểu thức: \( \sqrt {15 - 6\sqrt 6 } + \sqrt {33 - 12\sqrt 6 } \)
- A. \(\sqrt 6\)
- B. \(\sqrt 5\)
- C. 6
- D. \(\sqrt 8\)
-
Câu 32: Mã câu hỏi: 410246
Phương trình \(2\sqrt {x + 2 + 2\sqrt {x + 1} } - \sqrt {x + 1} = 4\) có nghiệm là:
- A. x = 5
- B. x = 2
- C. x = 3
- D. x = 7
-
Câu 33: Mã câu hỏi: 410248
Giá trị của biểu thức \(\left(\sqrt{\frac{49}{3}}-\sqrt{\frac{25}{3}}+\sqrt{3}\right) \cdot \sqrt{3}\) là:
- A. 1
- B. \(\sqrt 3\)
- C. 5
- D. 2
-
Câu 34: Mã câu hỏi: 410250
Cho \(A = \frac{{\sqrt {45} + \sqrt {20} }}{{\sqrt {180} - \sqrt {80} }}\). Tính 3 A
- A. \(\frac{15}{2}\)
- B. \(\frac{13}{2}\)
- C. \(\frac{1}{2}\)
- D. \(9\)
-
Câu 35: Mã câu hỏi: 410252
Mô tả cánh của một máy bay. Hãy tính các độ dài DB của cánh máy bay theo số liệu được cho trong hình đó.
.png)
- A. 5,5m
- B. 5,77m
- C. 4,5m
- D. 4,77m
-
Câu 36: Mã câu hỏi: 410254
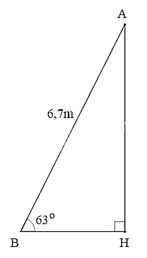
Thang AB dài 6,7m tựa vào tường làm thành góc 630 với mặt đất. Hỏi chiều cao của thang đạt được so với mặt đất ?
- A. 5m
- B. 4m
- C. 6m
- D. 7m
-
Câu 37: Mã câu hỏi: 410256
Tính: \( \frac{3}{{\sqrt 7 - 1}} - \frac{{\sqrt 7 - \sqrt {21} }}{{2 - 2\sqrt 3 }}\)
- A. \( \frac{1}{2}\)
- B. \(- \frac{1}{2}\)
- C. -1
- D. -2
-
Câu 38: Mã câu hỏi: 410258
Phương trình \(\sqrt {(2x - 8)(4 + x)} + 2\sqrt {(2x - 8)} = 0\) có nghiệm là:
- A. x = 1
- B. x = 3
- C. x = 5
- D. x = 4
-
Câu 39: Mã câu hỏi: 410260
Giải phương trình: \( \sqrt {{x^2} - 8x + 16} = 2\)
- A. S={2;6}
- B. S={-2;6}
- C. S={1;6}
- D. S={-1;6}
-
Câu 40: Mã câu hỏi: 410261
Tính tổng các nghiệm của phương trình \( \sqrt {3{x^2} - 3x - 4} = \sqrt {3x + 5}\)
- A. 2
- B. 3
- C. 1
- D. 0





.JPG)