YOMEDIA
NONE

  • Ta có y' = 3x2 - 4x + m

    Hàm số đạt cực trị tại x = 1 thì y'(1) => m = 1

    Với m = 1 thì hàm số đã cho trở thành y = x3 - 2x2 + x + 1

    Ta có y' = 3x2 - 4x + 1, y'' = 6x - 4 Vì y''(1) = 2 > nên hàm số đạt cực tiểu tại x = 1.

    Do vậy không có m thỏa mãn. Chọn đáp án D.

    Chú ý. Sai lầm có thể gặp phải: khi giải y'(1) = 0 => m = 1 đã vội kết luận mà không kiểm tra lại, dẫn đến chọn đáp án B.

    Câu hỏi:

    Cho tam giác ABC nội tiếp đường tròn tâm O, bán kính R, có \(\widehat {BAC} = {75^0};\,\,\widehat {ACB} = {60^0};\,\,BH \bot AC\). Quay tam giác ABC quanh AC thì tam giác BHC tạo thành hình nón tròn xoay (N). Tính diện tích xung quanh của hình nón đó theo R?

    • A. \(\frac{{3 + 2\sqrt 2 }}{2}\pi {R^2}\)
    • B. \(\frac{{3 + 2\sqrt 3 }}{2}\pi {R^2}\)   
    • C. \(\frac{{\sqrt 3 \left( {\sqrt 2  + 1} \right)}}{4}\pi {R^2}\)
    • D. \(\frac{{\sqrt 3 \left( {\sqrt 3  + 1} \right)}}{4}\pi {R^2}\)

    Đáp án đúng: B

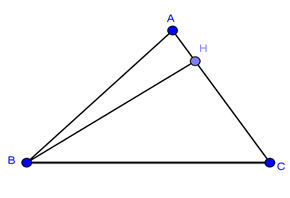
    Đặt BC = a, ta có: \(HC = \frac{a}{2};\,\,BH = \frac{{a\sqrt 3 }}{2}\)

    \(\cos {15^0} = \frac{{BH}}{{AB}} = \frac{{\sqrt 6  + \sqrt 2 }}{4}a \Rightarrow AB = \frac{{ - \sqrt 6  + 3\sqrt 2 }}{2}a;\,\,AH = \frac{{ - 3 + 2\sqrt 3 }}{2}a \Rightarrow AC = a\left( {\sqrt 3  - 1} \right)\)

    \(S = \frac{{abc}}{{4R}} = \frac{1}{2}\left( {\sqrt 3  - 1} \right){a^2}.\sin {60^0} = \frac{{\sqrt 3 }}{4}\left( {\sqrt 3  - 1} \right){a^2} = \frac{{{a^3}\left( {2\sqrt 6  - 3\sqrt 2 } \right)}}{{4R}} \Rightarrow R = a\frac{{\sqrt 6  - \sqrt 2 }}{2}\)

    \( \Rightarrow a = R.\frac{{\sqrt 6  + \sqrt 2 }}{2}\)

    \( \Rightarrow {S_{xq}} = \pi \frac{a}{2}.\frac{{a\sqrt 3 }}{2} = \pi \frac{{\sqrt 3 }}{4}.{\left( {\frac{{\sqrt 6  + \sqrt 2 }}{2}} \right)^2}.{R^2} = \pi {R^2}\frac{{3 + 2\sqrt 3 }}{2}.\)

    YOMEDIA
YOMEDIA

Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng

 

 

CÂU HỎI KHÁC VỀ MẶT NÓN, HÌNH NÓN, KHỐI NÓN

AANETWORK
 

XEM NHANH CHƯƠNG TRÌNH LỚP 12

 

YOMEDIA
ATNETWORK
ON