Cho hình thang cân ABCD có AB//CD. Gọi M, N lần lượt là trung điểm của AB, CD

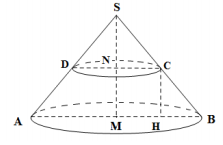
Kéo dài AD và BC cắt nhau tại S. Vì ABCD là hình thang cân nên tam giác SAB là tam giác cân. $\Rightarrow SM \bot AB,SN \bot CD \Rightarrow S,M,N$ thẳng hàng.

Quay tam giác vuông SAB quanh đường thẳng MN ta được khối nón tròn xoay có đỉnh S và đáy là hình tròn tâm M bán kính MA.

Thể tích khối tròn xoay có được khi quay hình thang ABCD quanh đường thẳng MN bằng hiệu thể tích của khối nón ${V_1}$ đỉnh S, đáy là hình tròn (M; MA) và thể tích khối nón ${V_2}$ đỉnh S, đáy là hình tròn (N; NC).

Ta thấy: $AB = 2.CD;\,\,AB//CD \Rightarrow CD$ là đường  trung bình của tam giác SAB.

$\Rightarrow$ N là trung điểm của SM.

Kẻ $CH \bot AB \Rightarrow CH = MN = \frac{{AB}}{4} = \frac{{MB}}{2} \Rightarrow CH = HB$

Xét tam giác CHB vuông tại H có: $CH = HB = \frac{{BC}}{{\sqrt 2 }} = a$

$\begin{array}{l} \Rightarrow MN = a \Rightarrow SM = 2MN = 2a;\,\,CN = NM = a;\,\,MB = 2.MN = 2a.\\{V_1} = \frac{\pi }{3}.M{B^2}.SM = \frac{{8\pi }}{3}.{a^3};{V_2} = \frac{\pi }{3}.N{C^2}.SN = \frac{\pi }{3}{a^3}.\\ \Rightarrow V = {V_1} - {V_2} = \frac{{7\pi }}{3}.{a^3}\end{array}$