YOMEDIA
NONE

  • \(P = \frac{1}{{16}} + 1 - \frac{1}{{\sqrt {64} }} - \frac{1}{{{{\left( {{{\left( { - 2} \right)}^5}} \right)}^{\frac{4}{5}}}}} = \frac{1}{{16}} + 1 - \frac{1}{8} - \frac{1}{{16}} = \frac{7}{8}\)

    Câu hỏi:

    Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và khoảng cách từ tâm của đáy đến một mặt bên bằng \(\frac{{a\sqrt 5 }}{5}.\) Tính diện tích toàn phần \({S_{tp}}\) của hình nón có đỉnh S và đáy là hình tròn ngoại tiếp tứ giác ABCD.

    • A. \({S_{tp}} = \frac{{\pi \left( {3 - \sqrt 2 } \right){a^2}}}{2}.\)
    • B. \({S_{tp}} = \frac{{\pi \left( {3 + \sqrt 2 } \right){a^2}}}{2}.\)
    • C. \({S_{tp}} = \frac{{\pi \left( {2 + \sqrt 3 } \right){a^2}}}{2}.\)
    • D.  \({S_{tp}} = \frac{{\pi \left( {1 + \sqrt 3 } \right){a^2}}}{2}.\)

    Đáp án đúng: D

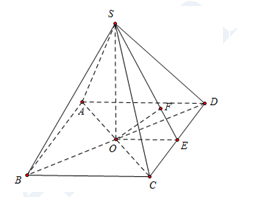
    Dựng \(\left\{ \begin{array}{l}OE \bot CD\\OF \bot SE\end{array} \right. \Rightarrow OF \bot \left( {SCD} \right).\)

    Ta có: \(\frac{1}{{O{F^2}}} = \frac{1}{{O{E^2}}} + \frac{1}{{S{O^2}}} \Rightarrow SO = a\)

    \( \Rightarrow {l_N} = SD = \sqrt {S{O^2} + O{D^2}}  = \frac{{a\sqrt 3 }}{{\sqrt 2 }}.\)

    \({R_d} = OD = \frac{a}{{\sqrt 2 }} \Rightarrow {S_{tp}} = \pi {r^2} + \pi rl = \frac{{\pi \left( {1 + \sqrt 3 } \right){a^2}}}{2}.\)

    YOMEDIA
YOMEDIA

Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng

 

 

CÂU HỎI KHÁC VỀ MẶT NÓN, HÌNH NÓN, KHỐI NÓN

AANETWORK
 

XEM NHANH CHƯƠNG TRÌNH LỚP 12

 

YOMEDIA
ATNETWORK
ON