Bạn có một cốc thủy tinh hình trụ, đường kính trong lòng đáy cốc là 6 cm chiều cao trong lòng cốc là 10 cm đang đựng một lượng nước. Bạn A nghiêng cốc nước, vừa lúc khi nước chạm miệng cốc thì ở đáy mực nước trùng với đường kính đáy

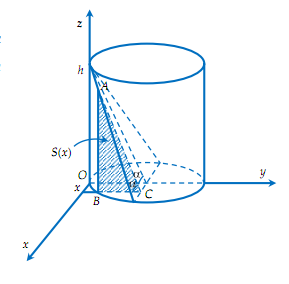
Chọn hệ trục tọa độ như hình vẽ.

Gọi S(x) là thiết diện của mặt phẳng vuông góc với trục Ox tại x.

Như hình vẽ ta thấy thiết liện này là tam giá vuông ABC.

Mặt khác:

\(\begin{array}{l}AB = BC.\tan \alpha  = \sqrt {{R^2} - {x^2}} .\tan \alpha \\ \Rightarrow {S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}\left( {{R^2} - {x^2}} \right).\tan \alpha \\ \Rightarrow V = \frac{1}{2}\int\limits_{ - 3}^3 {({3^2} - {x^2}).\frac{h}{R}dx = } \frac{1}{2}.\frac{{10}}{3}\int\limits_{ - 3}^3 {({3^2} - {x^2})dx = 60\,(c{m^3}).} \end{array}\)