Vß╗øi mong muß╗æn gi├║p c├Īc em hß╗Źc sinh dß╗ģ d├Āng hŲĪn trong viß╗ćc hß╗Źc tß║Łp m├┤n Vß║Łt l├Į, c┼®ng nhŲ░ dß╗ģ d├Āng chinh phß╗źc ─æŲ░ß╗Żc nhß╗»ng con ─æiß╗ām 9, ─æiß╗ām 10 , nhß╗»ng b├Āi tß║Łp ─æ├▓i hß╗Åi phß║Żi vß║Łn dß╗źng cao. Hß╗īC247 xin giß╗øi thiß╗ću tß╗øi c├Īc em T├Āi liß╗ću PhŲ░ŲĪng ph├Īp giß║Żi b├Āi to├Īn vß╗ü cß║»t gh├®p l├▓ xo m├┤n Vß║Łt L├Į 12 n─ām 2021-2022. Mß╗Øi c├Īc em c├╣ng tham khß║Żo v├Ā luyß╗ćn tß║Łp tß╗æt. Ch├║c c├Īc em hß╗Źc tß╗æt!
1. PHŲ»ŲĀNG PH├üP GIß║óI
Ta cß║¦n ch├║ ├Į mß╗Öt sß╗æ kiß║┐n thß╗®c sau:
* Cắt lò xo:
Giß║Ż sß╗Ł ta c├│ mß╗Öt l├▓ xo c├│ chiß╗üu d├Āi \({{l}_{0}}\) c├│ ─æß╗Ö cß╗®ng \({{k}_{0}}\). Cß║»t l├▓ xo n├Āy th├Ānh n ─æoß║Īn c├│ chiß╗üu d├Āi v├Ā ─æß╗Ö cß╗®ng lß║¦n lŲ░ß╗Żt l├Ā \({{k}_{1}},{{k}_{2}},...{{k}_{n}}.\) Khi ─æ├│ ta lu├┤n c├│
\({{k}_{0}}{{l}_{0}}={{k}_{1}}{{l}_{1}}={{k}_{2}}{{l}_{2}}=...={{k}_{n}}{{l}_{n}}=ES\)
* Gh├®p l├▓ xo
1.1. TrŲ░ß╗Øng hß╗Żp gh├®p nß╗æi tiß║┐p
2 l├▓ xo gh├®p nß╗æi tiß║┐p th├¼ ─æß╗Ö cß╗®ng cß╗¦a hß╗ć l├▓ xo (─æß╗Ö cß╗®ng tŲ░ŲĪng ─æŲ░ŲĪng):
\(\frac{1}{k}=\frac{1}{{{k}_{1}}}+\frac{1}{{{k}_{2}}}\Rightarrow k=\frac{{{k}_{1}}{{k}_{2}}}{{{k}_{1}}+{{k}_{2}}}\)
.jpg?enablejsapi=1)
Chß╗®ng minh:
X├®t khi vß║Łt ß╗¤ vß╗ŗ tr├Ł c├Īch vß╗ŗ tr├Ł c├ón bß║▒ng (l├▓ xo kh├┤ng biß║┐n dß║Īng) mß╗Öt ─æoß║Īn x. ─Éß╗Ö biß║┐n dß║Īng v├Ā lß╗▒c ─æ├Ān hß╗ōi cß╗¦a c├Īc l├▓ xo th├Ānh phß║¦n l├Ā \({{x}_{1}},{{x}_{2}},{{F}_{1}},{{F}_{2}}.\) Tß║Īi ─æiß╗ām nß╗æi giß╗»a hai l├▓ xo lß╗▒c ─æ├Ān hß╗ōi do l├▓ xo 1 t├Īc dß╗źng l├¬n l├▓ xo 2 tß║Īi ─æiß╗ām nß╗æi bß║▒ng vß╗øi lß╗▒c ─æ├Ān hß╗ōi do l├▓ xo 2 t├Īc dß╗źng l├¬n l├▓ xo do 1 tß║Īi ─æiß╗ām nß╗æi, tß╗®c l├Ā ta c├│
\({{F}_{1}}={{F}_{2}}\).
Gß╗Źi ─æß╗Ö biß║┐n dß║Īng v├Ā lß╗▒c ─æ├Ān hß╗ōi cß╗¦a l├▓ xo tŲ░ŲĪng ─æŲ░ŲĪng l├Ā \(x,F.\) Ta c├│
\(\begin{array}{l} \left\{ \begin{array}{l} F = {F_1} = {F_2}\\ x = {x_1} + {x_2} \end{array} \right. \Rightarrow \left\{ \begin{array}{l} F = - kx = - {k_1}{x_1} = - {k_2}{x_2}\\ x = {x_1} + {x_2} \end{array} \right.\\ \Rightarrow \frac{F}{{ - k}} = \frac{F}{{ - {k_1}}} + \frac{F}{{ - {k_2}}} \Rightarrow \frac{1}{k} = \frac{1}{{{k_1}}} + \frac{1}{{{k_2}}} \Rightarrow k = \frac{{{k_1}{k_2}}}{{{k_1} + {k_2}}} \end{array}\)
1.2. TrŲ░ß╗Øng hß╗Żp gh├®p song song
Khi 2 l├▓ xo c├│ ─æß╗Ö cß╗®ng \({{k}_{1}},{{k}_{2}}\) gh├®p song song th├¼ ─æß╗Ö cß╗®ng cß╗¦a hß╗ć l├▓ xo (─æß╗Ö cß╗®ng tŲ░ŲĪng ─æŲ░ŲĪng) ─æŲ░ß╗Żc x├Īc ─æß╗ŗnh bß╗¤i \(k={{k}_{1}}+{{k}_{2}}\).
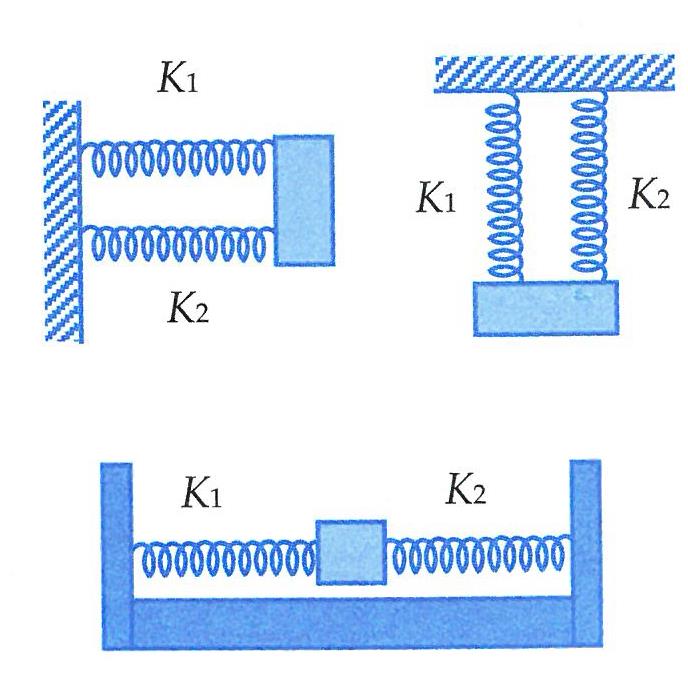
Chß╗®ng minh:
X├®t khi vß║Łt ß╗¤ vß╗ŗ tr├Ł c├Īch vß╗ŗ tr├Ł c├ón bß║▒ng (vß╗ŗ tr├Ł c├ón bß║▒ng chß╗Źn l├Ā vß╗ŗ tr├Ł l├▓ xo kh├┤ng biß║┐n dß║Īng) mß╗Öt ─æoß║Īn x. ─æß╗Ö biß║┐n dß║Īng v├Ā lß╗▒c ─æ├Ān hß╗ōi cß╗¦a c├Īc l├▓ xo th├Ānh phß║¦n l├Ā \({{x}_{1}},{{x}_{2}},{{F}_{1}},{{F}_{2}}.\)
─Éß╗Ö biß║┐n dß║Īng v├Ā lß╗▒c ─æ├Ān hß╗ōi cß╗¦a l├▓ xo tŲ░ŲĪng ─æŲ░ŲĪng l├Ā \(x,F.\) Ta c├│
\(\left\{ \begin{array}{l} F = {F_1} + {F_2}\\ x = {x_1} = {x_2} \end{array} \right. \Rightarrow \left\{ \begin{array}{l} - kx = - {k_1}{x_1} - {k_2}{x_2}\\ x = {x_1} = {x_2} \end{array} \right. \Rightarrow k = {k_1} + {k_2}\)
2. V├Ź Dß╗ż MINH Hß╗īA
V├Ł dß╗ź 1: Mß╗Öt l├▓ xo c├│ ─æß╗Ö d├Āi l = 50 cm, ─æß╗Ö cß╗®ng k = 50 N/m. Cß║»t l├▓ xo l├Ām 2 phß║¦n c├│ chiß╗üu d├Āi lß║¦n lŲ░ß╗Żt l├Ā \({{l}_{1}}\)= 20 cm, \({{l}_{2}}\)= 30 cm. T├¼m ─æß╗Ö cß╗®ng cß╗¦a mß╗Śi ─æoß║Īn
A. 150 N/m; 83,3 N/m.
B. 125 N/m; 133,3 N/m.
C. 150 N/m; 135,3 N/m.
D. 125 N/m; 83,33 N/m.
HŲ░ß╗øng dß║½n giß║Żi
Ta c├│
\({{k}_{0}}{{l}_{0}}={{k}_{1}}{{l}_{1}}={{k}_{2}}{{l}_{2}}\Rightarrow \left\{ \begin{align} & {{k}_{1}}=\frac{{{k}_{0}}{{l}_{0}}}{{{l}_{1}}}=\frac{50.50}{20}=125{N}/{m}\; \\ & {{k}_{2}}=\frac{{{k}_{0}}{{l}_{0}}}{{{l}_{2}}}=\frac{50.50}{30}=83,33{N}/{m}\; \\ \end{align} \right.\)
─É├Īp ├Īn D.
V├Ł dß╗ź 2: Mß╗Öt vß║Łt c├│ khß╗æi lŲ░ß╗Żng m gß║»n v├Āo l├▓ xo 1 c├│ ─æß╗Ö cß╗®ng \({{k}_{1}}\) th├¼ vß║Łt dao ─æß╗Öng ─æiß╗üu h├▓a vß╗øi chu k├¼ \({{T}_{1}}\), gß║»n vß║Łt ─æ├│ v├Āo l├▓ xo 2 c├│ ─æß╗Ö cß╗®ng \({{k}_{2}}\) th├¼ vß║Łt dao ─æß╗Öng ─æiß╗üu h├▓a vß╗øi chu k├¼ \({{T}_{2}}\). Khi gß║»n vß║Łt m v├Āo 2 l├▓ xo tr├¬n gh├®p nß╗æ├Ł tiß║┐p th├¼ chu k├¼, tß║¦n sß╗æ dao ─æß╗Öng cß╗¦a vß║Łt ─æŲ░ß╗Żc x├Īc ─æß╗ŗnh bß╗¤i biß╗āu thß╗®c n├Āo?
HŲ░ß╗øng dß║½n giß║Żi
V├¼ hß╗ć l├▓ xo gh├®p nß╗æi tiß║┐p n├¬n ─æß╗Ö cß╗®ng tŲ░ŲĪng ─æŲ░ŲĪng l├Ā \(\frac{1}{k}=\frac{1}{{{k}_{1}}}+\frac{1}{{{k}_{2}}}\)(1)
Mß║Ęt kh├Īc, ta c├│ \(T=2\pi \sqrt{\frac{m}{k}}\Rightarrow \frac{1}{k}=\frac{1}{4{{\pi }^{2}}m}.{{T}^{2}}\)
Tß╗®c l├Ā \(\frac{1}{k}\) tß╗ē lß╗ć thuß║Łn vß╗øi \({{T}^{2}}\), n├¬n kß║┐t hß╗Żp vß╗øi (1) ta ─æŲ░ß╗Żc \({{T}^{2}}={{T}_{1}}^{2}+{{T}_{2}}^{2}\)
Suy ra tß║¦n sß╗æ dao ─æß╗Öng ─æŲ░ß╗Żc x├Īc ─æß╗ŗnh bß╗¤i biß╗āu thß╗®c \(\frac{1}{{{f}^{2}}}=\frac{1}{{{f}_{1}}^{2}}+\frac{1}{{{f}_{2}}^{2}}\).
V├Ł dß╗ź 3: Mß╗Öt vß║Łt c├│ khß╗æi lŲ░ß╗Żng m gß║»n v├Āo l├▓ xo 1 c├│ ─æß╗Ö cß╗®ng \({{k}_{1}}\) th├¼ vß║Łt dao ─æß╗Öng ─æiß╗üu h├▓a vß╗øi chu k├¼ \({{T}_{1}}\), gß║»n vß║Łt ─æ├│ v├Āo l├▓ xo 2 c├│ ─æß╗Ö cß╗®ng \({{k}_{2}}\) th├¼ vß║Łt dao ─æß╗Öng ─æiß╗üu h├▓a vß╗øi chu k├¼ \({{T}_{2}}\). Khi gß║»n vß║Łt m v├Āo 2 l├▓ xo tr├¬n gh├®p song song th├¼ chu k├¼, tß║¦n sß╗æ dao ─æß╗Öng cß╗¦a vß║Łt ─æŲ░ß╗Żc x├Īc ─æß╗ŗnh bß╗¤i biß╗āu thß╗®c n├Āo?
HŲ░ß╗øng dß║½n giß║Żi
V├¼ hß╗ć l├▓ xo gh├®p nß╗æi tiß║┐p n├¬n ─æß╗Ö cß╗®ng tŲ░ŲĪng ─æŲ░ŲĪng l├Ā \(k={{k}_{1}}+{{k}_{2}}\)(2)
Mß║Ęt kh├Īc, ta c├│ \(T=2\pi \sqrt{\frac{m}{k}}\Rightarrow \frac{1}{k}=\frac{1}{4{{\pi }^{2}}m}.{{T}^{2}}\)
Tß╗®c l├Ā \(\frac{1}{k}\) tß╗ē lß╗ć thuß║Łn vß╗øi \({{T}^{2}}\), n├¬n kß║┐t hß╗Żp vß╗øi (1) ta ─æŲ░ß╗Żc \(\frac{1}{{{T}^{2}}}=\frac{1}{{{T}_{1}}^{2}}+\frac{1}{{{T}_{2}}^{2}}\).
Suy ra tß║¦n sß╗æ dao ─æß╗Öng ─æŲ░ß╗Żc x├Īc ─æß╗ŗnh bß╗¤i biß╗āu thß╗®c \({{f}^{2}}={{f}_{1}}^{2}+{{f}_{2}}^{2}\)
V├Ł dß╗ź 4: Mß╗Öt con lß║»c l├▓ xo khi gß║»n vß║Łt m vß╗øi l├▓ xo \({{k}_{1}}\)th├¼ chu k├¼ l├Ā \({{T}_{1}}\)= 3s. Nß║┐u gß║»n vß║Łt m ─æ├│ v├Āo l├▓ xo \({{k}_{2}}\) th├¼ dao ─æß╗Öng vß╗øi chu k├¼ \({{T}_{2}}\)= 4s. Tm chu k├¼ cß╗¦a con lß║»c l├▓ xo ß╗®ng vß╗øi c├Īc trŲ░ß╗Øng hß╗Żp gh├®p nß╗æi tiß║┐p v├Ā song song hai l├▓ xo vß╗øi nhau
A. 5s; 1s. B. 6s; 4s. C. 5s; 2,4s. D. 10s; 7s.
HŲ░ß╗øng dß║½n giß║Żi
Khi hai lò xo mắc nối tiếp ta có \(T=\sqrt{{{T}_{1}}^{2}+{{T}_{2}}^{2}}=\sqrt{{{3}^{2}}+{{4}^{2}}}=5.\)
Khi hai l├▓ xo gh├®p song song ta c├│ \(T=\frac{{{T}_{1}}.{{T}_{2}}}{\sqrt{{{T}_{1}}^{2}+{{T}_{2}}^{2}}}=\frac{3.4}{\sqrt{{{3}^{2}}+{{4}^{2}}}}=2,4.\)
─É├Īp ├Īn C.
V├Ł dß╗ź 5: Mß╗Öt l├▓ xo c├│ ─æß╗Ö d├Āi \({{l}_{0}}\), ─æß╗Ö cß╗®ng \({{k}_{0}}\)= 100 N/m. Cß║»t l├▓ xo l├Ām 3 ─æoß║Īn tß╗ē lß╗ć 1:2:3. X├Īc ─æß╗ŗnh ─æß╗Ö cß╗®ng cß╗¦a mß╗Śi ─æoß║Īn.
A. 200; 400; 600 N/m.
B. 100; 300; 500 N/m.
C. 200; 300; 400 N/m.
D. 200; 300; 600 N/m.
HŲ░ß╗øng dß║½n giß║Żi
Ta c├│ khi cß║»t l├▓ xo th├¼ t├Łch cß╗¦a ─æß╗Ö cß╗®ng v├Ā chiß╗üu d├Āi l├Ā kh├┤ng ─æß╗Ģi
\({{k}_{0}}.{{l}_{0}}={{k}_{1}}.{{l}_{1}}={{k}_{2}}.{{l}_{2}}={{k}_{3}}.{{l}_{3}}\)
V├¼ ta cß║»t l├▓ xo l├Ām 3 ─æoß║Īn c├│ tß╗ē lß╗ć 1:2:3 n├¬n ta c├│:
\(\frac{{{l}_{1}}}{1}=\frac{{{l}_{2}}}{2}=\frac{{{l}_{3}}}{3}\Rightarrow \frac{{{l}_{1}}}{1}=\frac{{{l}_{2}}}{2}=\frac{{{l}_{3}}}{3}=\frac{{{l}_{1}}+{{l}_{2}}+{{l}_{3}}}{1+2+3}=\frac{{{l}_{0}}}{6}\Rightarrow \left\{ \begin{align} & {{l}_{1}}=\frac{{{l}_{0}}}{6} \\ & {{l}_{2}}=\frac{{{l}_{0}}}{3} \\ & {{l}_{3}}=\frac{{{l}_{0}}}{2} \\ \end{align} \right.\)
NhŲ░ vß║Ły ─æß╗Ö cß╗®ng cß╗¦a l├▓ xo thß╗® nhß║źt l├Ā
\(\left\{ \begin{align} & {{k}_{1}}=\frac{{{k}_{0}}{{l}_{0}}}{{{l}_{1}}} \\ & {{l}_{1}}=\frac{{{l}_{0}}}{6} \\ & {{k}_{0}}=100{N}/{m}\; \\ \end{align} \right.\Rightarrow {{k}_{1}}=100.6=600{N}/{m}\;\)
TŲ░ŲĪng tß╗▒ ta t├Łnh ─æŲ░ß╗Żc \({{k}_{2}}\)= 300 N/m v├Ā \({{k}_{3}}\)= 200 N/m.
─É├Īp ├Īn D.
V├Ł dß╗ź 6: L├▓ xo thß╗® nhß║źt c├│ ─æß╗Ö cß╗®ng \({{K}_{1}}\)= 400 N/m, l├▓ xo thß╗® hai c├│ ─æß╗Ö cß╗®ng l├Ā \({{K}_{2}}\)= 600 N/m. Hß╗Åi nß║┐u gh├®p song song hai l├▓ xo tr├¬n th├¼ ─æß╗Ö cß╗®ng l├Ā bao nhi├¬u?
A. 600 N/m.
B. 500 N/m.
C. 1000 N/m.
D. 2400 N/m.
HŲ░ß╗øng dß║½n giß║Żi
V├¼ hai l├▓ xo gh├®p song song n├¬n c├│ ─æß╗Ö cß╗®ng tŲ░ŲĪng ─æŲ░ŲĪng l├Ā
\(\Rightarrow k={{k}_{1}}+{{k}_{2}}\)= 400 + 600 = 1000 N/m \(\)
─É├Īp ├Īn C.
V├Ł dß╗ź 7: L├▓ xo 1 c├│ ─æß╗Ö cß╗®ng \({{k}_{1}}\)= 400 N/m, l├▓ xo 2 c├│ ─æß╗Ö cß╗®ng l├Ā \({{k}_{2}}\)= 600 N/m. Hß╗Åi nß║┐u gh├®p nß╗æi tiß║┐p 2 l├▓ xo tr├¬n th├¼ ─æß╗Ö cß╗®ng cß╗¦a hß╗ć l├Ā bao nhi├¬u?
A. 600 N/m. B. 500 N/m. C. 1000 N/m. D. 240 N/m.
HŲ░ß╗øng dß║½n giß║Żi
V├¼ 2 l├▓ xo mß║»c nß╗æi tiß║┐p n├¬n ta c├│ ─æß╗Ö cß╗®ng tŲ░ŲĪng ─æŲ░ŲĪng l├Ā
\(k=\frac{{{k}_{1}}{{k}_{2}}}{{{k}_{1}}+{{k}_{2}}}=\frac{400.600}{400+600}=240\)(N/m)
─É├Īp ├Īn D.
V├Ł dß╗ź 8: Mß╗Öt l├▓ xo ─æß╗ōng chß║źt, tiß║┐t diß╗ćn ─æß╗üu ─æŲ░ß╗Żc cß║»t th├Ānh ba l├▓ xo c├│ chiß╗üu d├Āi tß╗▒ nhi├¬n l├Ā \(l\),(cm), (\(l\)-10) (cm) v├Ā (\(l\)- 20) (cm). Lß║¦n lŲ░ß╗Żt gß║»n mß╗Śi l├▓ xo n├Āy (theo thß╗® tß╗▒ tr├¬n) vß╗øi vß║Łt nhß╗Å khß╗æi lŲ░ß╗Żng m th├¼ ─æŲ░ß╗Żc ba con lß║»c c├│ chu k├¼ dao ─æß╗Öng ri├¬ng tŲ░ŲĪng ß╗®ng l├Ā 2s, \(\sqrt{3}\)s v├Ā T. Biß║┐t ─æß╗Ö cß╗®ng cß╗¦a c├Īc l├▓ xo tß╗ē lß╗ć nghß╗ŗch vß╗øi chiß╗üu d├Āi tß╗▒ nhi├¬n cß╗¦a n├│. Gi├Ī trß╗ŗ cß╗¦a T l├Ā
A. 1,00 s. B. 1,28 s. C. 1,41 s. D. 1,50 s.
HŲ░ß╗øng dß║½n giß║Żi
V├¼ ─æß╗Ö cß╗®ng l├▓ xo tß╗ē lß╗ć nghß╗ŗch vß╗øi chiß╗üu d├Āi tß╗▒ nhi├¬n, n├¬n ta c├│:
\(\begin{array}{l} \left\{ \begin{array}{l} \frac{{{T_1}}}{{{T_2}}} = \sqrt {\frac{{{k_2}}}{{{k_1}}}} = \sqrt {\frac{{{l_1}}}{{{l_2}}}} \\ \frac{{{T_1}}}{{{T_3}}} = \sqrt {\frac{{{l_1}}}{{{l_3}}}} \end{array} \right. \Rightarrow \left\{ \begin{array}{l} \frac{2}{{\sqrt 3 }} = \sqrt {\frac{l}{{l - 10}}} \\ \frac{2}{T} = \sqrt {\frac{l}{{l - 20}}} \end{array} \right. \Rightarrow \left\{ \begin{array}{l} l = 40\\ T = \frac{2}{{\sqrt {l - 20} }} \end{array} \right. \Rightarrow T = \sqrt 2 \left( s \right).\\ \end{array}\)
─É├Īp ├Īn C.
3. B├ĆI Tß║¼P Tß╗░ LUYß╗åN
C├óu 1: Mß╗Öt con lß║»c l├▓ xo gß╗ōm vß║Łt nß║Ęng m treo dŲ░ß╗øi l├▓ xo d├Āi. Chu kß╗│ dao ─æß╗Öng l├Ā T. Chu kß╗│ dao ─æß╗Öng l├Ā bao nhi├¬u nß║┐u giß║Żm ─æß╗Ö d├Āi l├▓ xo xuß╗æng 2 lß║¦n:
A. \({T}'=\frac{T}{2}.\)
B. \({T}'=2T.\)
C. \({T}'=T\sqrt{2}.\)
D. \({T}'=\frac{T}{\sqrt{2}}.\)
C├óu 2: Mß╗Öt con lß║»c l├▓ xo gß╗ōm vß║Łt nß║Ęng m treo dŲ░ß╗øi l├▓ xo d├Āi. Chu kß╗│ dao ─æß╗Öng l├Ā T. Chu kß╗│ dao ─æß╗Öng l├Ā bao nhi├¬u nß║┐u t─āng ─æß╗Ö d├Āi l├▓ xo l├¬n 2 lß║¦n:
A. \({T}'=\frac{T}{2}.\)
B. \({T}'=2T.\)
C. \({T}'=T\sqrt{2}.\)
D. \({T}'=\frac{T}{\sqrt{2}}.\)
C├óu 3: C├│ n l├▓ xo khi treo c├╣ng mß╗Öt vß║Łt nß║Ęng v├Āo mß╗Śi l├▓ xo th├¼ chu k├¼ dao ─æß╗Öng tŲ░ŲĪng ß╗®ng cß╗¦a mß╗Śi l├▓ xo l├Ā \({{T}_{1}},{{T}_{2}},...{{T}_{n}}\) nß║┐u mß║»c nß╗æi tiß║┐p n l├▓ xo tr├¬n rß╗ōi treo c├╣ng mß╗Öt vß║Łt nß║Ęng th├¼ chu kß╗│ hß╗ć l├Ā:
A. \({{T}^{2}}=T_{1}^{2}+T_{2}^{2}+...+T_{n}^{2}.\)
B. \(T={{T}_{1}}+{{T}_{2}}+...+{{T}_{n}}.\)
C. \(\frac{1}{{{T}_{2}}}=\frac{1}{T_{1}^{2}}+\frac{1}{T_{2}^{2}}+...+\frac{1}{T_{n}^{2}}.\)
D. \(\frac{1}{T}=\frac{1}{{{T}_{1}}}+\frac{1}{{{T}_{2}}}+...+\frac{1}{{{T}_{n}}}.\)
C├óu 4: C├│ n l├▓ xo khi treo c├╣ng mß╗Öt vß║Łt nß║Ęng v├Āo mß╗Śi l├▓ xo th├¼ chu k├¼ dao ─æß╗Öng tŲ░ŲĪng ß╗®ng cß╗¦a mß╗Śi l├▓ xo l├Ā \({{T}_{1}},{{T}_{2}},...{{T}_{n}}\) nß║┐u gh├®p song song n l├▓ xo tr├¬n rß╗ōi treo c├╣ng mß╗Öt vß║Łt nß║Ęng th├¼ chu k├¼ hß╗ć l├Ā:
A. \({{T}^{2}}=T_{1}^{2}+T_{2}^{2}+...+T_{n}^{2}.\)
B. \(T={{T}_{1}}+{{T}_{2}}+...+{{T}_{n}}.\)
C. \(\frac{1}{{{T}_{2}}}=\frac{1}{T_{1}^{2}}+\frac{1}{T_{2}^{2}}+...+\frac{1}{T_{n}^{2}}.\)
D. \(\frac{1}{T}=\frac{1}{{{T}_{1}}}+\frac{1}{{{T}_{2}}}+...+\frac{1}{{{T}_{n}}}.\)
C├óu 5: Mß╗Öt con lß║»c l├▓ xo c├│ ─æß╗Ö d├Āi tß╗▒ nhi├¬n \({{l}_{0}}\), ─æß╗Ö cß╗®ng l├Ā \({{k}_{0}}=50{N}/{m}\;\). Nß║┐u cß║»t l├▓ xo l├Ām 4 ─æoß║Īn vß╗øi tß╗ē lß╗ć 1:2:3:4 th├¼ ─æß╗Ö cß╗®ng cß╗¦a mß╗Śi ─æoß║Īn l├Ā bao nhi├¬u?
A. 500; 400; 300; 200.
B. 500; 250; 166,67; 125.
C. 500; 166,7; 125; 250.
D. 500; 250; 450; 230.
C├óu 6: C├│ hai l├▓ xo \({{K}_{1}}=50{N}/{m}\;\) v├Ā \({{K}_{2}}=60{N}/{m}\;\). Gß║»n nß╗æi tiß║┐p hai l├▓ xo tr├¬n v├Āo vß║Łt \(m=0,4\,\,kg\). T├¼m chu kß╗│ dao ─æß╗Öng cß╗¦a hß╗ć?
A. 0,760 s.
B. 0,789 s.
C. 0,350 s.
D. 0,379 s.
C├óu 7: Gß║»n vß║Łt m v├Āo l├▓ xo \({{K}_{1}}\) th├¼ vß║Łt dao ─æß╗Öng vß╗øi tß║¦n sß╗æ \({{f}_{1}}\); gß║»n vß║Łt m v├Āo l├▓ xo \({{K}_{2}}\) th├¼ n├│ dao ─æß╗Öng vß╗øi tß║¦n sß╗æ \({{f}_{2}}\). Hß╗Åi nß║┐u gß║»n vß║Łt m v├Āo l├▓ xo c├│ ─æß╗Ö cß╗®ng \(K=2{{K}_{1}}+3{{K}_{2}}\) th├¼ tß║¦n sß╗æ sß║Į l├Ā bao nhi├¬u?
A. \(f=\sqrt{f_{1}^{2}+f_{2}^{2}}.\)
B. \(f=2{{f}_{1}}+3{{f}_{2}}.\)
C. \(f=\sqrt{2f_{1}^{2}+3f_{2}^{2}}.\)
D. \(f=6{{f}_{1}}.{{f}_{2}}.\)
C├óu 8: Gß║»n vß║Łt m v├Āo l├▓ xo \({{K}_{1}}\) th├¼ vß║Łt dao ─æß╗Öng vß╗øi chu kß╗│ \({{T}_{1}}=0,3\text{s}\), gß║»n vß║Łt m v├Āo l├▓ xo \({{K}_{2}}\) th├¼ dao ─æß╗Öng vß╗øi chu kß╗│ \({{T}_{2}}=0,4\text{s}\). Hß╗Åi nß║┐u gß║»n vß║Łt m v├Āo l├▓ xo \({{K}_{1}}\) song song \({{K}_{2}}\) th├¼ chu kß╗│ cß╗¦a hß╗ć l├Ā?
A. 0,20 s.
B. 0,17 s.
C. 0,50 s.
D. 0,24 s.
C├óu 9: Hai l├▓ xo c├│ ─æß╗Ö cß╗®ng l├Ā \({{K}_{1}}\), \({{K}_{2}}\) v├Ā mß╗Öt vß║Łt nß║Ęng \(m=1kg.\) Khi mß║»c hai l├▓ xo song song th├¼ tß║Īo ra mß╗Öt con lß║»c dao ─æß╗Öng ─æiß╗üu h├▓a vß╗øi \({{\omega }_{1}}=10\sqrt{5}{rad}/{s}\;\), khi mß║»c nß╗æi tiß║┐p hai l├▓ xo th├¼ con lß║»c dao ─æß╗Öng vß╗øi \({{\omega }_{2}}=2\sqrt{30}{rad}/{s}\;\). Gi├Ī trß╗ŗ cß╗¦a \({{K}_{1}},{{K}_{2}}\) l├Ā
A. 200; 300.
B. 250; 250.
C. 300; 250.
D. 250; 350.
C├óu 10: Hai l├▓ xo \({{l}_{1}}\) v├Ā \({{l}_{2}}\) c├│ c├╣ng ─æß╗Ö d├Āi. Khi treo vß║Łt m v├Āo l├▓ xo \({{l}_{1}}\) th├¼ chu kß╗│ dao ─æß╗Öng cß╗¦a vß║Łt l├Ā \({{T}_{1}}=0,6\text{s}\), khi treo vß║Łt v├Āo l├▓ xo \({{l}_{2}}\) th├¼ chu kß╗│ dao ─æß╗Öng cß╗¦a vß║Łt l├Ā 0,8s. Nß╗æi hai l├▓ xo vß╗øi nhau ß╗¤ cß║Ż hai ─æß║¦u ─æß╗ā ─æŲ░ß╗Żc mß╗Öt l├▓ xo c├╣ng ─æß╗Ö d├Āi rß╗ōi treo vß║Łt v├Āo hß╗ć hai l├▓ xo th├¼ chu kß╗│ dao ─æß╗Öng cß╗¦a vß║Łt l├Ā
A. 1,000 s.
B. 0,240 s.
C. 0,692 s.
D. 0,480 s.
---(Nß╗Öi dung ─æß║¦y ─æß╗¦, chi tiß║┐t tß╗½ c├óu 11 ─æß║┐n c├óu 20 cß╗¦a t├Āi liß╗ću c├Īc em vui l├▓ng xem Online hoß║Ęc ─É─āng nhß║Łp v├Āo HOC247 ─æß╗ü tß║Żi vß╗ü m├Īy)---
ĐÁP ÁN
|
1-D |
2-C |
3-A |
4-C |
5-B |
6-A |
7-C |
8-D |
9-A |
10-D |
|
11-A |
12-D |
13-D |
14-C |
15-C |
16-B |
17-B |
18-A |
19-A |
20-A |
Tr├¬n ─æ├óy l├Ā mß╗Öt phß║¦n tr├Łch ─æoß║Īn nß╗Öi dung PhŲ░ŲĪng ph├Īp giß║Żi b├Āi to├Īn vß╗ü cß║»t gh├®p l├▓ xo m├┤n Vß║Łt L├Į 12 n─ām 2021-2022. ─Éß╗ā xem th├¬m nhiß╗üu t├Āi liß╗ću tham khß║Żo hß╗»u ├Łch kh├Īc c├Īc em chß╗Źn chß╗®c n─āng xem online hoß║Ęc ─æ─āng nhß║Łp v├Āo trang hoc247.net ─æß╗ā tß║Żi t├Āi liß╗ću vß╗ü m├Īy t├Łnh.
Hy vß╗Źng t├Āi liß╗ću n├Āy sß║Į gi├║p c├Īc em hß╗Źc sinh ├┤n tß║Łp tß╗æt v├Ā ─æß║Īt th├Ānh t├Łch cao trong hß╗Źc tß║Łp.
T├Āi liß╗ću li├¬n quan
TŲ░ liß╗ću nß╗Ģi bß║Łt tuß║¦n
- Xem thêm













