ńźŠĽÉ cung cŠļ•p th√™m t√†i liŠĽáu gi√ļp c√°c em hŠĽćc sinh lŠĽõp 12 √īn tŠļ≠p chuŠļ©n bŠĽč tr∆įŠĽõc k√¨ thi sŠļĮp tŠĽõi HOC247 giŠĽõi thiŠĽáu ńĎŠļŅn c√°c em t√†i liŠĽáu Ph∆į∆°ng ph√°p giŠļ£i c√°c b√†i to√°n ńĎŠļ°i c∆į∆°ng vŠĽĀ dao ńĎŠĽông ńĎiŠĽĀu h√≤a v√† con lŠļĮc l√≤ xo m√īn VŠļ≠t L√Ĺ 12 nńÉm 2021-2022 ńĎ∆įŠĽ£c HOC247 bi√™n tŠļ≠p v√† tŠĽēng hŠĽ£p. Hi vŠĽćng t√†i liŠĽáu n√†y sŠļĹ c√≥ √≠ch cho c√°c em, ch√ļc c√°c em c√≥ kŠļŅt quŠļ£ hŠĽćc tŠļ≠p tŠĽĎt!
1. PH∆Į∆†NG PH√ĀP GIŠļĘI
Ch√ļng ta cŠļßn nhŠĽõ lŠļ°i c√°c kiŠļŅn thŠĽ©c ŠĽü phŠļßn l√Ĺ thuyŠļŅt ńĎ√£ hŠĽćc, c√°c ńĎiŠĽÉm cŠļßn l∆įu √Ĺ l√†:
- GiŠļ£ sŠĽ≠ con lŠļĮc l√≤ xo dao ńĎŠĽông ńĎiŠĽĀu h√≤a vŠĽõi ph∆į∆°ng tr√¨nh \(x=Ac\text{os}\left( \omega t+\varphi \right)\). TŠļßn sŠĽĎ g√≥c cŠĽßa con lŠļĮc l√≤ xo l√† \(\omega =\sqrt{\frac{k}{m}}({rad}/{s)}\;\).
- ńźŠĽĎi vŠĽõi tr∆įŠĽĚng hŠĽ£p con lŠļĮc l√≤ xo thŠļ≥ng ńĎŠĽ©ng ta lu√īn c√≥ \(mg=k\Delta {{l}_{0}}\)
Trong ńĎ√≥ \(\Delta {{l}_{o}}\) l√† ńĎŠĽô biŠļŅn dŠļ°ng cŠĽßa l√≤ xo khi vŠļ≠t ŠĽü vŠĽč tr√≠ c√Ęn bŠļĪng. TŠĽę ńĎ√≥ ngo√†i c√°ch t√≠nh tŠļßn sŠĽĎ g√≥c khi biŠļŅt khŠĽĎi l∆įŠĽ£ng m cŠĽßa vŠļ≠t v√† ńĎŠĽô cŠĽ©ng k cŠĽßa l√≤ xo th√¨ ta c√≤n c√≥ thŠĽÉ t√≠nh ńĎ∆įŠĽ£c tŠļßn sŠĽĎ g√≥c khi biŠļŅt ńĎŠĽô biŠļŅn dŠļ°ng cŠĽßa l√≤ xo khi vŠļ≠t ŠĽü vŠĽč tr√≠ c√Ęn bŠļĪng bŠĽüi c√īng thŠĽ©c:
\(\left\{ \begin{align} & \omega =\sqrt{\frac{k}{m}} \\ & mg=k\Delta {{l}_{0}} \\ \end{align} \right.\Rightarrow \omega =\sqrt{\frac{g}{\Delta {{l}_{0}}}}\Rightarrow T=2\pi \sqrt{\frac{\Delta {{l}_{0}}}{g}}\Rightarrow f=\frac{1}{2\pi }\sqrt{\frac{g}{\Delta {{l}_{0}}}}\)
- Chu k√¨ cŠĽßa con lŠļĮc l√≤ xo tŠĽČ lŠĽá vŠĽõi cńÉn bŠļ≠c hai cŠĽßa khŠĽĎi l∆įŠĽ£ng m tŠĽČ lŠĽá nghŠĽčch vŠĽõi cńÉn bŠļ≠c hai cŠĽßa k, chŠĽČ phŠĽ• thuŠĽôc v√†o m v√† k.
2. V√ć DŠĽ§ MINH HŠĽĆA
V√≠ dŠĽ• 1: MŠĽôt vŠļ≠t nhŠĽŹ khŠĽĎi l∆įŠĽ£ng 100g dao ńĎŠĽông theo ph∆į∆°ng tr√¨nh \(x=8\cos 10t\) ( x t√≠nh bŠļĪng cm, t t√≠nh bŠļĪng s). ńźŠĽông nńÉng cŠĽĪc ńĎŠļ°i cŠĽßa vŠļ≠t bŠļĪng:
A. 32mJ.
B. 64mJ.
C. 16mJ.
D. 128mJ.
H∆įŠĽõng dŠļęn giŠļ£i
ńźŠĽông nńÉng cŠĽĪc ńĎŠļ°i cŠĽßa vŠļ≠t ch√≠nh l√† c∆° nńÉng trong dao ńĎŠĽông, ta c√≥:
\(W=\frac{1}{2}m{{\omega }^{2}}{{A}^{2}}=\frac{0,{{1.10}^{2}}.0,{{08}^{2}}}{3}=32mJ.\)
ńź√°p √°n A.
V√≠ dŠĽ• 2: MŠĽôt vŠļ≠t dao ńĎŠĽông vŠĽõi ph∆į∆°ng tr√¨nh \(x=5\cos \left( 4\pi t+\frac{\pi }{6} \right).\) TŠļ°i thŠĽĚi ńĎiŠĽÉm t = 1s h√£y x√°c ńĎŠĽčnh li ńĎŠĽô cŠĽßa dao ńĎŠĽông
A. 2,5cm.
B. 5cm.
C. \(2,5\sqrt{3}\)cm.
D. \(2,5\sqrt{2}\)cm.
H∆įŠĽõng dŠļęn giŠļ£i
TŠļ°i thŠĽĚi ńĎiŠĽÉm t = 1s ta c√≥ \(x=5\cos \left( 4\pi .1+\frac{\pi }{6} \right)=2,5\sqrt{3}.\)
ńź√°p √°n C.
V√≠ dŠĽ• 3: Khi gŠļĮn quŠļ£ nŠļ∑ng m1 v√†o l√≤ xo, n√≥ dao ńĎŠĽông vŠĽõi chu k√¨ T1 = 1,2s. Khi gŠļĮn quŠļ£ nŠļ∑ng m2 v√†o l√≤ xo, n√≥ dao ńĎŠĽông vŠĽõi chu k√¨ T2 = 1,6s. Khi gŠļĮn ńĎŠĽďng thŠĽĚi m1 v√† m2 v√†o l√≤ xo ńĎ√≥, ch√ļng dao ńĎŠĽông vŠĽõi chu k√¨ bao nhi√™u?
A. 2 s.
B. 3 s.
C. 8 s.
D. 5 s.
H∆įŠĽõng dŠļęn giŠļ£i
ChŠĽČ cŠļßn nhŠļ≠n x√©t ńĎ∆°n giŠļ£n l√† chu k√¨ tŠĽČ lŠĽá thuŠļ≠n vŠĽõi \(\sqrt{m}\) n√™n khŠĽĎi l∆įŠĽ£ng m tŠĽČ lŠĽá thuŠļ≠n vŠĽõi \({{T}^{2}}\). TŠĽę ńĎ√Ęy khi gŠļĮn ńĎŠĽďng thŠĽĚi m1 v√† m2 v√†o th√¨ chu k√¨ l√ļc n√†y ńĎ∆įŠĽ£c x√°c ńĎŠĽčnh bŠĽüi \({{T}^{2}}={{T}_{1}}^{2}+{{T}_{2}}^{2}\)
NŠļŅu kh√īng quen vŠĽõi c√°ch giŠļ£i th√≠ch n√†y ta c√≥ thŠĽÉ l√†m nh∆į sau:
\(\left\{ \begin{align} & {{T}_{1}}=2\pi \sqrt{\frac{{{m}_{1}}}{k}} \\ & {{T}_{2}}=2\pi \sqrt{\frac{{{m}_{2}}}{k}} \\ & T=2\pi \sqrt{\frac{{{m}_{1}}+{{m}_{2}}}{k}} \\ \end{align} \right.\Rightarrow {{T}^{2}}={{(2\pi )}^{2}}\left( \frac{{{m}_{1}}}{k}+\frac{{{m}_{2}}}{k} \right)={{T}_{1}}^{2}+{{T}_{2}}^{2}\)
Thay sŠĽĎ ta ńĎ∆įŠĽ£c T = 2s.
ńź√°p √°n A.
V√≠ dŠĽ• 4: Vi√™n bi m1 gŠļĮn v√†o l√≤ xo c√≥ ńĎŠĽô cŠĽ©ng k th√¨ hŠĽá dao ńĎŠĽông vŠĽõi chu k√¨ T1 = 0,3s. Vi√™n bi m2 gŠļĮn v√†o l√≤ xo c√≥ ńĎŠĽô cŠĽ©ng k th√¨ hŠĽá dao ńĎŠĽông vŠĽõi chu k√¨ T2 = 0,4s. HŠĽŹi nŠļŅu vŠļ≠t c√≥ khŠĽĎi l∆įŠĽ£ng \(m=4{{m}_{1}}+3{{m}_{2}}\) v√†o l√≤ xo c√≥ ńĎŠĽô cŠĽ©ng k th√¨ hŠĽá c√≥ chu k√¨ dao ńĎŠĽông l√† bao nhi√™u?
A. 0,4 s.
B. 0,916 s.
C. 0,6 s.
D. 0,7 s.
H∆įŠĽõng dŠļęn giŠļ£i
V√¨ khŠĽĎi l∆įŠĽ£ng m tŠĽČ lŠĽá thuŠļ≠n vŠĽõi \({{T}^{2}}\) n√™n ta c√≥ khi treo vŠļ≠t c√≥ khŠĽĎi l∆įŠĽ£ng \(m=4{{m}_{1}}+3{{m}_{2}}\) v√†o l√≤ xo k th√¨ hŠĽá c√≥ chu k√¨ dao ńĎŠĽông ńĎ∆įŠĽ£c x√°c ńĎŠĽčnh bŠĽüi \({{T}^{2}}=4{{T}_{1}}^{2}+3{{T}_{2}}^{2}\). Thay sŠĽĎ v√†o ta t√≠nh ńĎ∆įŠĽ£c T = 0,916 s.
ńź√°p √°n B.
V√≠ dŠĽ• 5: MŠĽôt vŠļ≠t dao ńĎŠĽông ńĎiŠĽĀu h√≤a vŠĽõi gia tŠĽĎc cŠĽĪc ńĎŠļ°i l√† 200 cm/s2 v√† tŠĽĎc ńĎŠĽô cŠĽĪc ńĎŠļ°i l√† 20cm/s. HŠĽŹi khi vŠļ≠t c√≥ gia tŠĽĎc l√† 100 cm/s2 th√¨ tŠĽĎc ńĎŠĽô dao ńĎŠĽông cŠĽßa vŠļ≠t l√ļc ńĎ√≥ l√†
A. 10 cm/s.
B. \(10\sqrt{2}\)cm/s.
C. \(5\sqrt{3}\)cm/s.
D. \(10\sqrt{3}\)cm/s.
H∆įŠĽõng dŠļęn giŠļ£i
ńźŠĽĀ b√†i cho gia tŠĽĎc hŠĽŹi vŠļ≠n tŠĽĎc n√™n ta nhŠĽõ ngay ńĎŠļŅn c√īng thŠĽ©c ńĎŠĽôc lŠļ≠p thŠĽĚi gian giŠĽĮa a v√† v l√†: \({{\left( \frac{a}{{{a}_{\max }}} \right)}^{2}}+{{\left( \frac{v}{{{v}_{\max }}} \right)}^{2}}=1\). Thay sŠĽĎ v√†o ta t√≠nh ńĎ∆įŠĽ£c \(\left| v \right|\)= \)10\sqrt{3}\).
ńź√°p √°n D.
V√≠ dŠĽ• 6: C√≥ ba l√≤ xo giŠĽĎng nhau ńĎ∆įŠĽ£c ńĎŠļ∑t tr√™n mŠļ∑t phŠļ≥ng ngang, l√≤ xo thŠĽ© nhŠļ•t gŠļĮn vŠļ≠t nŠļ∑ng \({{m}_{1}}\)= 0,1kg; vŠļ≠t nŠļ∑ng \({{m}_{2}}\)= 300g ńĎ∆įŠĽ£c gŠļĮn v√†o l√≤ xo thŠĽ© 2; vŠļ≠t nŠļ∑ng \({{m}_{3}}\)= 0,4kg gŠļĮn v√†o l√≤ xo 3. CŠļ£ ba vŠļ≠t ńĎŠĽĀu c√≥ thŠĽÉ dao ńĎŠĽông kh√īng ma s√°t tr√™n mŠļ∑t phŠļ≥ng ngang. Ban ńĎŠļßu k√©o cŠļ£ 3 vŠļ≠t ra mŠĽôt ńĎoŠļ°n bŠļĪng nhau rŠĽďi bu√īng tay kh√īng vŠļ≠n tŠĽĎc ńĎŠļßu c√Ļng mŠĽôt l√ļc. HŠĽŹi vŠļ≠t nŠļ∑ng n√†o vŠĽĀ vŠĽč tr√≠ c√Ęn bŠļĪng ńĎŠļßu ti√™n?
A. vŠļ≠t 1.
B. vŠļ≠t 2.
C. vŠļ≠t 3.
D. 3 vŠļ≠t vŠĽĀ c√Ļng l√ļc.
H∆įŠĽõng dŠļęn giŠļ£i
V√¨ ban ńĎŠļßu k√©o cŠļ£ 3 vŠļ≠t ra mŠĽôt ńĎoŠļ°n bŠļĪng nhau n√™n muŠĽĎn biŠļŅt vŠļ≠t n√†o vŠĽĀ vŠĽč tr√≠ c√Ęn bŠļĪng ńĎŠļßu ti√™n th√¨ ta phŠļ£i so s√°nh chu k√¨ cŠĽßa 3 vŠļ≠t. VŠļ≠t n√†o c√≥ chu k√¨ c√†ng nhŠĽŹ th√¨ dao ńĎŠĽông c√†ng nhanh v√† ng∆įŠĽ£c lŠļ°i. Khi ńĎŠĽô cŠĽ©ng cŠĽßa l√≤ xo giŠĽĎng nhau th√¨ chu k√¨ tŠĽČ lŠĽá thuŠļ≠n vŠĽõi cńÉn bŠļ≠c hai cŠĽßa khŠĽĎi l∆įŠĽ£ng, m√† \({{m}_{1}}<{{m}_{2}}<{{m}_{3}}\) n√™n \({{T}_{1}}<{{T}_{2}}<{{T}_{3}}\), do ńĎ√≥ vŠļ≠t 1 sŠļĹ vŠĽĀ vŠĽč tr√≠ c√Ęn bŠļĪng tr∆įŠĽõc vŠļ≠t 2 v√† vŠļ≠t 3.
ńź√°p √°n A.
V√≠ dŠĽ• 7: Ba con lŠļĮc l√≤ xo c√≥ ńĎŠĽô cŠĽ©ng lŠļßn l∆įŠĽ£t l√† k;2k;3k. ńź∆įŠĽ£c ńĎŠļ∑t tr√™n mŠļ∑t phŠļ≥ng ngang v√† song song vŠĽõi nhau. Con lŠļĮc 1 gŠļĮn v√†o ńĎiŠĽÉm A; con lŠļĮc 2 gŠļĮn v√†o ńĎiŠĽÉm B; con lŠļĮc 3 gŠļĮn v√†o ńĎiŠĽÉm C. BiŠļŅt AB = BC, l√≤ xo 1 gŠļĮn vŠļ≠t \({{m}_{1}}=m\); l√≤ xo 2 gŠļĮn vŠļ≠t \({{m}_{2}}=2m\), l√≤ xo 3 gŠļĮn vŠļ≠t \({{m}_{3}}\). Ban ńĎŠļßu k√©o l√≤ xo 1 ńĎoŠļ°n l√† a; l√≤ xo 2 mŠĽôt ńĎoŠļ°n l√† 2a; l√≤ xo 3 mŠĽôt ńĎoŠļ°n l√† \({{A}_{3}}\), rŠĽďi bu√īng tay c√Ļng mŠĽôt l√ļc. HŠĽŹi ban ńĎŠļßu phŠļ£i k√©o vŠļ≠t 3 ra mŠĽôt ńĎoŠļ°n l√† bao nhi√™u v√† khŠĽĎi l∆įŠĽ£ng \({{m}_{3}}\) l√† bao nhi√™u ńĎŠĽÉ trong qu√° tr√¨nh dao ńĎŠĽông th√¨ 3 vŠļ≠t lu√īn thŠļ≥ng h√†ng?
A. 3m; 3a.
B. 3m; 6a.
C. 6m; 6a.
D. 9m; 9a.
H∆įŠĽõng dŠļęn giŠļ£i
Tr∆įŠĽõc hŠļŅt, ńĎŠĽÉ trong qu√° tr√¨nh dao ńĎŠĽông 3 vŠļ≠t lu√īn thŠļ≥ng h√†ng th√¨ tŠļßn sŠĽĎ g√≥c cŠĽßa 3 vŠļ≠t phŠļ£i bŠļĪng nhau. Ta c√≥ \({{\omega }_{1}}={{\omega }_{2}}={{\omega }_{3}}\Leftrightarrow \sqrt{\frac{k}{m}}=\sqrt{\frac{2k}{2m}}=\sqrt{\frac{3k}{3m}}\Rightarrow {{m}_{3}}=3m\)
TiŠļŅp theo, v√¨ AB = BC v√† trong qu√° tr√¨nh dao ńĎŠĽông 3 vŠļ≠t lu√īn thŠļ≥ng h√†ng n√™n ta c√≥ \({{O}_{2}}{{m}_{2}}\) ch√≠nh l√† ńĎ∆įŠĽĚng trung b√¨nh cŠĽßa h√¨nh thang \({{O}_{1}}{{O}_{3}}{{m}_{3}}{{m}_{1}}.\)
TŠĽę ńĎ√≥ ta c√≥: \(2a=\frac{a+{{A}_{3}}}{2}\Rightarrow {{A}_{3}}=3a.\)
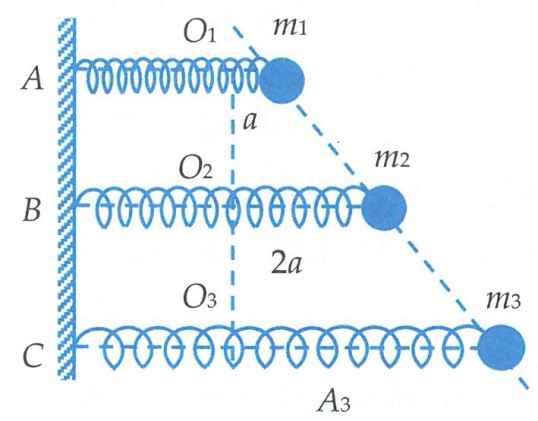
ńź√°p √°n A.
V√≠ dŠĽ• 8: MŠĽôt con lŠļĮc l√≤ xo gŠĽďm lo xo nhŠļĻ c√≥ ńĎŠĽô cŠĽ©ng 100 N/m v√† vŠļ≠t nhŠĽŹ c√≥ khŠĽĎi l∆įŠĽ£ng m. Con lŠļĮc dao ńĎŠĽông ńĎiŠĽĀu h√≤a theo ph∆į∆°ng ngang vŠĽõi chu k√¨ T. BiŠļŅt ŠĽü thŠĽĚi ńĎiŠĽÉm t vŠļ≠t c√≥ li ńĎŠĽô 5cm, ŠĽü thŠĽĚi ńĎiŠĽÉm \(t+\frac{T}{4}\)vŠļ≠t c√≥ vŠļ≠n tŠĽĎc 50 cm/s. Gi√° trŠĽč cŠĽßa m bŠļĪng:
A. 0,5kg.
B. 1,2kg.
C. 0,8kg.
D. 1,0kg.
H∆įŠĽõng dŠļęn giŠļ£i
V√¨ \({{t}_{2}}={{t}_{1}}+\frac{T}{4}\) n√™n nŠļŅu ta giŠļ£ sŠĽ≠ \({{x}_{1}}=A\cos \left( \omega {{t}_{1}} \right)\) th√¨
\({{x}_{2}}=A\cos \left( \omega \left( {{t}_{1}}+\frac{T}{4} \right) \right)=A\cos \left( \omega {{t}_{1}}+\frac{2\pi }{T}.\frac{T}{4} \right)=A\cos \left( \omega {{t}_{1}}+\frac{\pi }{2} \right)=-A\sin \left( \omega {{t}_{1}} \right)\)
TŠĽę ńĎ√≥ ta c√≥
\({{\sin }^{2}}\left( \omega {{t}_{1}} \right)+{{\cos }^{2}}\left( \omega {{t}_{1}} \right)=\frac{{{x}_{1}}^{2}}{{{A}^{2}}}+\frac{{{x}_{2}}^{2}}{{{A}^{2}}}=1\Leftrightarrow {{x}_{1}}^{2}+{{x}_{2}}^{2}={{A}^{2}}\Leftrightarrow {{x}_{1}}^{2}={{A}^{2}}-{{x}_{2}}^{2}\)
HoŠļ∑c ta c√≥ thŠĽÉ nhŠļ≠n x√©t nhanh l√† v√¨ \({{x}_{1}}\) v√† \({{x}_{2}}\) lŠĽách nhau vŠĽĀ g√≥c l√† \(\frac{\pi }{2}\) n√™n ta c√≥ lu√īn \(\frac{{{x}_{1}}^{2}}{{{A}^{2}}}+\frac{{{x}_{2}}^{2}}{{{A}^{2}}}=1\)
VŠļ≠y l√† ta ńĎ√£ t√≠nh xong \({{A}^{2}}-{{x}_{2}}^{2}\), thay v√†o biŠĽÉu thŠĽ©c ńĎŠĽôc lŠļ≠p thŠĽĚi gian ta c√≥ ngay:
\({{\left( \frac{{{v}_{2}}}{\omega } \right)}^{2}}={{A}^{2}}-{{x}_{2}}^{2}={{x}_{1}}^{2}\Rightarrow {{v}_{2}}=\omega {{x}_{1}}\Rightarrow {{v}_{2}}=\sqrt{\frac{k}{m}{{x}_{1}}}.\)
Thay sŠĽĎ ta c√≥ m = 1 kg.
ńź√°p √°n D.
3. B√ÄI TŠļ¨P TŠĽį LUYŠĽÜN
C√Ęu 1: GŠĽći k l√† ńĎŠĽô cŠĽ©ng cŠĽßa l√≤ xo, m l√† khŠĽĎi l∆įŠĽ£ng cŠĽßa vŠļ≠t nŠļ∑ng. BŠĽŹ qua ma s√°t khŠĽĎi l∆įŠĽ£ng cŠĽßa l√≤ xo v√† k√≠ch th∆įŠĽõc vŠļ≠t nŠļ∑ng. C√īng thŠĽ©c chu kŠĽ≥ cŠĽßa dao ńĎŠĽông?
A. \(T=2\pi \sqrt{\frac{k}{m}}.\)
B. \(T=2\pi \sqrt{\frac{m}{k}}.\)
C. \(T=2\pi \sqrt{km}.\)
D. \(T=2\pi \frac{m}{k}.\)
C√Ęu 2: H√£y t√¨m nhŠļ≠n x√©t ńĎ√ļng vŠĽĀ con lŠļĮc l√≤ xo.
A. Con lŠļĮc l√≤ xo c√≥ chu kŠĽ≥ tńÉng l√™n khi bi√™n ńĎŠĽô dao ńĎŠĽông tńÉng l√™n.
B. Con lŠļĮc l√≤ xo c√≥ chu kŠĽ≥ kh√īng phŠĽ• thuŠĽôc v√†o gia tŠĽĎc trŠĽćng tr∆įŠĽĚng.
C. Con lŠļĮc l√≤ xo c√≥ chu kŠĽ≥ giŠļ£m xuŠĽĎng khi khŠĽĎi l∆įŠĽ£ng vŠļ≠t nŠļ∑ng tńÉng l√™n.
D. Con lŠļĮc l√≤ xo c√≥ chu kŠĽ≥ phŠĽ• thuŠĽôc v√†o viŠĽác k√©o vŠļ≠t nhŠļĻ hay mŠļ°nh tr∆įŠĽõc khi bu√īng tay cho vŠļ≠t dao ńĎŠĽông.
C√Ęu 3: GŠĽći k l√† ńĎŠĽô cŠĽ©ng cŠĽßa l√≤ xo, m l√† khŠĽĎi l∆įŠĽ£ng cŠĽßa vŠļ≠t nńÉng. BŠĽŹ qua ma s√°t khŠĽĎi l∆įŠĽ£ng cŠĽßa l√≤ xo v√† k√≠ch th∆įŠĽõc vŠļ≠t nŠļ∑ng. NŠļŅu ńĎŠĽô cŠĽ©ng cŠĽßa l√≤ xo tńÉng gŠļ•p ńĎ√īi, khŠĽĎi l∆įŠĽ£ng vŠļ≠t dao ńĎŠĽông kh√īng thay ńĎŠĽēi th√¨ chu kŠĽ≥ dao ńĎŠĽông thay ńĎŠĽēi nh∆į thŠļŅ n√†o?
A. TńÉng 2 lŠļßn.
B. TńÉng \(\sqrt{2}\) lŠļßn.
C. GiŠļ£m 2 lŠļßn.
D. GiŠļ£m \(\sqrt{2}\) lŠļßn.
C√Ęu 4: MŠĽôt con lŠļĮc l√≤ xo treo thŠļ≥ng ńĎŠĽ©ng dao ńĎŠĽông vŠĽõi bi√™n ńĎŠĽô 10 cm, chu kŠĽ≥ 1s. KhŠĽĎi l∆įŠĽ£ng cŠĽßa quŠļ£ nŠļ∑ng 400g, lŠļ•y \({{\pi }^{2}}=10\), cho \(g=10\,\,{m}/{{{s}^{2}}.}\;\) ńźŠĽô cŠĽ©ng cŠĽßa l√≤ xo l√† bao nhi√™u?
A. \(16{N}/{m}\;.\)
B. \(20{N}/{m}\;.\)
C. \(32{N}/{m}\;.\)
D. \(40{N}/{m}\;.\)
C√Ęu 5: MŠĽôt con lŠļĮc l√≤ xo dao ńĎŠĽông vŠĽõi chu kŠĽ≥ \(T=0,4\,\,s\). NŠļŅu tńÉng bi√™n ńĎŠĽô dao ńĎŠĽông cŠĽßa con lŠļĮc l√™n 4 lŠļßn th√¨ chu kŠĽ≥ dao ńĎŠĽông cŠĽßa vŠļ≠t c√≥ thay ńĎŠĽēi nh∆į thŠļŅ n√†o?
A. TńÉng l√™n 2 lŠļßn.
B. GiŠļ£m 2 lŠļßn.
C. Kh√īng ńĎŠĽēi.
D. ńź√°p √°n kh√°c.
C√Ęu 6: Con lŠļĮc l√≤ xo dao ńĎŠĽông ńĎiŠĽĀu h√≤a vŠĽõi chu k√¨ \(T=0,4\,\,s\). ńźŠĽô cŠĽ©ng cŠĽßa l√≤ xo l√† \(100{N}/{m}\;\), t√¨m khŠĽĎi l∆įŠĽ£ng cŠĽßa vŠļ≠t?
A. 0,2 kg.
B. 0,4 kg.
C. 0,4 g.
D. ńź√°p √°n kh√°c.
C√Ęu 7: MŠĽôt con lŠļĮc l√≤ xo dao ńĎŠĽông vŠĽõi chu kŠĽ≥ \(T=0,4\,\,s\). NŠļŅu tńÉng khŠĽĎi l∆įŠĽ£ng cŠĽßa vŠļ≠t l√™n 4 lŠļßn th√¨ T thay ńĎŠĽēi nh∆į thŠļŅ n√†o?
A. TńÉng l√™n 2 lŠļßn.
B. GiŠļ£m 2 lŠļßn.
C. Kh√īng ńĎŠĽēi.
D. ńź√°p √°n kh√°c.
C√Ęu 8: MŠĽôt con lŠļĮc l√≤ xo gŠĽďm vi√™n bi nhŠĽŹ c√≥ khŠĽĎi l∆įŠĽ£ng m v√† l√≤ xo khŠĽĎi l∆įŠĽ£ng kh√īng ńĎ√°ng kŠĽÉ c√≥ ńĎŠĽô cŠĽ©ng k, dao ńĎŠĽông ńĎiŠĽĀu h√≤a theo ph∆į∆°ng thŠļ≥ng ńĎŠĽ©ng tŠļ°i n∆°i c√≥ gia tŠĽĎc r∆°i tŠĽĪ do l√† g. Khi vi√™n bi ŠĽü vŠĽč tr√≠ c√Ęn bŠļĪng, l√≤ xo d√£n mŠĽôt ńĎoŠļ°n \(\Delta l.\) C√īng thŠĽ©c t√≠nh chu kŠĽ≥ dao ńĎŠĽông ńĎiŠĽĀu h√≤a cŠĽßa con lŠļĮc l√†:
A. \(T=2\pi \sqrt{\frac{\Delta l}{g}}.\)
B. \(T=2\pi \sqrt{\frac{l}{g}}.\)
C. \(T=2\pi \sqrt{\frac{g}{l}}.\)
D. \(T=2\pi \sqrt{\frac{g}{\Delta l}}.\)
C√Ęu 9: MŠĽôt con lŠļĮc l√≤ xo gŠĽďm vŠļ≠t c√≥ khŠĽĎi l∆įŠĽ£ng m v√† l√≤ xo c√≥ ńĎŠĽô cŠĽ©ng k, dao ńĎŠĽông ńĎiŠĽĀu h√≤a. NŠļŅu tńÉng ńĎŠĽô cŠĽ©ng k l√™n 2 lŠļßn v√† giŠļ£m khŠĽĎi l∆įŠĽ£ng m ńĎi 8 lŠļßn th√¨ tŠļßn sŠĽĎ dao ńĎŠĽông cŠĽßa vŠļ≠t sŠļĹ?
A. TńÉng 2 lŠļßn.
B. TńÉng 4 lŠļßn.
C. TńÉng 2 lŠļßn.
D. GiŠļ£m 2 lŠļßn.
C√Ęu 10: MŠĽôt con lŠļĮc l√≤ xo gŠĽďm mŠĽôt vŠļ≠t c√≥ khŠĽĎi l∆įŠĽ£ng m v√† l√≤ xo c√≥ ńĎŠĽô cŠĽ©ng k kh√īng ńĎŠĽēi, dao ńĎŠĽông ńĎiŠĽĀu h√≤a. NŠļŅu khŠĽĎi l∆įŠĽ£ng m=400g th√¨ chu kŠĽ≥ dao ńĎŠĽông cŠĽßa con lŠļĮc l√† 2s. ńźŠĽÉ chu kŠĽ≥ cŠĽßa con lŠļĮc l√† 1s th√¨ khŠĽĎi l∆įŠĽ£ng m bŠļĪng
A. 200g. B. 0,1kg. C. 0,3kg. D. 400g.
C√Ęu 11: MŠĽôt vŠļ≠t treo v√†o l√≤ xo c√≥ khŠĽĎi l∆įŠĽ£ng kh√īng ńĎ√°ng kŠĽÉ, chiŠĽĀu d√†i tŠĽĪ nhi√™n \({{l}_{0}}\) ńĎŠĽô cŠĽ©ng k, treo thŠļ≥ng ńĎŠĽ©ng v√†o vŠļ≠t \({{m}_{1}}=100g\) v√†o l√≤ xo th√¨ chiŠĽĀu d√†i cŠĽßa n√≥ l√† 31 cm. Treo th√™m vŠļ≠t \({{m}_{2}}=100\,\,g\) v√†o l√≤ xo th√¨ chei√®u d√†i cŠĽßa l√≤ xo l√† 32 cm. Cho \(g=10{m}/{{{s}^{2}}}\;\), ńĎŠĽô cŠĽ©ng cŠĽßa l√≤ xo l√†:
A. \(10\,\,{N}/{m}\;.\)
B. \(0,10\,\,{N}/{m}\;.\)
C. \(1000\,\,{N}/{m}\;.\)
D. \(100\,\,{N}/{m}\;.\)
C√Ęu 12: MŠĽôt con lŠļĮc l√≤ xo dao ńĎŠĽông ńĎiŠĽĀu h√≤a theo ph∆į∆°ng thŠļ≥ng ńĎŠĽ©ng, tŠļ°i n∆°i c√≥ gia tŠĽĎc r∆°i tŠĽĪ do bŠļĪng g. ŠĽě vŠĽč tr√≠ c√Ęn bŠļĪng l√≤ xo d√£n ra mŠĽôt ńĎoŠļ°n \(\Delta l\). TŠļßn sŠĽĎ dao ńĎŠĽông cŠĽßa con lŠļĮc ńĎ∆įŠĽ£c x√°c ńĎŠĽčnh theo c√īng thŠĽ©c:
A. \(2\pi \sqrt{\frac{\Delta l}{g}}.\)
B. \(\frac{1}{2\pi }\sqrt{\frac{\Delta l}{g}}.\)
C. \(\frac{1}{2\pi }\sqrt{\frac{g}{\Delta l}}.\)
D. \(2\pi \sqrt{\frac{g}{\Delta l}}.\)
C√Ęu 13: MŠĽôt vŠļ≠t treo v√†o l√≤ xo l√†m n√≥ d√£n ra 4cm. LŠļ•y \({{\pi }^{2}}=10\), cho \(g=10{m}/{{{s}^{2}}}\;\). TŠļßn sŠĽĎ dao ńĎŠĽông cŠĽßa vŠļ≠t l√†
A. 2,5 Hz/ B. 5,0 Hz. C. 4,5 Hz. D. 2,0 Hz.
C√Ęu 14: GŠĽći k l√† ńĎŠĽô cŠĽ©ng cŠĽßa l√≤ xo, m l√† khŠĽĎi l∆įŠĽ£ng cŠĽßa vŠļ≠t nŠļ∑ng. BŠĽŹ qua ma s√°t khŠĽĎi l∆įŠĽ£ng cŠĽßa l√≤ xo v√† k√≠ch th∆įŠĽõc vŠļ≠t nŠļ∑ng. NŠļŅu ńĎŠĽô cŠĽ©ng cŠĽßa l√≤ xo tńÉng gŠļ•p ńĎ√īi, khŠĽĎi l∆įŠĽ£ng vŠļ≠t dao ńĎŠĽông tńÉng gŠļ•p ba th√¨ chu kŠĽ≥ dao ńĎŠĽông tńÉng gŠļ•p:
A. 6 lŠļßn.
B. \(\sqrt{\frac{3}{2}}\) lŠļßn.
C. \(\sqrt{\frac{2}{3}}\) lŠļßn.
D. \(\frac{3}{2}\) lŠļßn
C√Ęu 15: Khi gŠļĮn quŠļ£ nŠļ∑ng \({{m}_{1}}\) v√†o l√≤ xo, n√≥ dao ńĎŠĽông ńĎiŠĽĀu h√≤a vŠĽõi chu kŠĽ≥ \({{T}_{1}}=1,2\text{s}\). Khi gŠļĮn quŠļ£ nŠļ∑ng \({{m}_{2}}\) v√†o l√≤ xo tr√™n n√≥ dao ńĎŠĽông vŠĽõi chu kŠĽ≥ \(1,6\text{s}\). Khi gŠļĮn ńĎŠĽďng thŠĽĚi hai vŠļ≠t \({{m}_{1}}\) v√† \({{m}_{2}}\) th√¨ chu kŠĽ≥ dao ńĎŠĽông cŠĽßa ch√ļng l√†
A. 1,4 s. B. 2,0 s. C. 2,8 s. D. 4,0 s.
---(NŠĽôi dung ńĎŠļßy ńĎŠĽß, chi tiŠļŅt tŠĽę c√Ęu 16 ńĎŠļŅn c√Ęu 50 cŠĽßa t√†i liŠĽáu c√°c em vui l√≤ng xem Online hoŠļ∑c ńźńÉng nhŠļ≠p v√†o HOC247 ńĎŠĽĀ tŠļ£i vŠĽĀ m√°y)---
ńź√ĀP √ĀN
|
1-B |
2-B |
3-D |
4-A |
5-C |
6-B |
7-A |
8-A |
9-B |
10-B |
|
11-D |
12-C |
13-A |
14-B |
15-B |
16-D |
17-C |
18-C |
19-C |
20-A |
|
21-D |
22-C |
23-C |
24-C |
25-C |
26-B |
27-D |
28-C |
29-C |
30-D |
|
31-B |
32-A |
33-D |
34-B |
35-B |
36-A |
37-C |
38-B |
39-B |
40-B |
|
41-B |
42-A |
43-A |
44-C |
45-C |
46-B |
47-A |
48-D |
49-B |
50-A |
Tr√™n ńĎ√Ęy l√† mŠĽôt phŠļßn tr√≠ch ńĎoŠļ°n nŠĽôi dung Ph∆į∆°ng ph√°p giŠļ£i c√°c b√†i to√°n ńĎŠļ°i c∆į∆°ng vŠĽĀ dao ńĎŠĽông ńĎiŠĽĀu h√≤a v√† con lŠļĮc l√≤ xo m√īn VŠļ≠t L√Ĺ 12 nńÉm 2021-2022. ńźŠĽÉ xem th√™m nhiŠĽĀu t√†i liŠĽáu tham khŠļ£o hŠĽĮu √≠ch kh√°c c√°c em chŠĽćn chŠĽ©c nńÉng xem online hoŠļ∑c ńĎńÉng nhŠļ≠p v√†o trang hoc247.net ńĎŠĽÉ tŠļ£i t√†i liŠĽáu vŠĽĀ m√°y t√≠nh.
Hy vŠĽćng t√†i liŠĽáu n√†y sŠļĹ gi√ļp c√°c em hŠĽćc sinh √īn tŠļ≠p tŠĽĎt v√† ńĎŠļ°t th√†nh t√≠ch cao trong hŠĽćc tŠļ≠p.
T√†i liŠĽáu li√™n quan
T∆į liŠĽáu nŠĽēi bŠļ≠t tuŠļßn
- Xem thêm