Phần hướng dẫn giải bài tập SGK Toán 9 Bài 1 Phương trình bậc nhất hai ẩn sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các dạng bài tập từ SGK Toán 9.
-
Bài tập 1 trang 7 SGK Toán 9 Tập 2
Trong các cặp số \((-2; 1),(0;2); (-1; 0), (1,5; 3)\) và \((4; -3)\), cặp số nào là nghiệm của phương trình:
a) \(5x + 4y = 8\) b) \(3x + 5y = -3\)
-
Bài tập 2 trang 7 SGK Toán 9 Tập 2
Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ đường thẳng biểu diễn tập nghiệm của nó:
a) \(3x - y = 2\) b) \(x + 5y = 3\)
c) \(4x - 3y = -1\) d) \(x +5y = 0\)
e) \(4x + 0y = -2\) f) \(0x + 2y = 5\)
-
Bài tập 3 trang 7 SGK Toán 9 Tập 2
Cho hai phương trình \(x + 2y = 4\) và \(x - y = 1\). Vẽ hai đường thẳng biểu diễn tập nghiệm của hai phương trình đó trên cùng một hệ trục tọa độ. Xác định tọa độ giao điểm của hai đường thẳng và cho biết tọa độ của nó là nghiệm của các phương trình nào.
-
Bài tập 1 trang 5 SBT Toán 9 Tập 2
Cho các cặp số và các phương trình sau. Hãy dùng mũi tên (như trong hình vẽ) chỉ rõ mỗi cặp số là nghiệm của những phương trình nào:
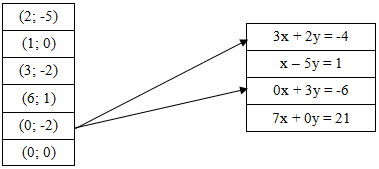
-
Bài tập 2 trang 5 SBT Toán 9 Tập 2
Viết nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm của mỗi phương trình sau:
\(a)\) \(2x - y = 3\)
\(b)\) \(x + 2y = 4\)
\(c)\) \(3x - 2y = 6\)
\(d)\) \(2x + 3y = 5\)
\(e)\) \(0x + 5y = - 10\)
\(f)\) \( - 4x + 0y = - 12\)
-
Bài tập 3 trang 5 SBT Toán 9 Tập 2
Trong mỗi trường hợp sau hãy tìm giá trị của m để:
a) Điểm M(1 ; 0) thuộc đường thẳng mx - 5y = 7
b) Điểm N(0 ; -3) thuộc đường thẳng 2,5x + my = -21
c) Điểm P(5; -3) thuộc đường thẳng mx + 2y = -1
d) Điểm P(5; -3) thuộc đường thẳng 3x – my = 6.
e) Điểm Q(0,5; -3) thuộc đường thẳng mx + 0y = 17,5
f) Điểm S(4; 0,3) thuộc đường thẳng 0x + my = 1,5
g) Điểm A(2; -3) thuộc đường thẳng (m – 1)x + (m + 1)y = 2m + 1
-
Bài tập 4 trang 6 SBT Toán 9 Tập 2
Phương trình nào sau đây xác định 1 hàm số dạng y = ax + b?
a) 5x – y = 7 c) 3x + 5y = 10
b) 0x + 3y = -1 d) 6x – 0y = 18
-
Bài tập 5 trang 6 SBT Toán 9 Tập 2
Phải chọn \(a\) và \(b\) như thế nào để phương trình \(ax + by = c\) xác định một hàm số bậc nhất của biến \(x\)?
-
Bài tập 6 trang 6 SBT Toán 9 Tập 2
Vẽ mỗi cặp đường thẳng sau trong cùng 1 mặt phẳng tọa độ rồi tìm tọa độ giao điểm của 2 đường thẳng đó
a) 2x + y = 1 và 4x – 2y = -10
b) 0,5x + 0,25y = 0,15 và \( - {1 \over 2}x + {1 \over 6}y = - {3 \over 2}\)
c) 4x + 5y = 20 và 0,8x + y = 4
d) 4x + 5y = 20 và 2x + 2,5y = 5
-
Bài tập 7 trang 6 SBT Toán 9 Tập 2
Giải thích vì sao khi \(M\left( {{x_0};{y_0}} \right)\) là giao điểm của hai đường thẳng \(ax + by = c\) và \(a'x + b'y = c'\) thì \(\left( {{x_0};{y_0}} \right)\) là nghiệm chung của hai phương trình ấy.
-
Bài tập 1.1 trang 6 SBT Toán 9 Tập 2
Điểm nào sau đây thuộc đường thẳng \(3x – 2y = 3:\)
\(A(1 ; 3);\) \( B(2 ; 3);\)
\(C(3 ; 3);\) \(D(4 ; 3)?\)
-
Bài tập 1.2 trang 6 SBT Toán 9 Tập 2
Trong mỗi trường hợp sau, hãy xác định đường thẳng \(ax + by = c\) đi qua hai điểm \(M\) và \(N\) cho trước
\(a) M (0 ; -1), N (3 ; 0)\)
\(b) M (0 ; 3), N (-1 ; 0)\)






