Giải bài 16 tr 52 sách BT Toán lớp 9 Tập 2
Giải các phương trình:
a) \(5{x^2} - 20 = 0\)
b) \( - 3{x^2} + 15 = 0\)
c) \(1,2{x^2} - 0,192 = 0\)
d) \(1172,5{x^2} + 42,18 = 0\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) \({x^2} = a > 0 \Leftrightarrow x = \pm \sqrt a \)
+) \(x^2\ge 0\) với \(\forall x.\)
Lời giải chi tiết
a) \(5{x^2} - 20x = 0 \Leftrightarrow {x^2} = 4 \Leftrightarrow \left| x \right| = 2\)
⇔ x = 2 hoặc x = -2
Vậy phương trình có hai nghiệm: \({x_1} = 2;{x_2} = - 2\)
b) \( - 3{x^2} + 15 = 0 \Leftrightarrow {x^2} = 5 \Leftrightarrow \left| x \right| = \sqrt 5 \)
⇔ \(x = \sqrt 5 \) hoặc \(x = - \sqrt 5 \)
Vậy phương trình có hai nghiệm: \({x_1} = \sqrt 5 ;{x_2} = - \sqrt 5 \)
c) \(1,2{x^2} - 0,192 = 0 \Leftrightarrow {x^2} = 0,16 \Leftrightarrow \left| x \right| = 0,4\)
\( \Leftrightarrow x = 0,4\) hoặc x = -0,4
Vậy phương trình có hai nghiệm: \({x_1} = 0,4;{x_2} = - 0,4\)
d) \(1172,5{x^2} + 42,18 = 0\)
Ta có: \({x^2} \ge 0;1172,5{x^2} \ge 0;1172,5{x^2} + 42,18 > 0\) nên không có giá trị nào của x để \(1172,5{x^2} + 42,18 = 0\)
Phương trình đã cho vô nghiệm.
-- Mod Toán 9 HỌC247
-


Giải phương trình \(2{x^2} - 8x = - 1\).
bởi thanh hằng
 17/02/2021
Theo dõi (0) 1 Trả lời
17/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình \({x^2} - 4x = - \dfrac{1}{2}\).
bởi Minh Hanh
 18/02/2021
Theo dõi (0) 1 Trả lời
18/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình \({x^2} - 4x + 4 = \dfrac{7}{2}\)
bởi Hoàng giang
 17/02/2021
Theo dõi (0) 1 Trả lời
17/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình \({\left( {x - 2} \right)^2} = \dfrac{7}{2}\) bằng cách điền vào các chỗ trống \(\left( {...} \right)\) trong các đẳng thức: \({\left( {x - 2} \right)^2} = \dfrac{7}{2} \Leftrightarrow x - 2 = ... \Leftrightarrow x = ...\). Vậy phương trình có hai nghiệm là: \({x_1} = ...;{x_2} = ...\)
bởi Lê Nhật Minh
 17/02/2021
Theo dõi (0) 1 Trả lời
17/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình \(3{x^2} - 2 = 0\)
bởi May May
 18/02/2021
Theo dõi (0) 1 Trả lời
18/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình \(2x^2 + 5x = 0\) bằng cách đặt nhân tử chung để đưa nó về phương trình tích.
bởi bach hao
 18/02/2021
Theo dõi (0) 1 Trả lời
18/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình \( - 10{x^2} + 40 = 0\)
bởi Tram Anh
 21/01/2021
21/01/2021
A. Vô nghiệm
B. x = 2
C. x = 4
D . x = ±2
Theo dõi (0) 1 Trả lời -


Cho phương trình \(2{x^3} + 2{x^2} - 3x + 10 = 2{x^3} + {x^2}--10\). Sau khi biến đổi đưa phương trình trên về dạng ax2 + bx+ c =0 thì hệ số a bằng ?
bởi Thùy Nguyễn
 21/01/2021
21/01/2021
A. 2
B.1
C. 3
D. -1
Theo dõi (0) 1 Trả lời -


Cho phương trình \(2{x^2}--10x + 100 = - 2x + 10\). Sau khi đưa phương trình trên về dạng \(a{x^2} + bx + c = 0\) thì hệ số b là?
bởi Van Tho
 20/01/2021
20/01/2021
A. -8
B . -12
C. 12
D. 8
Theo dõi (0) 1 Trả lời -


A. x2 + 4x - 7 = x2 + 8x - 10
B. x3 + 8x = 0
C. x2 - 4 = 0
D. 5x - 1 = 0
Theo dõi (0) 1 Trả lời -


Hệ số c của phương trình \({x^2} + 7x + 9 = 9\) là?
bởi Bao Nhi
 20/01/2021
20/01/2021
A. 9
B. -9
C. 0
D. 18
Theo dõi (0) 1 Trả lời -


Giải phương trình \(2x^4-5x^2+3=0\)?
bởi Tây Nguyễn
 29/06/2020
29/06/2020
Giúp mình với
Theo dõi (0) 4 Trả lời -


Chứng tỏ phương trình có 2 nghiệm với mọi m?
bởi Huyền Trân
 09/06/2020
09/06/2020
Câu 3
 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Cho pt \(x^2+mx-3=0\) . Tìm m để \( 2{x_1}+{x_2}=1\)?
bởi Mary Tran
 02/06/2020
02/06/2020
Cho pt x^2+mx-3=0. Tìm m để 2x1+x2=1
Theo dõi (0) 0 Trả lời -


Giải BPT khi m=2?
bởi Trần Quang
 30/05/2020
30/05/2020
Giúp mình với ạ
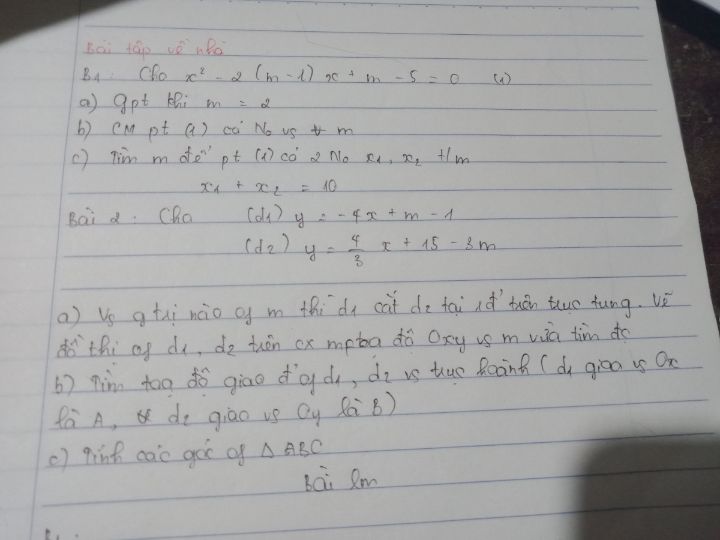 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Rút gọn A?
bởi Ngọc Bích
 26/05/2020
26/05/2020
Mọi người giúp em 3 bài này vs ạ
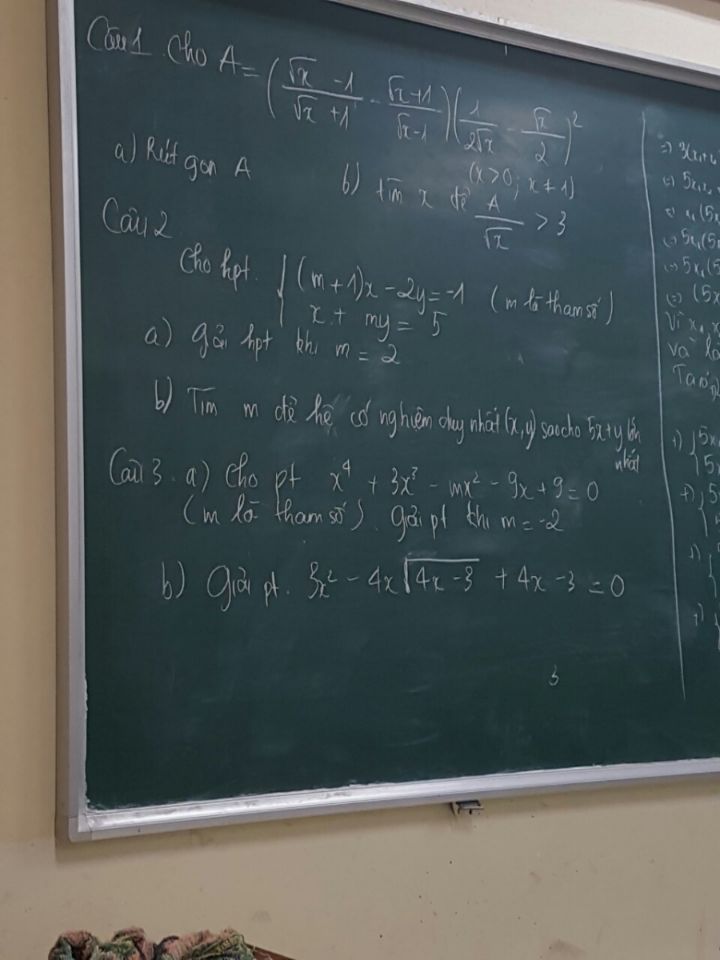 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Giải và biện luận phương trình 2x^2-3x-m-1=0
bởi Hân Nguyễn
 22/04/2020
Giai giup minh nhe
22/04/2020
Giai giup minh nhe Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Đồ thị hàm số y=x^2 đi qua điểm nào
bởi Hoàng khánh Hân
 20/04/2020
20/04/2020
Câu 1: Đths y=-3x2 đi qua điểm C(c;-6).Khi đó c bằng :
A.√2
B.-√2
C.+- √2
D.kết quả khác
Câu 2 Đths y=ax2 cắt đường thẳng y=-2x+3 tại điểm có hoành độ bằng:
A.1
B.-1
C.√5
D.+-√5
Câu 3: Điểm N(2;-5) thuộc đths y=mx2+3 khi m bằng:
A.-2
B.2
C.1/2
D.-1/2
Câu 4: Đths y=x2 đi qua điểm :
A(0;1)
B.(-1;1)
C.(1;-1)
D.(1;0)
Câu 5 Hàm số y=(m-1/2)x2 đồng biến khi x>0 nếu:
A.m<1/2
B.m>1/2
C.m>-1/2
D.m=1/2
Theo dõi (0) 0 Trả lời





