Giải bài 17 tr 52 sách BT Toán lớp 9 Tập 2
Giải các phương trình:
a) \({\left( {x - 3} \right)^2} = 4\)
b) \({\left( {{1 \over 2} - x} \right)^2} - 3 = 0\)
c) \({\left( {2x - \sqrt 2 } \right)^2} - 8 = 0\)
d) \({\left( {2,1x - 1,2} \right)^2} - 0,25 = 0\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Đưa phương trình đã cho về phương trình tích.
Lời giải chi tiết
a)
\(\eqalign{
& {\left( {x - 3} \right)^2} = 4 \Leftrightarrow {\left( {x - 3} \right)^2} - {2^2} = 0 \cr
& \Leftrightarrow \left[ {\left( {x - 3} \right) + 2} \right]\left[ {\left( {x - 3} \right) - 2} \right] = 0 \cr
& \Leftrightarrow \left( {x - 1} \right)\left( {x - 5} \right) = 0 \cr} \)
⇔ x – 1 = 0 hoặc x – 5 = 0
⇔ x = 1 hoặc x = 5
Vậy phương trình có hai nghiệm: \({x_1} = 1;{x_2} = 5\)
b)
\(\eqalign{
& {\left( {{1 \over 2} - x} \right)^2} - 3 = 0 \Leftrightarrow \left[ {\left( {{1 \over 2} - x} \right) + \sqrt 3 } \right]\left[ {\left( {{1 \over 2} - x} \right) - \sqrt 3 } \right] = 0 \cr
& \Leftrightarrow \left( {{1 \over 2} + \sqrt 3 - x} \right)\left( {{1 \over 2} - \sqrt 3 - x} \right) = 0 \cr} \)
⇔ \({1 \over 2} + \sqrt 3 - x = 0\) hoặc \({1 \over 2} - \sqrt 3 - x = 0\)
\( \Leftrightarrow x = {1 \over 2} + \sqrt 3 \) hoặc \(x = {1 \over 2} - \sqrt 3 \)
Vậy phương trình có hai nghiệm: \({x_1} = {1 \over 2} = \sqrt 3 ;{x_2} = {1 \over 2} - \sqrt 3 \)
c) \({\left( {2x - \sqrt 2 } \right)^2} - 8 = 0 \Leftrightarrow {\left( {2x - \sqrt 2 } \right)^2} - {\left( {2\sqrt 2 } \right)^2} = 0\)
\(\eqalign{
& \Leftrightarrow \left[ {\left( {2x - \sqrt 2 } \right) + 2\sqrt 2 } \right]\left[ {\left( {2x - \sqrt 2 } \right) - 2\sqrt 2 } \right] = 0 \cr
& \Leftrightarrow \left( {2x + \sqrt 2 } \right)\left( {2x - 3\sqrt 2 } \right) = 0 \cr} \)
⇔ \(2x + \sqrt 2 = 0\) hoặc \(2x - 3\sqrt 2 = 0\)
\( \Leftrightarrow x = - {{\sqrt 2 } \over 2}\) hoặc \(x = {{3\sqrt 2 } \over 2}\)
Vậy phương trình có hai nghiệm: \({x_1} = - {{\sqrt 2 } \over 2};{x_2} = {{3\sqrt 2 } \over 2}\)
d) \({\left( {2,1x - 1,2} \right)^2} - 0,25 = 0 \Leftrightarrow {\left( {2,1x - 1,2} \right)^2} - {\left( {0,5} \right)^2} = 0\)
\(\eqalign{
& \Leftrightarrow \left( {2,1x - 1,2 + 0,5} \right)\left( {2,1x - 1,2 - 0,5} \right) = 0 \cr
& \Leftrightarrow \left( {2,1x - 0,7} \right)\left( {2,1x - 1,7} \right) = 0 \cr} \)
\( \Leftrightarrow 2,1x - 0,7 = 0\) hoặc \(2,1x - 1,7 = 0\)
\( \Leftrightarrow x = {1 \over 3}\) hoặc \(x = {{17} \over {21}}\)
Vậy phương trình có hai nghiệm: \({x_1} = {1 \over 3};{x_2} = {{17} \over {21}}\)
-- Mod Toán 9 HỌC247
-


Giải phương trình x^2+x+6=0
bởi Ánh Phụng
 20/04/2020
20/04/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình x^2-2x=0
bởi Ze Hùng
 17/04/2020
17/04/2020
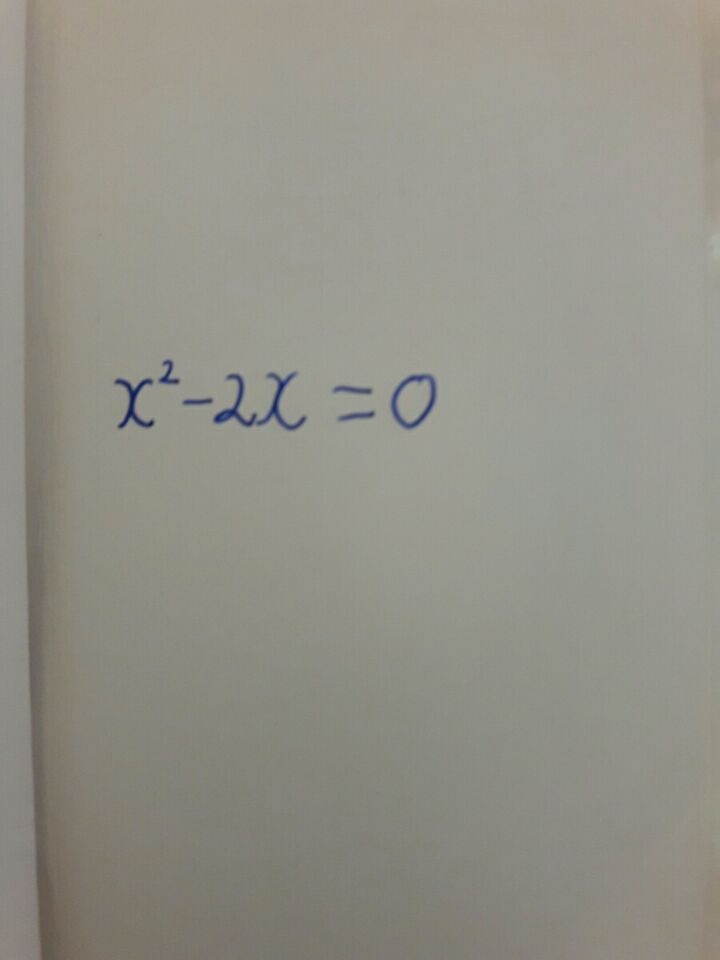 Theo dõi (0) 8 Trả lời
Theo dõi (0) 8 Trả lời -


Giải phương trình -0,4X²+1,2X=0
bởi Tuyêt's Ka
 15/04/2020
Giải phương trìnhTheo dõi (0) 1 Trả lời
15/04/2020
Giải phương trìnhTheo dõi (0) 1 Trả lời -


Tìm điều kiện để phương trình 2x^2-x+1+m=0 vô nghiệm
bởi Kiều's Thu's
 10/04/2020
Bài này làm thế nào
10/04/2020
Bài này làm thế nào Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm điều kiện m để phương trình x^2+x+2m=0 vô nghiệm
bởi Kiều's Thu's
 10/04/2020
10/04/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Các ac giúp e với
Các ac giúp e với Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm x biết 2x^2-5x=0
bởi Lê Thị Duy
 08/04/2020
08/04/2020
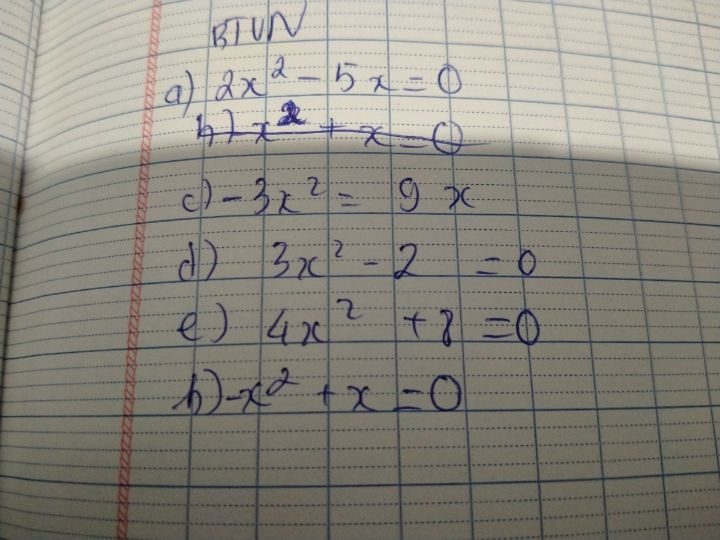 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -


Tìm m để phương trình x^2-2x-m=3 vô nghiệm
bởi Anh Nguyen
 31/03/2020
31/03/2020
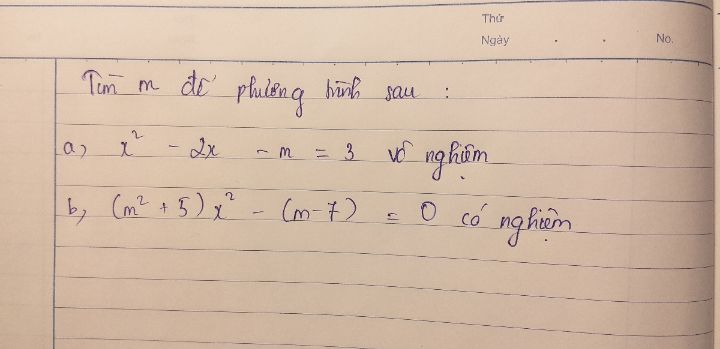 Theo dõi (1) 6 Trả lời
Theo dõi (1) 6 Trả lời -


Giải hệ phương trình 2x+y-5=0 và y+x^2=4x
bởi Diệp Trần
 31/03/2020
Cho phương trình sau
31/03/2020
Cho phương trình sau Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho phương trình ax^2+bx+c=0 (a khác 0). Chứng minh rằng nếu a+b+c=0 thì phương trình có 2 nghiệm x=1, x=c/a
bởi Hiền Diệu
 25/03/2020
25/03/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Viết phương trình đường thẳng d đi qua hai điểm
bởi San Nguyễn
 17/03/2020
Câu hai thôi
17/03/2020
Câu hai thôi Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Viết phương trình đường thẳng (d): y=ax+b, biết đường thẳng (d) song song với (d'): y=1÷2× x
bởi Be Hien Vo
 21/01/2020
viết phương trình đường thẳng (d): y=ax b, biết đường thẳng (d) song song với (d'): y=1÷2× x và cắt (P) tain điểm M có hoành độ là -2Theo dõi (0) 2 Trả lời
21/01/2020
viết phương trình đường thẳng (d): y=ax b, biết đường thẳng (d) song song với (d'): y=1÷2× x và cắt (P) tain điểm M có hoành độ là -2Theo dõi (0) 2 Trả lời -


Cho em hỏi với;
Một số bài toán về ứng dụng của phương trình bậc hai một ẩn trong đời sống.
em cảm ơn.
Theo dõi (0) 0 Trả lời -


Tìm GTNN của biểu thức A=x^2-3x+(4/x)+2016
bởi Trúc Đào
 20/12/2018
20/12/2018
Cho x>0. Tìm GTNN của biểu thức:
A=x^2-3x+(4/x)+2016
Theo dõi (1) 2 Trả lời -


Cho phương trình:
x²-2(m+3)x+2m-1=0
Tìm m để phương trình có 1 nghiệm là 2 và tìm nghiệm còn lại.
Theo dõi (0) 1 Trả lời -


Cho b và c là 2 số thỏa mãn hệ thức 1/b+1/c=1/2
bởi Suong dem
 03/01/2019
03/01/2019
cho b và c là 2 số thỏa mãn hệ thức : \(\dfrac{1}{b}+\dfrac{1}{c}=\dfrac{1}{2}\)
CMR: Trong 2 phuong trình sau phải có ít nhất 1 phương trình có nghiệm:
\(x^{2}+bx+c=0\) và \(x^{2}+cx+b=0\)Theo dõi (0) 1 Trả lời -


Giải phương trình x^2-3x-7=0
bởi Nguyễn Hiền
 07/01/2019
07/01/2019
\(x^2-3x-7=0\)
Theo dõi (0) 2 Trả lời -


Giải phương trình -2/5x^2-7/3x=0
bởi Đan Nguyên
 07/01/2019
07/01/2019
\(-\dfrac{2}{5}x^2-\dfrac{7}{3}x=0\)
Theo dõi (0) 1 Trả lời






