Phß║¦n hŲ░ß╗øng dß║½n giß║Żi b├Āi tß║Łp H├¼nh hß╗Źc 8 B├Āi 4 ─ÉŲ░ß╗Øng trung b├¼nh cß╗¦a tam gi├Īc, cß╗¦a h├¼nh thang sß║Į gi├║p c├Īc em nß║»m ─æŲ░ß╗Żc phŲ░ŲĪng ph├Īp v├Ā r├©n luyß╗ćn k─® n─āng, giß║Żi b├Āi tß║Łp tß╗½ SGK H├¼nh h├¼nh 8 Tß║Łp 1
-
B├Āi tß║Łp 20 trang 79 SGK To├Īn 8 Tß║Łp 1
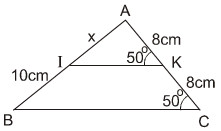
Tìm x trên hình 41.
-
B├Āi tß║Łp 21 trang 79 SGK To├Īn 8 Tß║Łp 1
T├Łnh khoß║Żng c├Īch AB giß╗»a hai m┼®i cß╗¦a compa tr├¬n h├¼nh 42, biß║┐t rß║▒ng C l├Ā trung ─æiß╗ām cß╗¦a OA, D l├Ā trung ─æiß╗ām cß╗¦a OB v├Ā OD = 3cm.

-
B├Āi tß║Łp 22 trang 80 SGK To├Īn 8 Tß║Łp 1
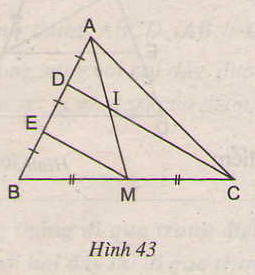
Cho h├¼nh 43. Chß╗®ng minh rß║▒ng AI = IM.
-
B├Āi tß║Łp 23 trang 80 SGK To├Īn 8 Tß║Łp 1
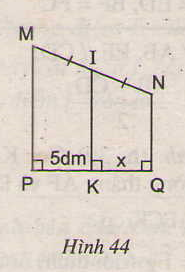
Tìm x trên hình 44,
-
B├Āi tß║Łp 24 trang 80 SGK To├Īn 8 Tß║Łp 1
Hai ─æiß╗ām A v├Ā B thuß╗Öc c├╣ng mß╗Öt nß╗Ła mß║Ęt phß║│ng c├│ bß╗Ø l├Ā ─æŲ░ß╗Øng xy. Khoß║Żng c├Īch tß╗½ ─æiß╗ām A ─æß║┐n xy bß║▒ng 12cm, khoß║Żng c├Īch tß╗½ ─æiß╗ām B ─æß║┐n xy bß║▒ng 20cm. T├Łnh khoß║Żng c├Īch tß╗½ trung ─æiß╗ām C cß╗¦a AB ─æß║┐n xy.
-
B├Āi tß║Łp 25 trang 80 SGK To├Īn 8 Tß║Łp 1
H├¼nh thang ABCD c├│ ─æ├Īy AB, CD. Gß╗Źi E, F, K theo thß╗® tß╗▒ l├Ā trung ─æiß╗ām cß╗¦a AD, BC, BD. Chß╗®ng minh ba ─æiß╗ām E, K, F thß║│ng h├Āng.
-
B├Āi tß║Łp 26 trang 80 SGK To├Īn 8 Tß║Łp 1
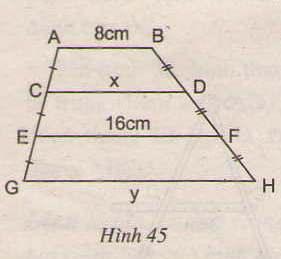
T├Łnh x, y tr├¬n h├¼nh 45, trong ─æ├│ AB // CD // EF // GH.
-
B├Āi tß║Łp 27 trang 80 SGK To├Īn 8 Tß║Łp 1
Cho tß╗® gi├Īc ABCD. Gß╗Źi E, F, K theo thß╗® tß╗▒ l├Ā trung ─æiß╗ām cß╗¦a AD, BC, AC.
a) So s├Īnh c├Īc ─æß╗Ö d├Āi EK v├Ā CD, KF v├Ā AB.
b) Chß╗®ng minh rß║▒ng \(EF \leq \frac{AB+CD}{2}\)
-
B├Āi tß║Łp 28 trang 80 SGK To├Īn 8 Tß║Łp 1
Cho h├¼nh thang ABCD (AB // CD), E l├Ā trung ─æiß╗ām cß╗¦a AD, F l├Ā trung ─æiß╗ām cß╗¦a BC. ─ÉŲ░ß╗Øng thß║▒ng EF cß║»t BD ß╗¤ I, cß║»t AC ß╗¤ K.
a) Chß╗®ng minh rß║▒ng AK = KC, BI = ID.
b) Cho AB = 6cm, CD = 10cm. T├Łnh c├Īc ─æß╗Ö d├Āi EI, KF, IK.
-
B├Āi tß║Łp 34 trang 84 SBT To├Īn 8 Tß║Łp 1
Cho tam gi├Īc ABC, ─æiß╗ām D thuß╗Öc cß║Īnh AC sao cho \(\displaystyle AD = {1 \over 2}DC\). Gß╗Źi M l├Ā trung ─æiß╗ām cß╗¦a BC, I l├Ā giao ─æiß╗ām cß╗¦a \(BD\) v├Ā \(AM.\) Chß╗®ng minh rß║▒ng \(AI = IM.\)
-
B├Āi tß║Łp 35 trang 84 SBT To├Īn 8 Tß║Łp 1
H├¼nh thang \(ABCD\) c├│ ─æ├Īy \(AB,\) \(CD.\) Gß╗Źi \(E, F, I\) theo thß╗® tß╗▒ l├Ā trung ─æiß╗ām cß╗¦a \(AD,\) \(BC,\) \(AC.\) Chß╗®ng minh rß║▒ng ba ─æiß╗ām \(E, I, F\) thß║│ng h├Āng.
-
B├Āi tß║Łp 36 trang 84 SBT To├Īn 8 Tß║Łp 1
Cho tß╗® gi├Īc ABCD. Gß╗Źi E, F, I theo thß╗® tß╗▒ l├Ā trung ─æiß╗ām cß╗¦a AD, BC, AC.
Chß╗®ng minh rß║▒ng:
a. EI// CD, IF // AB
b. \(EF \le {{AB + CD} \over 2}\)
-
B├Āi tß║Łp 37 trang 84 SBT To├Īn 8 Tß║Łp 1
Cho h├¼nh thang ABCD (AB // CD), M l├Ā trung ─æiß╗ām cß╗¦a AD, N l├Ā trung ─æiß╗ām cß╗¦a BC. Gß╗Źi I, K theo thß╗® tß╗▒ l├Ā giao ─æiß╗ām cß╗¦a MN vß╗øi BD, AC. Cho biß║┐t AB = 6cm,
CD = 14 cm. T├Łnh c├Īc ─æß╗Ö d├Āi MI, IK, KN.
-
B├Āi tß║Łp 38 trang 84 SBT To├Īn 8 Tß║Łp 1
Cho tam gi├Īc ABC, c├Īc ─æŲ░ß╗Øng trung tuyß║┐n BD v├Ā CE cß║»t nhau ß╗¤ G. Gß╗Źi I, K theo thß╗® tß╗▒ l├Ā trung ─æiß╗ām cß╗¦a GB, GC. Chß╗®ng minh rß║▒ng DE // IK, DE = IK.
-
B├Āi tß║Łp 39 trang 84 SBT To├Īn 8 Tß║Łp 1
Cho tam gi├Īc \(ABC,\) ─æŲ░ß╗Øng trung tuyß║┐n \(AM.\) Gß╗Źi \(D\) l├Ā trung ─æiß╗ām cß╗¦a \(AM,\) \(E\) l├Ā giao ─æiß╗ām cß╗¦a \(BD\) v├Ā \(AC.\) Chß╗®ng minh rß║▒ng \(AE = \displaystyle {1 \over 2}EC\).
-
B├Āi tß║Łp 40 trang 84 SBT To├Īn 8 Tß║Łp 1
Cho tam gi├Īc \(ABC,\) c├Īc ─æŲ░ß╗Øng trung tuyß║┐n \(BD,\) \(CE.\) Gß╗Źi \(M, N\) theo thß╗® tß╗▒ l├Ā trung ─æiß╗ām cß╗¦a \(BE, CD. \) Gß╗Źi \(I, K\) theo thß╗® tß╗▒ l├Ā giao ─æiß╗ām cß╗¦a \(MN\) vß╗øi \(BD, CE.\) Chß╗®ng minh rß║▒ng \(MI = IK = KN.\)
-
B├Āi tß║Łp 41 trang 84 SBT To├Īn 8 Tß║Łp 1
Chß╗®ng minh rß║▒ng ─æŲ░ß╗Øng thß║│ng ─æi qua trung ─æiß╗ām mß╗Öt cß║Īnh b├¬n cß╗¦a h├¼nh thang v├Ā song song vß╗øi hai ─æ├Īy th├¼ ─æi qua trung ─æiß╗ām cß╗¦a hai ─æŲ░ß╗Øng ch├®o v├Ā ─æi qua trung ─æiß╗ām cß╗¦a cß║Īnh b├¬n thß╗® hai.
-
B├Āi tß║Łp 42 trang 84 SBT To├Īn 8 Tß║Łp 1
Chß╗®ng minh rß║▒ng trong h├¼nh thang m├Ā hai ─æ├Īy kh├┤ng bß║▒ng nhau, ─æoß║Īn thß║│ng nß╗æi trung ─æiß╗ām cß╗¦a hai ─æŲ░ß╗Øng ch├®o bß║▒ng nß╗Ła hiß╗ću hai ─æ├Īy.
-
B├Āi tß║Łp 43 trang 85 SBT To├Īn 8 Tß║Łp 1
H├¼nh thang \(ABCD\) c├│ \(AB // CD,\) \(AB = a,\) \(BC = b,\) \(CD = c,\) \(DA = d.\) C├Īc ─æŲ░ß╗Øng ph├ón gi├Īc cß╗¦a c├Īc g├│c ngo├Āi ─æß╗ēnh \(A\) v├Ā \(D\) cß║»t nhau tß║Īi \(M,\) c├Īc ─æŲ░ß╗Øng ph├ón gi├Īc cß╗¦a c├Īc g├│c ngo├Āi ─æß╗ēnh \(B\) v├Ā \(C\) cß║»t nhau tß║Īi \(N.\)
\(a)\) Chß╗®ng ninh rß║▒ng \(MN // CD.\)
\(b)\) T├Łnh ─æß╗Ö d├Āi MN theo \(a, b, c, d\) (\(a, b, c, d\) c├│ c├╣ng ─æŲĪn vß╗ŗ ─æo)
-
B├Āi tß║Łp 44 trang 85 SBT To├Īn 8 Tß║Łp 1
Cho tam gi├Īc \(ABC,\) ─æŲ░ß╗Øng trung tuyß║┐n \(AM.\) Gß╗Źi \(O\) l├Ā trung ─æiß╗ām cß╗¦a \(AM.\) Qua \(O\) kß║╗ ─æŲ░ß╗Øng thß║│ng \(d\) cß║»t c├Īc cß║Īnh \(AB\) v├Ā \(AC.\) Gß╗Źi \(AAŌĆÖ, BBŌĆÖ, CCŌĆÖ\) l├Ā c├Īc ─æŲ░ß╗Øng vu├┤ng g├│c kß║╗ tß╗½ \(A, B, C\) ─æß║┐n ─æŲ░ß╗Øng thß║│ng \(d.\) Chß╗®ng minh rß║▒ng: \({{AA' = }}\displaystyle {{BB' + CC'} \over 2}\)
-
B├Āi tß║Łp 4.1 trang 85 SBT To├Īn 8 Tß║Łp 1
Tr├¬n h├¼nh \(bs.1,\) ta c├│ \(AB // CD // EF // GH\) v├Ā \(AC = CE = EG.\) Biß║┐t \(CD = 9,\) \(GH = 13.\) C├Īc ─æß╗Ö d├Āi \(AB\) v├Ā \(EF\) bß║▒ng:

\((A)\) \(8\) v├Ā \(10\)
\((B)\) \(6\) v├Ā \(12\)
\((C)\) \(7\) v├Ā \(11\)
\((D)\) \(7\) v├Ā \(12\)
-
B├Āi tß║Łp 4.2 trang 85 SBT To├Īn 8 Tß║Łp 1
Cho ─æŲ░ß╗Øng thß║│ng \(d\) v├Ā hai ─æiß╗ām \(A, B\) c├│ khoß║Żng c├Īch ─æß║┐n ─æŲ░ß╗Øng thß║│ng \(d\) theo thß╗® tß╗▒ l├Ā \(20cm\) v├Ā \(6cm.\) Gß╗Źi \(C\) l├Ā trung ─æiß╗ām cß╗¦a \(AB.\) T├Łnh khoß║Żng c├Īch tß╗½ \(C\) ─æß║┐n ─æŲ░ß╗Øng thß║│ng \(d.\)
-
B├Āi tß║Łp 4.3 trang 85 SBT To├Īn 8 Tß║Łp 1
Cho tam gi├Īc \(ABC.\) Gß╗Źi \(M\) l├Ā trung ─æiß╗ām cß╗¦a \(BC.\) Tr├¬n tia ─æß╗æi cß╗¦a tia \(BA\) lß║źy ─æiß╗ām \(D\) sao cho \(BD = AB.\) Gß╗Źi \(K\) l├Ā giao ─æiß╗ām cß╗¦a \(DM\) v├Ā \(AC.\) Chß╗®ng minh rß║▒ng \(AK = 2KC.\)






