Bài tập 41 trang 84 SBT Toán 8 Tập 1

Hướng dẫn giải

+) Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.

+) Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.

Lời giải chi tiết

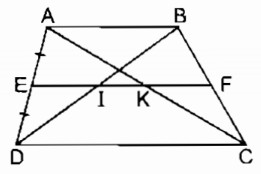
Xét hình thang \(ABCD\) có: \(AB // CD.\)

\(E\) là trung điểm của \(AD,\) đường thẳng đi qua \(E\) song song với \(AB\) cắt \(BC\) tại \(F,\) \(AC\) tại \(K,\) \(BD \) tại \(I.\)

Vì \(E\) là trung điểm của \(AD\)

\(EF // AB\)

Suy ra: \(BF = FC\) (tính chất đường trung bình hình thang)

+) Ta có \(EK//AB\) và \(AB//CD\) nên \(EK//DC\)

Trong tam giác \(ADC\) ta có:

\(E\) là trung điểm của \(AD\)

\(EK // DC\)

Suy ra: \(AK = KC\) (tính chất đường trung bình tam giác)

Trong tam giác \(ABD\) ta có:

\(E\) là trung điểm cạnh \(AD\)
\(EI // AB\)

Suy ra: \(BI = ID\) (tính chất đường trung bình của tam giác)

Vậy đường thẳng đi qua trung điểm \(E\) của cạnh bên \(AD\) của hình thang \(ABCD\) thì đi qua trung điểm cạnh bên \(BC\) và trung điểm hai đường chéo \(AC, BD.\

-- Mod Toán 8 HỌC247