Giải bài 39 tr 84 sách BT Toán lớp 8 Tập 1
Cho tam giác \(ABC,\) đường trung tuyến \(AM.\) Gọi \(D\) là trung điểm của \(AM,\) \(E\) là giao điểm của \(BD\) và \(AC.\) Chứng minh rằng \(AE = \displaystyle {1 \over 2}EC\).
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng định nghĩa, tính chất đường trung bình của tam giác:
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
+) Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
Lời giải chi tiết
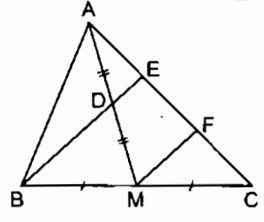
Gọi F là trung điểm của EC
Trong ∆ CBE ta có:
M là trung điểm của cạnh CB
F là trung điểm của cạnh CE
Nên MF là đường trung bình của ∆ CBE
⇒ MF // BE (tính chất đường trung bình của tam giác)
Hay DE // MF
Trong tam giác AMF ta có:
D là trung điểm của AM
DE // MF
Suy ra: AE = EF (tính chất đường trung bình của tam giác)
Mà \(EF = FC = {{EC} \over 2}\0 nên \(AE = {1 \over 2}EC\).
-- Mod Toán 8 HỌC247
-


Bài 22 trang 80 SGK Toán 8
bởi Van Tho
 22/09/2018
22/09/2018
bài 22 trong sách giáo khoa lop 8 trang 80
Theo dõi (0) 1 Trả lời -


Chứng minh CD=4MD biết tam giác ABC cân tại A có M là trung điểm của đường cao AH
bởi Mai Hoa
 29/03/2019
29/03/2019
Bài 1: Cho tam giác ABC,trên nửa mặt phẳng bờ là AC không chứa điểm B.Lấy điểm D bất kì.Gọi M,N,P,Q lần lượt là trung điểm của AB,AC,CD,AD
1)Chứng minh: MN//PQ và MQ//NP
2)Chứng minh: MN+NP+PQ+MQ=AC+BD
Bài 2: Cho tam giác ABC cân tại A có M là trung điểm của đường cao AH,đường thẳng CM cắt AB tại D.Kẻ Hx//CD và cắt AB tại E
1)Chứng minh: DA=DE
2)Chứng minh: AB=3AD
3)Chứng minh: CD=4MD
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC, gọi M, N lần lượt là trung điểm của AC và AB. Trên tia đối của tia MB lấy điểm D sao cho MD = MB, trên tia đối của tia NC lấy điểm E sao cho NE = NC. Chứng minh
a) AD = BC ; AD // BC
b) AD = AE
c) E, A, D thẳng hảng
Theo dõi (0) 1 Trả lời -


Chứng minh FE=BC/2 biết tam giác ABC có D là trung điểm của AB, E trung điểm AC
bởi Trần Thị Trang
 06/04/2019
06/04/2019
Cho ΔABC, D là trung điểm của AB, E là trung điểm của AC. Trên tia đối của tia ED lấy điểm F sao cho EF=ED. Chứng minh:
a) ΔAED=ΔCEF
b)AB//FC
c) FE=\(\dfrac{BC}{2}\)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 37 trang 84 SBT Toán 8 Tập 1
Bài tập 38 trang 84 SBT Toán 8 Tập 1
Bài tập 40 trang 84 SBT Toán 8 Tập 1
Bài tập 41 trang 84 SBT Toán 8 Tập 1
Bài tập 42 trang 84 SBT Toán 8 Tập 1
Bài tập 43 trang 85 SBT Toán 8 Tập 1
Bài tập 44 trang 85 SBT Toán 8 Tập 1
Bài tập 4.1 trang 85 SBT Toán 8 Tập 1






