Giải bài 36 tr 84 sách BT Toán lớp 8 Tập 1
Cho tứ giác ABCD. Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC.
Chứng minh rằng:
a. EI// CD, IF // AB
b. \(EF \le {{AB + CD} \over 2}\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
\(a)\) Sử dụng định nghĩa, tính chất đường trung bình của tam giác:
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
\(b)\) Sử dụng bất đẳng thức tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.
Lời giải chi tiết
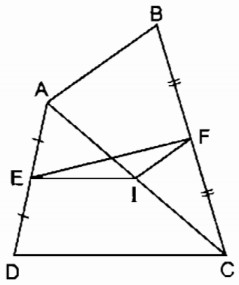
a) Trong tam giác ADC, ta có:
E là trung điểm của AD (gt)
I là trung điểm của AC (gt)
Nên EI là đường trung bình của ∆ ABC
⇒ EI // CD (tính chất đường trung bình của tam giác)
Và \(EI = {{CD} \over 2}\)
Trong tam giác ABC ta có:
I là trung điểm của AC
F là trung điểm của BC
Nên IF là đường trung bình của ∆ ABC
⇒ IF // AB (tính chất đường trung bình của tam giác)
Và \(IF = {{AB} \over 2}\)
b) Trong ∆ EIF ta có: EF ≤ EI + IF (dấu “=” xảy ra khi E, I, F thẳng hàng)
Mà \(EI = {{CD} \over 2}{\rm{;}}\,\,IF{\rm{ = }}{{AB} \over 2}\) (chứng minh trên) \( \Rightarrow {\rm{EF}} \le {{CD} \over 2} + {{AB} \over 2}\)
Vậy \(EF \le {{AB + CD} \over 2}\) (dấu bằng xảy ra khi AB // CD)
-- Mod Toán 8 HỌC247
-

 Cần gấp
Cần gấp Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Nêu tính chất đương trung bình của tam giác?
bởi Bạch Nương
 17/04/2020
17/04/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm x, y trong các hình vẽ
bởi Ha Nguyen
 15/04/2020
15/04/2020
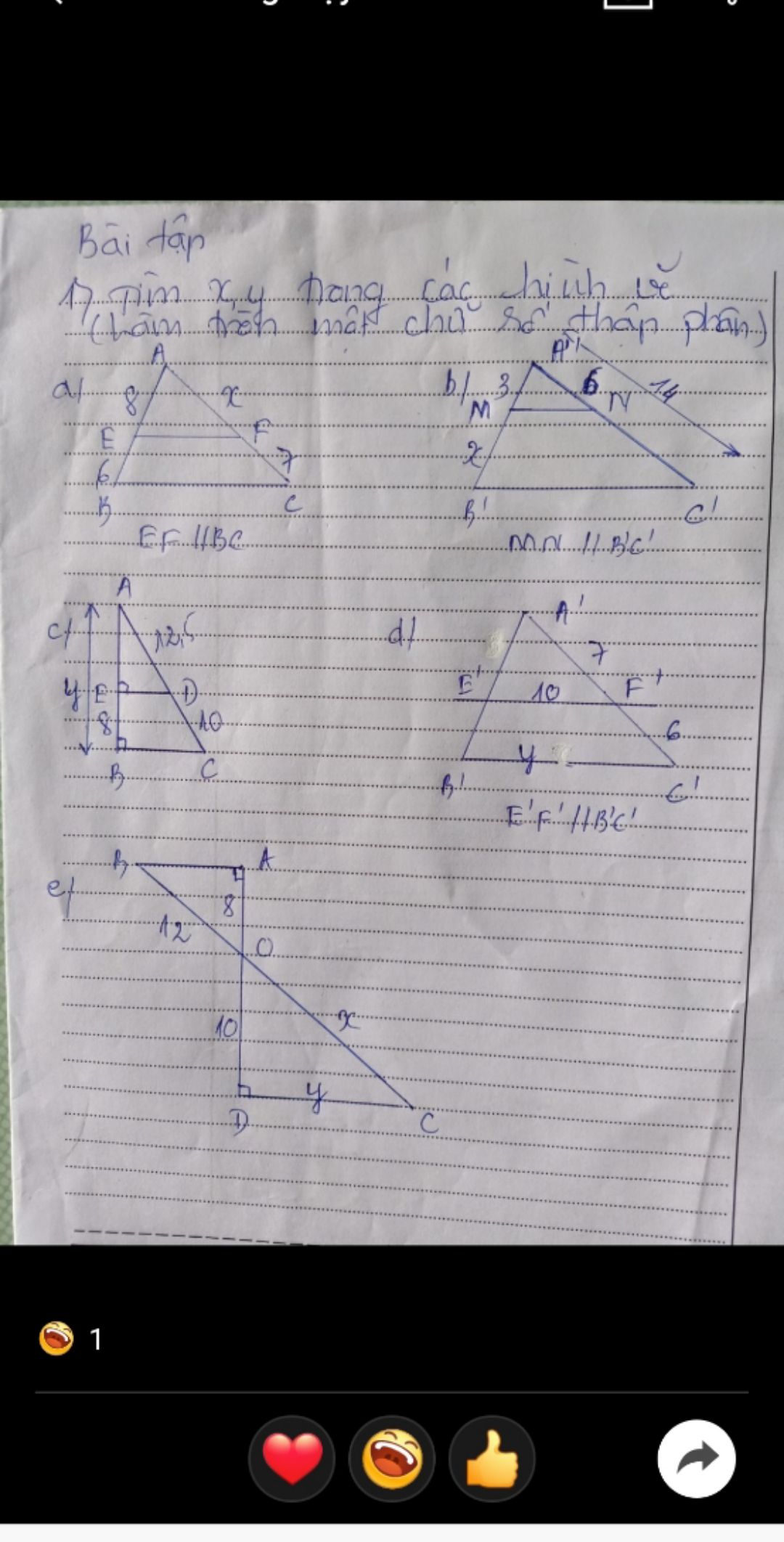 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


3a
 Theo dõi (1) 7 Trả lời
Theo dõi (1) 7 Trả lời
Bài tập SGK khác
Bài tập 34 trang 84 SBT Toán 8 Tập 1
Bài tập 35 trang 84 SBT Toán 8 Tập 1
Bài tập 37 trang 84 SBT Toán 8 Tập 1
Bài tập 38 trang 84 SBT Toán 8 Tập 1
Bài tập 39 trang 84 SBT Toán 8 Tập 1
Bài tập 40 trang 84 SBT Toán 8 Tập 1
Bài tập 41 trang 84 SBT Toán 8 Tập 1
Bài tập 42 trang 84 SBT Toán 8 Tập 1
Bài tập 43 trang 85 SBT Toán 8 Tập 1
Bài tập 44 trang 85 SBT Toán 8 Tập 1
Bài tập 4.1 trang 85 SBT Toán 8 Tập 1






