Giải bài 27 tr 80 sách GK Toán 8 Tập 1
Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC.
a) So sánh các độ dài EK và CD, KF và AB.
b) Chứng minh rằng \(EF \leq \frac{AB+CD}{2}\)
Hướng dẫn giải chi tiết
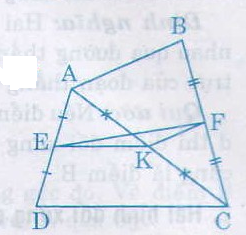
a) Xét \(∆ACD\) có \(E, K\) theo thứ tự là trung điểm của \(AD, AC\) (giả thiết)
\(\Rightarrow EK\) là đường trung bình của \(∆ACD\) (dấu hiệu nhận biết đường trung bình của tam giác)
\(\Rightarrow EK = \dfrac{CD}{2}\) (tính chất đường trung bình của tam giác).
- Xét \(∆ABC\) có \(K, F\) theo thứ tự là trung điểm của \(AC, BC\) (giả thiết)
\(\Rightarrow FK\) là đường trung bình của \(∆ABC\) (dấu hiệu nhận biết đường trung bình của tam giác)
\(\Rightarrow KF = \dfrac{AB}{2}\) (tính chất đường trung bình của tam giác).
b) TH1: Ba điểm \(E, K, F\) không thẳng hàng
Xét \(\Delta EFK\) có: \(EF < EK + KF\) (bất đẳng thức tam giác)
Nên \(EF < EK + KF = \dfrac{CD}{2} + \dfrac{AB}{2} \)\(\,= \dfrac{AB+CD}{2}\)
Hay \(EF < \dfrac{AB+CD}{2}\) (1)
TH2: Ba điểm \(E, K, F\) thẳng hàng
Khi đó: \(EF = EK + KF = \dfrac{CD}{2} + \dfrac{AB}{2} \)\(\,= \dfrac{AB+CD}{2}\)
Hay \(EF = \dfrac{AB+CD}{2}\) (2)
Từ (1) và (2) suy ra \(EF \le \dfrac{AB+CD}{2}\).
-- Mod Toán 8 HỌC247
-


Hãy chọn câu đúng? Cho ΔABC, I, K lần lượt là trung điểm của AB và AC. Biết BC = 8 cm, AC = 7cm. Ta có:
bởi Mai Rừng
 15/01/2021
15/01/2021
A. IK = 4cm
B. IK = 4,5 cm
C. IK = 3,5cm
D. IK = 14cm
Theo dõi (0) 1 Trả lời -


Một hình thang có đáy lớn là 8 cm, đáy nhỏ ngắn hơn đáy lớn là 2 cm. Độ dài đường trung bình của hình thang là:
bởi Phạm Hoàng Thị Trà Giang
 15/01/2021
15/01/2021
A. 5,5 cm
B. 5 cm
C. 6 cm
D. 7 cm
Theo dõi (0) 1 Trả lời -


Một hình thang có đáy lớn là 5 cm, đáy nhỏ ngắn hơn đáy lớn là 0,8 cm. Độ dài đường trung bình của hình thang là:
bởi sap sua
 15/01/2021
15/01/2021
A. 4,7 cm
B. 4,8 cm
C. 4,6 cm
D. 5 cm
Theo dõi (0) 1 Trả lời -


Hãy chọn câu đúng? Cho tam giác ABC có chu vi 80. Gọi E, F, P là trung điểm của các cạnh AB, BC, CA. Chu vi của tam giác EFP là:
bởi Mai Trang
 16/01/2021
16/01/2021
A. 40 cm
B. 20 cm
C. 45 cm
D. 50 cm
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 25 trang 80 SGK Toán 8 Tập 1
Bài tập 26 trang 80 SGK Toán 8 Tập 1
Bài tập 28 trang 80 SGK Toán 8 Tập 1
Bài tập 34 trang 84 SBT Toán 8 Tập 1
Bài tập 35 trang 84 SBT Toán 8 Tập 1
Bài tập 36 trang 84 SBT Toán 8 Tập 1
Bài tập 37 trang 84 SBT Toán 8 Tập 1
Bài tập 38 trang 84 SBT Toán 8 Tập 1
Bài tập 39 trang 84 SBT Toán 8 Tập 1
Bài tập 40 trang 84 SBT Toán 8 Tập 1
Bài tập 41 trang 84 SBT Toán 8 Tập 1
Bài tập 42 trang 84 SBT Toán 8 Tập 1
Bài tập 43 trang 85 SBT Toán 8 Tập 1
Bài tập 44 trang 85 SBT Toán 8 Tập 1
Bài tập 4.1 trang 85 SBT Toán 8 Tập 1





