Bài tập 43 trang 85 SBT Toán 8 Tập 1

Hướng dẫn giải

+) Trong tam giác cân, đường phân giác ứng với cạnh đáy cũng là đường trung tuyến.

+) Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.

+) Đường trung bình của hình thang thì song song với hai cạnh đáy và bằng nửa tổng hai đáy.

Lời giải chi tiết

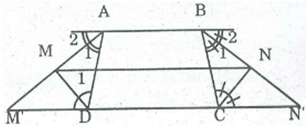
\(a)\) Gọi \(M’\) và \(N’\) là giao điểm của tia \(AM\) và \(BN\) với \(CD.\)

Vì ABCD là hình thang nên \(AB//CD\) hay \(AB//M'N'\)

Suy ra \(ABN'M'\) cũng là hình thang.

Ta có:

Vì \(AB//M'N'\) nên \(\widehat {M'} = {\widehat A_2}\) (hai góc so le trong)

\({\widehat A_1} = {\widehat A_2}\) (do AM' là phân giác góc ngoài tại đỉnh A)

Suy ra: \(\widehat {M'} = {\widehat A_1}\) 

Nên \(∆ ADM’\) cân tại \(D\)

Có \(DM\) là phân giác của \(\widehat {ADM'}\) 

Suy ra: \(DM\) là đường trung tuyến (tính chất tam giác cân)

\(⇒ AM = MM’\) (1)

Vì \(AB//M'N'\) nên \(\widehat {N'} = {\widehat B_2}\) (hai góc so le trong)

\({\widehat B_1} = {\widehat B_2}\) (do BN' là phân giác góc ngoài tại đỉnh B)

Suy ra: \(\widehat {N'} = {\widehat B_1}\) 

Nên \(∆ BCN’\) cân tại \(C\)

Có \(CN\) là phân giác của \(\widehat {BCN'}\)

Suy ra: \(CN\) là đường trung tuyến (tính chất tam giác cân)

\(⇒ BN = NN’\) (2)

Từ (1) và (2) suy ra: \(MN\) là đường trung bình của hình thang \(ABN’M’\)

\(⇒ MN // M’N’\) (tính chất đường trung bình hình thang)

Hay \(MN // CD\)

\(b)\) \(MN =\displaystyle  {{AB + M'N'} \over 2}\) (tính chất đường trung bình của hình thang)

\( \Rightarrow MN = \displaystyle  {{AB + M'D + CD + CN'} \over 2}\;\,( * )\)

Mà \(M’D = AD\) (vì \(∆ ADM’\) cân tại \(D\)) và \(CN’ = BC\) (vì \(∆ BCN’\) cân tại \(C\))

Thay vào \((*)\) ta được: 

\(MN = \displaystyle  {{AB + AD + CD + BC} \over 2}\)\( = \displaystyle {{a + d + c + b} \over 2}\)

-- Mod Toán 8 HỌC247