Bài tập 49 trang 84 SGK Toán 8 Tập 2

Lý thuyết10 Trắc nghiệm

17 BT SGK

120 FAQ

Giải bài 49 tr 84 sách GK Toán 8 Tập 2

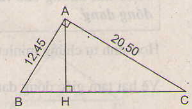
Ở hình 51, tam giác ABC vuông tại A có đường cao AH

a) Trong hình vẽ có bao nhiêu cặp tam giác đồng dạng?.

b) Cho biết: AB = 12,45 cm, AC = 20,50cm. Tính độ dài các đoạn BC, AH, BH và CH.

Hình 51 bài 49 trang 84 SGK Toán 8 Tập 2

Hình học 8 Chương 3 Bài 8 Trắc nghiệm Hình học 8 Chương 3 Bài 8 Giải bài tập Hình học 8 Chương 3 Bài 8

Hướng dẫn giải chi tiết

Câu a:

Xét $∆ABC $ và $ ∆HBA$ có:

$\widehat{A} = \widehat{H}={90^o}$

$\widehat{B}$ chung

$\Rightarrow ∆ABC ∽ ∆HBA$ (1) (g-g)

Xét $∆ABC $ và $ ∆HAC$ có:

$\widehat{A} = \widehat{H}={90^o}$

$\widehat{C}$ chung

$\Rightarrow ∆ABC ∽ ∆HAC$ (2) (g-g)

Từ (1) và (2) suy ra $∆HAC ∽ ∆HBA$ (vì cùng đồng dạng với $∆ABC$)

Vậy trong hình vẽ có 3 cặp tam giác đồng dạng

Câu b:

$∆ABC$ vuông tại $A$ (giả thiết) nên áp dụng định lí Pitago ta có:

$\eqalign{
& B{C^2} = A{B^2} + A{C^2} \cr
& \;\;\;\;\;\;\;\;= 12,{45^2} + 20,{50^2} = 575,2525 \cr
& \Rightarrow BC = \sqrt {575,2525} \approx 24\,cm \cr} $

$∆ABC ∽ ∆HBA $ (chứng minh trên)

$\Rightarrow \dfrac{AB}{HB} = \dfrac{BC}{BA}$ ( cặp cạnh tương ứng tỉ lệ)

$\Rightarrow HB = \dfrac{AB^{2}}{BC} ≈ \dfrac{12,45^{2}}{24}≈ 6,5 cm$

$\Rightarrow CH = BC - BH \approx 24 - 6,5 $$\,= 17,5 cm.$

Mặt khác: $\dfrac{AC}{AH} = \dfrac{BC}{BA}$ (do $∆ABC ∽ ∆HBA$ theo câu a)

$\Rightarrow AH = \dfrac{AB.AC}{BC} \approx \dfrac{12,45.20,50}{24}$

$\Rightarrow AH \approx 10,6 cm$.

-- Mod Toán 8 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 49 trang 84 SGK Toán 8 Tập 2 HAY thì click chia sẻ

YOMEDIA

Chứng minh tứ giác MNHP là hình thang cân?

bởi Gia Khánh 13/08/2020

BÀI 1: Cho tam giác ABC có AB bé hơn AC . Đường cao AH . Gọi M,N,P lần lượt là là trung điểm của AB,AC,BC

a. Chứng minh tứ giác MNHP là hình thang cân

b. Gọi I là giao điểm của MH,PN . Chứng minh I cách đều MN

BÀI 2: cho tam giác ABC. Các đường trung tuyến BD,CE cắt nhau tại G . Gọi I,K theo thứ tự là trung điểm của BG và CG

a. Tứ giác BEDC là hình gì ? Vì sao?

b Chứng minh ED=IK,ED//IK,EI//DK

c. Tam giác ABC cần điều kiện gì để tứ giác BDEC là hình thang ?

Theo dõi (0) 8 Trả lời
Chứng minh CA là phân giác của góc C?

bởi Hương Lan 12/08/2020

Cho hình thang ABCD (AB//CD), AB=CD

a) Chứng minh CA là phân giác của góc C.

b) Vẽ AE//BC , E thuộc CD. Chứng minh AC là trung trực của BE; BE là trung trực của AC.

Theo dõi (0) 1 Trả lời
Tính độ dài BM?

bởi Lương Tiểu Băng 05/08/2020
Hình thang $A B C D$ có cạnh đáy $A B$ dài $8 c m$ , cạnh đáy dài $12 c m$ . Điểm nằm trên đường thẳng sao cho đường thẳng $D M$ chia hình thang thành hai phần có diện tích bằng nhau. Tính độ dài $B M$ .
Theo dõi (2) 11 Trả lời
Cho tam giác ABC nhọn, H là trực tâm, CMR: $\frac{{BH.CH}}{{AB.AC}} + \frac{{CH.AH}}{{BC.BA}} + \frac{{AH.BH}}{{CA.CB}} = 1$?

bởi Army 23/07/2020

Hình 8, tam giác đồng dạng,bài 16

Theo dõi (0) 0 Trả lời
Chứng minh $\Delta ABC$ đồng dạng $\Delta HBA$?

bởi 佐藤みちお 05/07/2020

Theo dõi (0) 1 Trả lời
Chứng minh tam giác ADI cân?

bởi Hổ Bạch 30/06/2020

Bạn nào giúp mik bài 4 ý c vs ạ

Theo dõi (0) 1 Trả lời
Chứng minh rằng AO^2=AC.BD?

bởi Ngô Thị Yến Nhi 29/06/2020

Cho đoạn thẳng AB và trung điểm O thuộc đoạn thẳng đó . Vẽ tia Ax và By lần lượt vuông góc với AB tại A và B. Lấy C thuộc tia Ax, vẽ tia Om vuông góc với OC tại O, Om cắt tia By tại D.

a) CMR: AO² = AC.BD

b) CMR: △ACO đồng dạng với tam giác △OCD.

Theo dõi (1) 4 Trả lời
Chứng minh tam giác BDC đồng dạng với tam giác AHB?

bởi Thu Thuỷ 27/06/2020

Giải hộ mk vs ạ

Theo dõi (0) 2 Trả lời