Giải bài 50 tr 96 sách BT Toán lớp 8 Tập 2
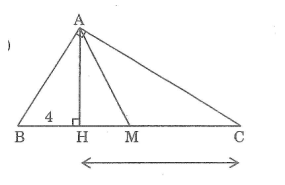
Tam giác vuông ABC (A = 90o) có đường cao AH và trung tuyến AM. Tính diện tích tam giác AMH,biết rằng BH = 4cm, CH = 9cm
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
- Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
Lời giải chi tiết
Xét hai tam giác vuông \(HBA\) và \(HAC\) có:
\(\widehat {BHA} = \widehat {AHC} = 90^\circ \)
\(\widehat {HBA} = \widehat {HAC}\) (vì hai góc cùng phụ với \(\widehat C\))
\( \Rightarrow ∆ HBA \backsim ∆ HAC\) (g.g)
\( \Rightarrow \displaystyle {{HA} \over {HB}} = {{HC} \over {HA}}\)
\( \Rightarrow H{A^2} = HB.HC = 4.9 = 36\)
\( \Rightarrow AH = 6\;(cm)\).
Vì \(AM\) là trung tuyến nên \(M\) là trung điểm của \(BC\) do đó \(\displaystyle BM = {1 \over 2}BC = {1 \over 2}.\left( {9 + 4} \right) \)\(\,=6,5\; (cm)\)
Mà \(HM = BM - BH = 6,5 - 4 \)\(\,= 2,5\; (cm)\).
Vậy \(\displaystyle {S_{AHM}} = {1 \over 2}AH.HM = {1 \over 2}.6.2,5 \)\(\,= 7,5\,(c{m^2})\).
-- Mod Toán 8 HỌC247
-
Bài 50 trang 96 sách bài tập toán 8 tập 2
bởi bach hao
11/10/2018
Bài 50 (Sách bài tập - tập 2 - trang 96)
Tam giác vuông ABC (\(\widehat{A}=90^0\)) có đường cao AH và trung tuyến AM (h.36).
.jpg)
Tính diện tích tam giác AMH, biết BH = 4cm, CH = 9cm ?
Theo dõi (0) 1 Trả lời -
Bài 49 trang 96 sách bài tập toán 8 tập 2
bởi Đan Nguyên
11/10/2018
Bài 49 (Sách bài tập - tập 2 - trang 96)
Đường cao của một tam giác vuông xuất phát từ đỉnh góc vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 9cm và 16 cm.
.jpg)
Tính độ dài các cạnh của tam giác vuông đó (h.35) ?
Theo dõi (0) 1 Trả lời -
Bài 48 trang 95 sách bài tập toán 8 tập 2
bởi Mai Rừng
29/09/2018
Bài 48 (Sách bài tập - tập 2 - trang 95)Cho tam giác ABC (\(\widehat{A}=90^0\)) có đường cao AH (h.34).
Chứng minh rằng : \(AH^2=BH.CH\)
Theo dõi (0) 1 Trả lời -
Bài 47 trang 95 sách bài tập toán 8 tập 2
bởi na na
11/10/2018
Bài 47 (Sách bài tập - tập 2 - trang 95)
.jpg)
Trên hình 33 hãy chỉ ra các tam giác đồng dạng. Viết các cặp tam giác đồng dạng theo thứ tự các đỉnh tương ứng và giải thích vì sao chúng đồng dạng ?
Theo dõi (0) 1 Trả lời -
Bài 46 trang 95 sách bài tập toán 8 tập 2
bởi Nguyễn Quang Minh Tú
29/09/2018
Bài 46 (Sách bài tập - tập 2 - trang 95)Cho tam giác ABC vuông tại A, AC = 4cm, BC = 6 cm. Kẻ tia Cx vuông góc với BC (Tia Cx và điểm A khác phía so với đường thẳng BC). Lấy trên tia Cx điểm D sao cho BD = 9cm (h.32).
Chứng minh rằng : BD // AC
Theo dõi (0) 1 Trả lời -
Bài 45 trang 95 sách bài tập toán 8 tập 2
bởi Lê Gia Bảo
11/10/2018
Bài 45 (Sách bài tập - tập 2 - trang 95)
Cho hình thang vuông ABCD ( \(\widehat{A}=\widehat{D}=90^0\)), AB = 6cm, CD = 12cm, AD = 17cm. Trên canh AD, đặt đoạn thắng AE = 8cm (h.31).
.jpg)
Chứng minh :
\(\widehat{BEC}=90^0\)
Theo dõi (0) 1 Trả lời -
Bài 44 trang 95 sách bài tập toán 8 tập 2
bởi Nguyễn Thanh Trà
11/10/2018
Bài 44 (Sách bài tập - tập 2 - trang 95)
Cho tam giác ABC vuông tại A, AC = 9cm, BC = 24cm. Đường trung trực của BC cắt đường thẳng AC tại D, cắt BC tại M (h.30).
.jpg)
Tính độ dài của đoạn thẳng CD ?
Theo dõi (0) 1 Trả lời -
Chứng minh tam giác ABC =ADC
bởi Nguyễn Thị Thu Huệ
31/05/2019
cho tam giác ABC vuông tại A có AB=5cm AC=12cm
tính BC
trên tia đối của AB lấy D sao cho AB=AD.chúng minh 2 tam giác ABC =ADC
đường thẳng a https:https://hoc247.net/image/faq/data2/216985_.https://hoc247.net/image/faq/data2/216985_.hoc247.nethttps://hoc247.net/image/faq/data2/216985_.imagehttps://hoc247.net/image/faq/data2/216985_.faqhttps://hoc247.net/image/faq/data2/216985_.data2https://hoc247.net/image/faq/data2/216985_.563596_.https:https://hoc247.net/image/faq/data2/216985_.https://hoc247.net/image/faq/data2/216985_.hoc247.nethttps://hoc247.net/image/faq/data2/216985_.imagehttps://hoc247.net/image/faq/data2/216985_.faqhttps://hoc247.net/image/faq/data2/216985_.data2https://hoc247.net/image/faq/data2/216985_.563596_. BC cắt CD tại E.chứng minh tam giác EAC cân
gọi F là trung điểm của BC.chứng minh CA,DF,BE đồng quy tại 1 điểm
Theo dõi (0) 1 Trả lời
