Giải bài 48 tr 95 sách BT Toán lớp 8 Tập 2
Cho tam giác \(ABC\) (\(\widehat A = 90^\circ \)) có đường cao \(AH\) (h.34)
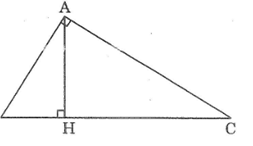
Chứng minh rằng \(A{H^2} = BH.CH\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
- Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng. Từ đó suy ra hệ thức về cạnh.
- Hai góc cùng phụ với một góc thứ ba thì bằng nhau.
Lời giải chi tiết
Xét tam giác \(ABC\) vuông tại \(A\) nên \(\widehat {CBA} + \widehat {ACB} = 90^\circ \)
Xét tam giác \(AHC\) vuông tại \(H\) nên \(\widehat {HAC} + \widehat {ACH} = 90^\circ \)
Suy ra \(\widehat {HBA} = \widehat {HAC}\) (hai góc cùng phụ với \(\widehat {ACB}\))
Xét hai tam giác vuông \(HBA\) và \(HAC\) có:
\(\widehat {BHA} = \widehat {AHC} = 90^\circ \)
\(\widehat {HBA} = \widehat {HAC}\) (chứng minh trên)
\( \Rightarrow ∆ HBA \backsim ∆ HAC\) (g.g)
\( \Rightarrow\displaystyle {{HA} \over {HB}} = {{HC} \over {HA}}\)
\( \Rightarrow A{H^2} = HB.HC\) (đpcm)
-- Mod Toán 8 HỌC247
-


Chứng minh tam giác ADE đồng dạng tam giác ACB
bởi Nguyễn Thanh Thảo
 31/05/2019
31/05/2019
Cho tam giac ABC
co AB=6cm ; AC=4cm, tren canh AB lay diem D , tren canh AC lay diem E sao cho AD= 2cm ; AE = 3cm
a) Chung minh tam giac ADE dong giang vs tam giac ACB
b) biet tam giac co dien tich la S , tinh die tich tam giac ADETheo dõi (0) 1 Trả lời -


Cho tam giác nhọn ABC ( góc A < 90° ) kẻ BD vuông góc với AC tại F , CE vuông góc với AB tại E , BD cắt CE tại H . chứng minh ;
a) tam giác AEC đồng dạng với tam giác ADB , từ đó suy ra AE.AB=AD.AC
b) tam giác DHC đồng dạng với tam giác EHB
c) AH cắt BC tại F . cm tam giác AFC đồng dạng với tam giác BDC
d) BE.BA+CD.CA= BC bình
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm. Vẽ đường cao AH.
a) Tính BC.
b) Chứng minh AB2= BH.BC
c) Vẽ phân giác AD của góc A ( D\(\in\) BC). Chứng minh H nằm giữa B và D.
Theo dõi (0) 1 Trả lời -


Chứng minh tứ giác AIHK là hình chữ nhật
bởi het roi
 31/05/2019
31/05/2019
Cho tam giác ABC vuông tại A, đường cao AH. Biết BH=4cm, CH=9cm. Gọi I và K lần lượt là hình chiếu của H lên AB và AC
a. Chứng minh tứ giác AIHK là hình chữ nhật
b. Cm tam giác AKI đồng dạng với tam giác ABC
c. Tính diện tích của tam giác ABC
Help me
Làm phần c cho mình nhé
Theo dõi (0) 1 Trả lời -


Chứng minh BC^2 = BH . BD + CH . CE
bởi Mai Trang
 31/05/2019
31/05/2019
Cho tam giác nhọn ABC, các đường cao BD, CE cắt nhau tại H. C/m: BC2 = BH . BD + CH . CE
Theo dõi (0) 1 Trả lời -


Tính diện tích AED
bởi Nguyễn Hồng Tiến
 31/05/2019
31/05/2019
Cho tam giác ABC vuông tại A có AB=30cm, AC=40cm. Kẻ AH vuông góc BC (H∈∈BC).
a) CM: ΔABC∼ΔHBAΔABC∼ΔHBA
b) Từ H kẻ HD⊥⊥ AB, HE⊥AC⊥AC (D∈AB, E ∈ AC)
AH2= AD.AB và AH2=AE.AC
c) Tính diện tích ΔΔAED?
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác AEF đồng dạng với tam giác CED từ đó suy ra tia EH là pg của góc EFD
bởi Hoa Hong
 31/05/2019
31/05/2019
cho tam giác ABC có 3 góc nhọn , hai đường cao BE , CF cắt nhau tại H.
a)C/M: AH vuông góc với BC
b) Chứng tỏ AE.AC=AF.AB
C) C/M tam giác AEF đồng dạng với tam giác ABC
d) C/M: tam giác AEF đồng dạng với tam giác CED từ đó suy ra tia EH là pg của góc EFD
mk cần gấp các bn giúp mk nhé
các bn giải như một bài giải đầy đủ hộ mk nhé
Theo dõi (0) 1 Trả lời -


Tính độ dài đoạn thẳng BC và CD
bởi thu hằng
 31/05/2019
31/05/2019
Cho tam giác ABC vuông tại A có AB=6cm,AC=8cm,đường cao AH,tia phân giác của góc A cắt BC tại D
a)Tính độ dài đoạn thẳng BC và CD?
b)Tính chiều cao AH của tam giác ABC
c)Lấy điểm E sao cho tứ giác ADCE là hình bình hành.Kẻ EM vuông góc với AC(M thuộc AC), AN vuông góc với CE(N thuộc tia CE)
Chứng minh tam giác HAC đồng dạng với tam giác MEA và CD.CH+CE.CN=AC^2
Theo dõi (0) 1 Trả lời






